倾斜各向异性地层随钻电磁波响应模拟

范宜仁 李 虎 胡云云 孙庆涛

（1.中国石油大学地球科学与技术学院，山东 青岛 266580；2.中国石油大学（华东）CNPC测井重点实验室，山东 青岛 266580）

引 言

倾斜各向异性地层随钻电磁波响应数值模拟与特征分析，对基于随钻电测井资料进行实时地质导向与储层评价具有非常重要的意义［1-2］.目前，常用的随钻电磁波数值模拟方法包括:有限元法（Finite Element Method，FEM）［3-4］、有 限 差 分 法 （Finite Difference Method，FDM）［5-6］、传输线法（Transmission Line Matrix Method，TLM）［7］、数值模式匹配法（Numerical Mode Matching Method，NMM）［8］和快速傅里叶汉克尔变换结合的共轭梯度迭代法（Conjugate Gradient Method with Fast Fourier and Fast Hankel Transforms，CGFFHT）［9］.其中 FEM与FDM可以精细模拟随钻电磁波在任意倾角各向异性地层响应，但频域有限差分与有限元法都需要求解大型矩阵，计算过程复杂耗时；NMM 与CGFFHT求解相对较快，但无法实现对复杂仪器结构与地层模型的精细模拟.时域有限差分（Finite-Difference Time-Domain，FDTD）方法最早由 K.S.Yee1966年提出，该方法采用时间迭代的方法避免了大型稀疏矩阵的求解，能更好地适用于三维复杂介质随钻电磁波响应的模拟.本文采用柱坐标系FDTD实现了倾斜各向异性地层随钻电磁波响应模拟，并通过对不同地层条件下响应特征分析，理论研究了地层倾角、电导率各向异性、仪器发射频率等对随钻电磁波响应的影响.

1 方法原理

1.1 圆柱坐标系下各向异性电导率获取

随钻地层模型与仪器结构示意图如图1，假设地层层理方向与仪器轴线方向夹角为θ，则可以通过以下变换，将局部直角坐标系x′y′z′中电导率张量变换到与仪器轴重合的直角坐标系xyz下，有

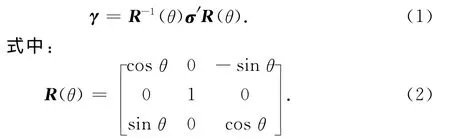
第二次旋转，将直角坐标系中电导率张量变换到圆柱坐标系ρφz下，本次变换可以表示为

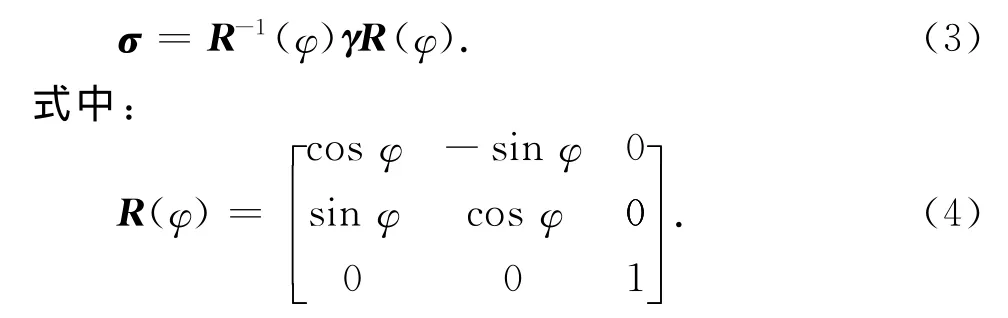
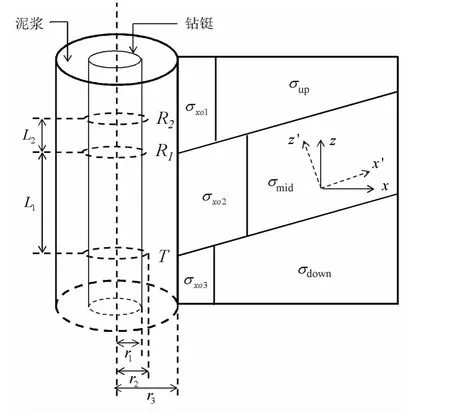
图1 随钻地层模型与仪器结构示意图

此时σ即为圆柱坐标系下电导率张量.

1.2 圆柱坐标系下各向异性地层FDTD差分格式

电性各向异性介质本构方程可表示为

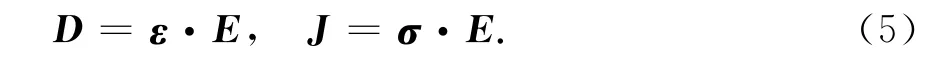
介质的磁性仍设为各向同性，即:

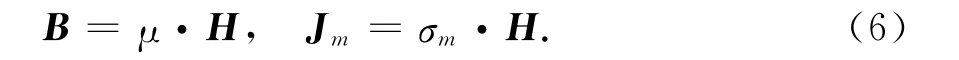
此时，Maxwell方程可表示为

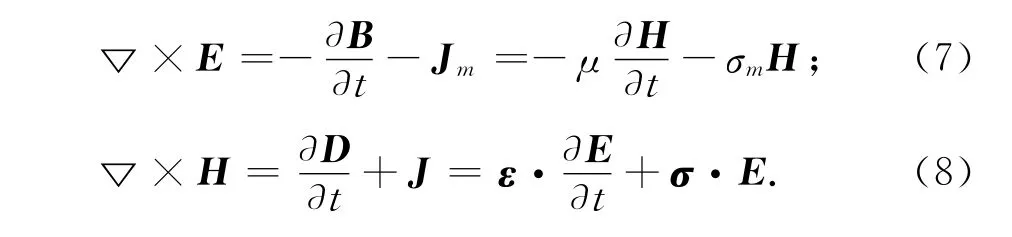
式（7）时域差分格式与各向同性时相同，即，

对式（8）进行离散得

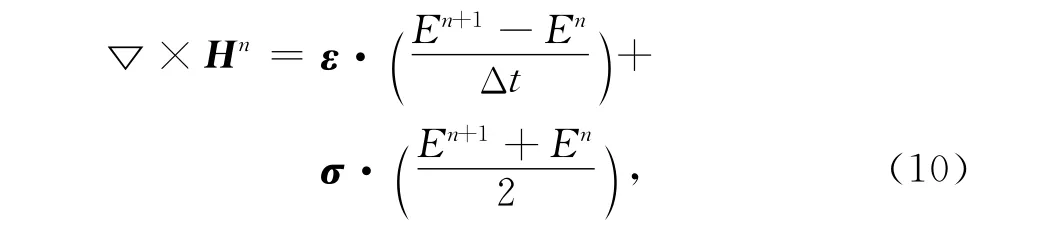
整理后得

1.3 介电常数放大策略

在磁导率为μ，介电常数为ε，电导率为σ的地层中，FDTD最大时间步长Δtc由空间步长决定，

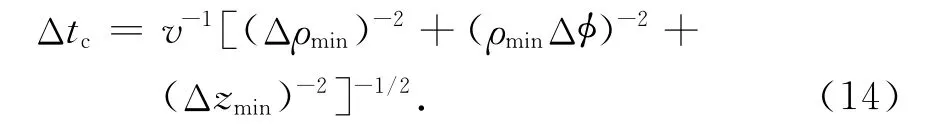
式中v为电磁波传播速度，

在随钻电磁波测井数值模拟过程中，由于位移电流远小于传导电流，可以通过放大介电常数增大时间步长.将式（8）重新整理为

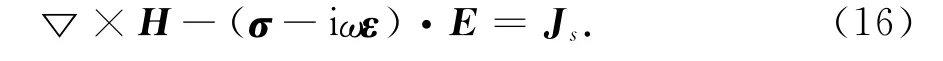
当σh（σv）＞＞ωε时，方程等效为

在模拟100kHz发射频率时，通过放大介电常数，计算需要时间可缩短80%，不同介电常数放大倍数下相位差、幅度比计算结果见图2，表1中给出了模型计算条件与CPU时间对比.

表1 不同介电常数放大倍数模型计算时间表

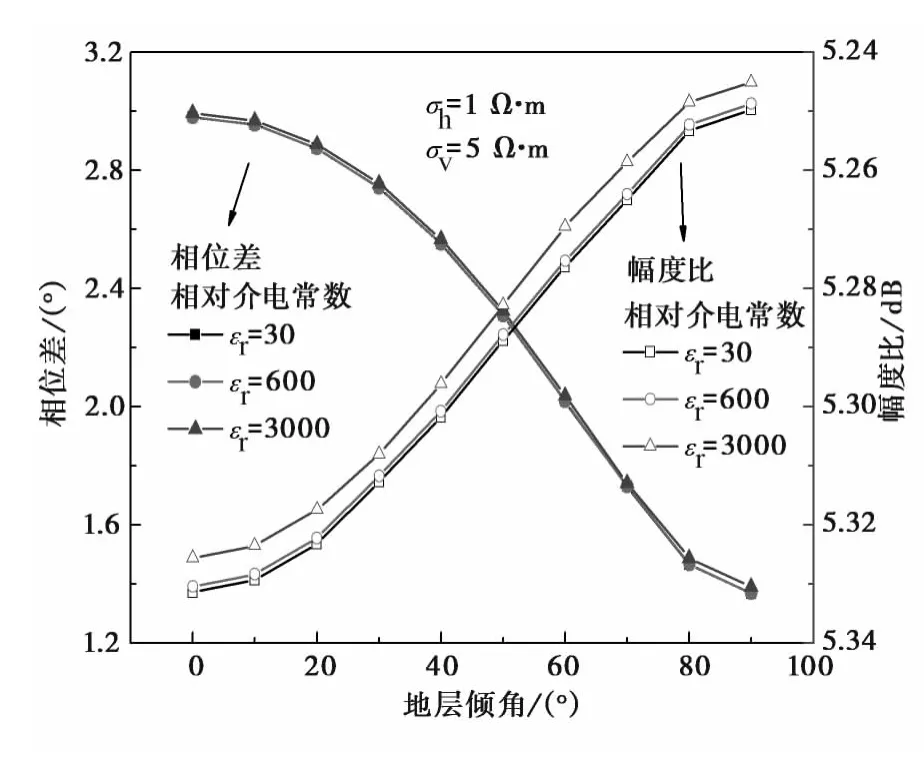
图2 介电常数放大策略效果图

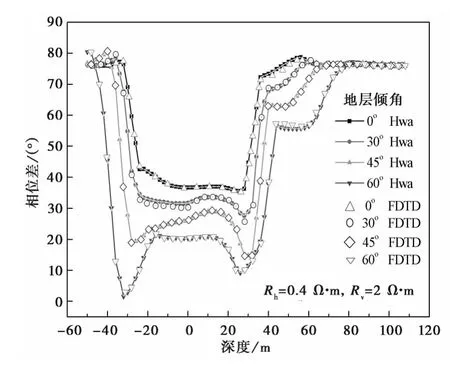
图3 模拟结果与文献［10］中Hwa计算结果对比

1.4 模拟结果验证

图3中给出了不同地层倾角条件下线圈距为［2430］in随钻电磁波相位差计算结果，并将计算结果与文献［10］中的结果进行对比，两者结果吻合很好，验证了算法的正确性.

2 各向异性地层随钻电磁波响应特征

实际测井过程中，通过对两接收线圈的相位差与幅度比进行刻度转化为相位／幅度电阻率，相位差（DP）与幅度比（RA）定义为

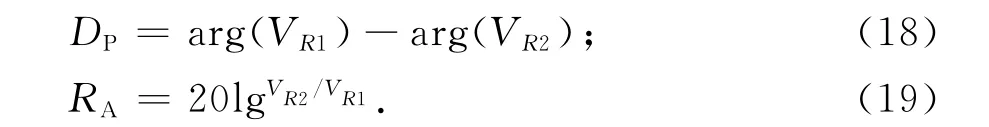
式中:V为接收线圈电位；arg为取相位角.对各向异性介质，定义各向异性系数

2.1 各向异性系数的影响

为了研究各向异性系数对相位（幅度）电阻率的影响，模拟了不同各向异性系数条件下倾斜地层随钻电磁波测井响应，模型中水平电阻率分别选取为1Ω·m、10Ω·m，模拟结果见图4.

地层倾角较小时（小于30°），不同水平电阻率条件下，各向异性系数对视电阻率影响较小，随地层倾角增大，各向异性系数对视电阻率影响增大，且地层水平电阻率越低，响应受地层各向异性影响越大，当地层倾角较大时，随各向异性系数增大，视电阻率甚至会超过垂直电阻率.

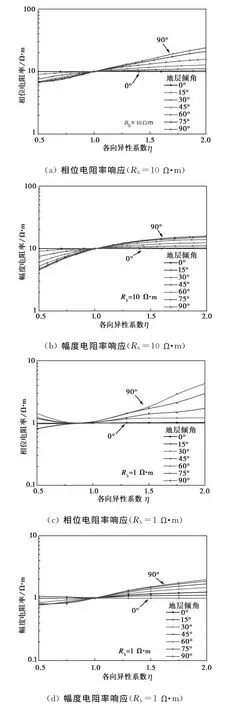
图4 不同各向异性系数条件下随钻电磁波测井响应

2.2 发射频率的影响

传统随钻电磁波仪器发射频率一般为500kHz与2MHz，新型的随钻方位电磁波增加了100kHz频率，为了研究不同发射频率对各向异性系数的敏感性，模拟了地层各向异性系数为，水平电阻率为0.5Ω·m时不同地层倾角条件下随钻电磁波响应（如图5），随发射频率增大，视电阻率受各向异性影响增强，当地层倾角较大时，2MHz频率下视电阻率甚至会远远超过垂直电阻率.

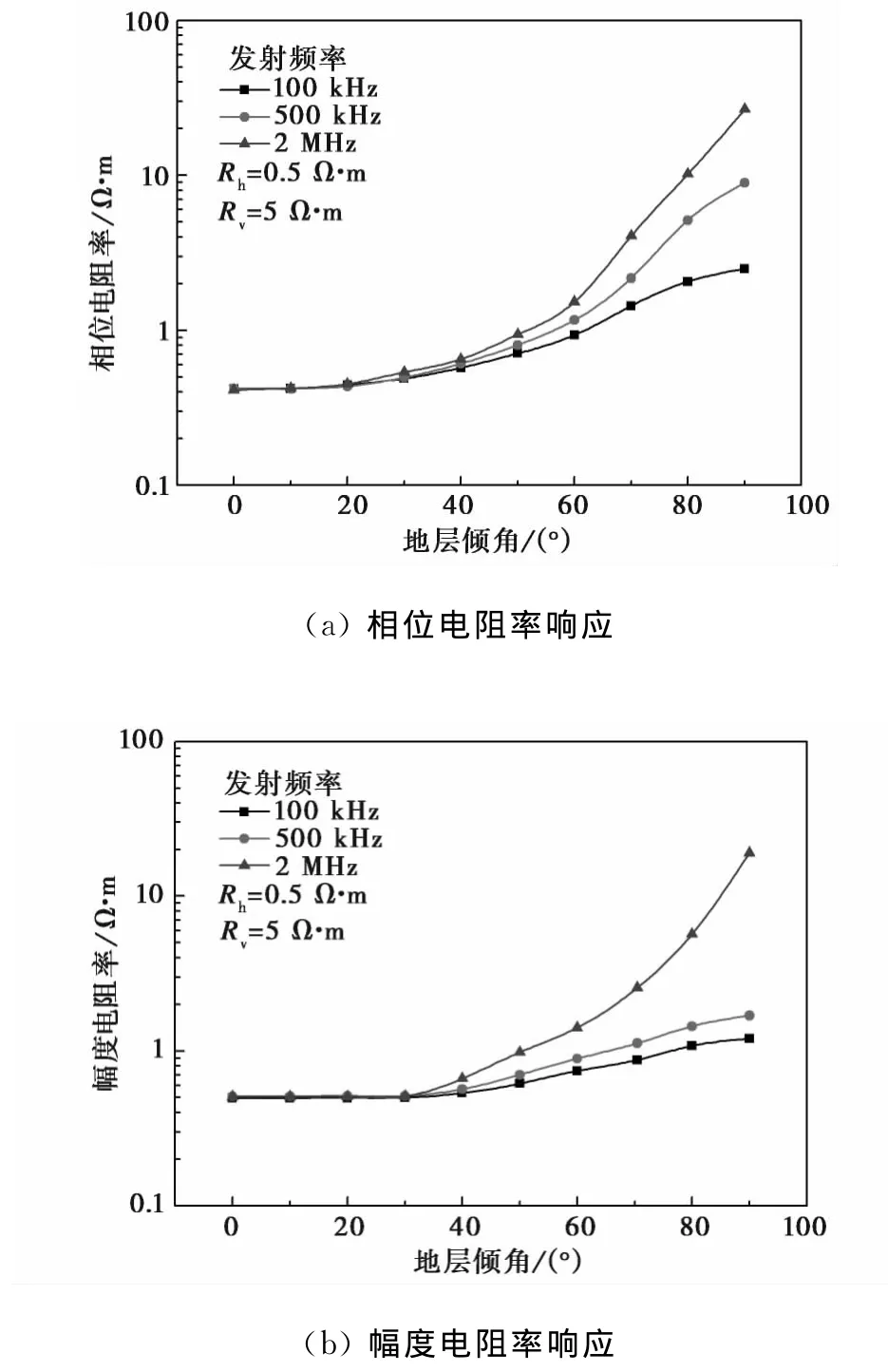
图5 不同发射频率条件下随钻电磁波测井响应

3 结 论

基于柱坐标系时域有限差分实现了倾斜各向异性地层随钻电磁波测井响应数值模拟，通过与已有结果对比，验证了算法的正确性.通过放大介电常数，在模拟100kHz发射频率时，计算时间可缩短80%.

地层倾角小于30°时，随钻电磁波视电阻率主要反映地层水平电阻率，地层倾角越大、发射频率越高，地层电阻率各向异性对视电阻率影响越大，且相位电阻率比幅度电阻率更加敏感，当发射频率较高、地层倾角较大时，随钻电磁波视电阻率甚至会远远超过地层垂直电阻率.

［1］ADERSON B，BONNET S，ROSTHAI R，et al.Response of 2MHz LWD resistivity and wireline induction tools in dipping beds and laminated［J］.J Log Analyst，1992，33（5）:461-475.

［2］BITTAR M S，HU G Y.The effects of rock anisotropy on LWD toroidal resistivity sensors［C／OL］／／SPWLA 46th Annual Logging Symposium，Noordwijk，The Netherlands，June 6-9，2004［2012-10-09］.http:／／www.spwla.org／publications／view／item／2785.

［3］CHANG S K，ANDERSON B.Simulation of induction logging by the finite-element method［J］.Geophysics，1984，49（11）:1943-1958.

［4］孙向阳，聂在平，李爱勇，等.用高阶叠层矢量有限元法计算随钻测井的三维电磁响应［J］.电波科学学报，2009，24（2）:273-279.SUN Xiangyang，NIE Zaiping，LI Aiyong，et al.The modeling of logging-while-drilling tool's threedimensional electromagnetic response using the high order hierarchical vector finite element method［J］.Chinese Journal of Radio Science，2009，24（2）:273-279.（in Chinese）

［5］HOLLAND R.Finite-difference time-domain（FDTD）analysis of magnetic diffusion［J］.IEEE Trans on Electromagnetic Compatibility，1994，36（1）:32-39.

［6］YEE K S.Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media［J］.IEEE Trans on Antennas and Propagation，1966，14（3）:302-307.

［7］LI J，CE L.A three-dimensional transmission line matrix（TLM）method for simulations of logging tools［J］.IEEE Transaction on Geoscience and Remote Sensing，2000，38（4）:1522-1529.

［8］LIU Q H，CHEW W C，TAHERIAN M R，et al.A modeling study of electromagnetic propagation tool in complicated borehole environments［J］.Log Analyst，1989，30（6）:424-436.

［9］ZHANG Z Q，LIU Q H.Simulation of induction logging response using conjugate gradient method with non-uniform fast Fourier and fast Hankel transforms［J］.Radio Science，2001，36（4）:59-608.

［10］LEE H O，TEIXEIRA F L.Cylindrical FDTD analysis of LWD tools through anisotropic dipping layered earth media［J］.IEEE Transaction Geoscience and Remote Sensing，2007，45（2）:383-388.