地-井时域激电拟牛顿法反演问题研究

潘和平 孟庆鑫

(1.中国地质大学地球物理与空间信息学院，湖北 武汉 430074；2.石家庄经济学院勘查技术与工程学院，河北 石家庄 050031)

引 言

井中激电地表-井中工作方式(地-井(Induced Polarization method,IP)IP)可实现多方位供电观测，接收装备置于井下接近矿体，获得异常较大，对钻孔地况要求低，工作效率高，观测信息较之井中直流电阻率法(井中Direct Current Resistivity method,DC)更丰富，解释判断方法原理直观简便，是金属矿普查或危机矿山勘探工作中重要的井中物探方法，取得了较好的应用效果[1-3].

井中DC/IP反演研究主要针对地面及井-地测量方式，Li等[4]针对地面与井中观测激电数据进行三维反演研究，Weller等[5]研究了激电数据的三维反演问题，Zhou等[6]完成了钻孔电阻率快速成像，Wilkinson等[7]研究了矿井电阻率成像问题；国内相关反演研究也取得了很大成果，阮百尧等[8]、吴小平等[9]分别研究了地面观测方式下的激电与电阻率法的反演技术，吕玉增等[10]、沈平等[11]研究了井间电阻率成像问题，岳建华等[12]、安然等[13]进行了井-地电阻率法成像研究.对于地-井激电的反演，由于观测数据量少，很难进行成像反演，主要采用切线法、正演拟合法等，来确定埋深、距井距离等参数以判断矿体方位等[14].

本文应用有限差分法和解析式法模拟三维地电模型中地-井激电方位测量的异常响应，基于正演模拟，采用理论解析式建立反演目标函数，利用最优化拟牛顿法[15-16]反演目标体方位等参数.

1 地-井时域激电三维正演

1.1 解析法与数值模拟法

正演是反演的基础，时域激电正演模拟主要由解析法和数值模拟法实现.解析法是针对球体、椭球体等规则形体，通过数学解法推导出电场分布情况，结果精确严格，一般作为理论解和参考比对依据[1].数值模拟利用数值方法对描述地球物理现象的偏微分方程及相应的边界条件进行近似求解模拟，适用性强效率高.黄智辉等[17]应用解析法对极化椭球体的地-井测量情况进行了阐述，文献[18]和[19]分别采用有限差分法和有限元法对地-井IP进行正演模拟并阐述分析了其异常特征；聂在平等[20-21]应用有限元法进行了井中电磁响应数值模拟研究.

本文正演主要基于有限差分法，以等效电阻率原理为出发点，采用解析解与数值解相结合的方式对三维地电模型的地-井IP进行正演模拟，正演所涉及的稀疏矩阵方程计算选用稳定双共轭梯度法[22]，减少迭代次数提高了效率.离散差分方程的推导过程及截断边界条件处理方法见文献[23]，本文仅列出稳流电场在求解三维区域内的七点差分格式

(1)

式中：

ao-1，p，q=(σo-1，p，q+σo，p，q)/[(Δxo+Δxo-1)Δxo-1]；

ao，p-1，q=(σo，p-1，q+σo，p，q)/[(Δyp+Δyp-1)Δyp-1]；

ao，p，q-1=(σo，p，q-1+σo，p，q)/[(Δzq+Δzq-1)Δzq-1]；

ao+1，p，q=(σo+1，p，q+σo，p，q)/[(Δxo+Δxo-1)Δxo]；

ao，p+1，q=(σo，p+1，q+σo，p，q)/[(Δyp+Δyp-1)Δyp]；

ao，p，q+1=(σo，p，q+1+σo，p，q)/[(Δzq+Δzq-1)Δzq]；

ao，p，q=-[ao-1，p，q+ao+1，p，q+ao，p-1，q+ao，p+1，q+

ao，p，q-1+ao，p，q+1]；

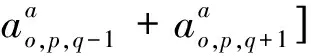
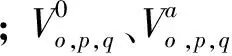
此外，本文还采用了稳定点电流场下井旁球状极化体的解析式作为有限差分模拟的参考依据和反演工作中的正演计算，其表达式可见文献[1].

1.2 实际算例与地-井时域IP异常的一般特征规律

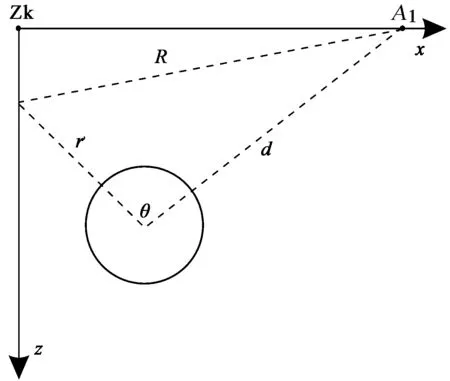
如图1(a)所示，缩小比例模型取均匀三维网格剖分，由离散网格节点上的电性值代替整个连续地电模型，中心垂直虚线为垂直钻孔，A0、A1、A2、A3、A4分别为场源布设于井口方位、主方位、反方位和两个辅助方位，虚线立方体表示井旁异常体.

算例1地电模型如图1(b)所示，无极化均质大地电阻率100 Ω·m，尺寸100 m×100 m×100 m

(a)

(b)

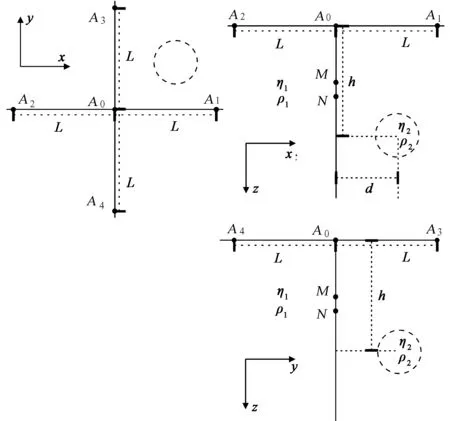
(c)图1 三维地电模型示意图

(三维网格剖分数101×101×101)；井旁直径8 m极化球体，球心坐标(x=9 m，y=0 m，z=-39 m)，电阻率10 Ω·m，极化率50%；场源位于A1方位坐标(x=11 m，y=0 m，z=0 m)，电流强度20 A；井Zk平面坐标(x=0 m，y=0 m).

由图2正演模拟结果对比可知：有限差分解所得曲线形态、数据结果都与解析解极为近似，显示出有限差分法在地-井IP模拟方面的适用性和准确性；但模拟计算中仍存在误差，这是因为有限差分只是利用有限的离散节点代替连续空间模型，误差会随测点接近异常体而逐步变大，但考虑到电位差的数值大小，这种误差是允许的.

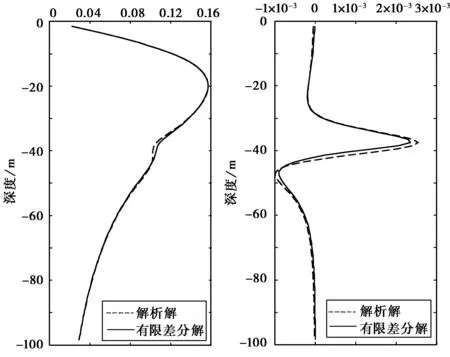
(a) 一次场电位差/V (b) 二次场电位差/V图2 有限差分解与解析解对比图

算例2地电模型如图1(c)所示，钻孔位于原点(0 m，0 m，0 m)，无极化均质大地电阻率100 Ω·m；井旁有一极化立方低阻体，边长8 m，中心坐标(8 m，3 m，-28 m)；五方位测量方式各方位长度L=20 m；接收电极MN距均为1 m.

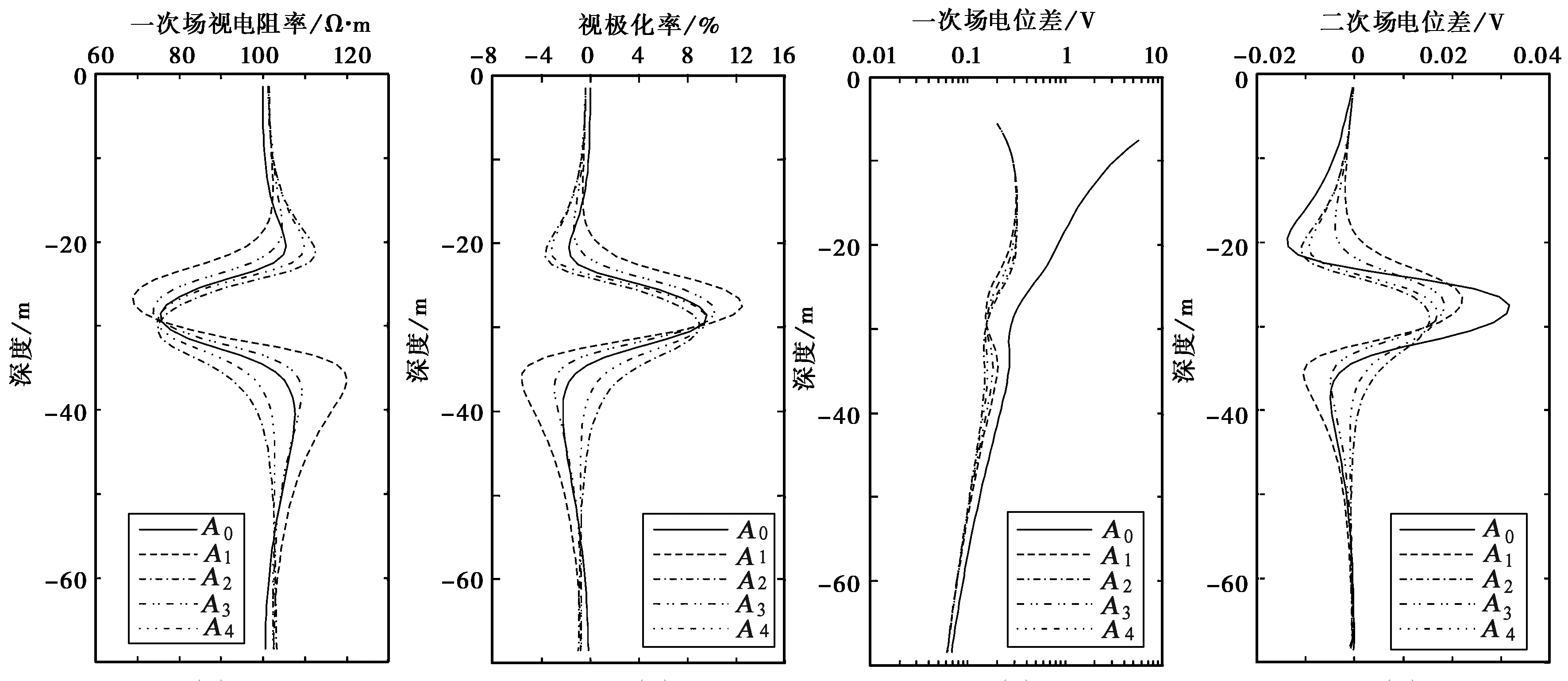
(a) (b) (c) (d)图3 井旁低阻极化立方体有限差分正演模拟结果

正演结果如图3所示：各方位的视电阻率极小值和视极化率极大值大致都在靠近异常体中心深度的观测位置上；并因激发方位差异，异常曲线出现不同特征(各方位曲线特征与文献[19]利用有限元法模拟结果相近).分析二次场电位差可知各方位测量曲线形态与视极化率曲线相近，但对于该地电模型，井口方位所测二次场幅值最大，显示出不同方位对于异常体不同的极化效果[1，17].总之，不同方位的激电测量结果差别明显，可用来推断目标体位置等信息；视电阻率和一次场电位差主要反应场源对异常体的激发情况，视极化率和二次场电位差主要反应场源对异常体的极化情况.

2 拟牛顿最优化反演方法

本节基于前文正演模拟中对地-井IP测量特征的认识，采用稳流电场中规则形体解析式进行反演目标函数和偏导数矩阵的构建，应用拟牛顿法建立最优化拟合反演方法.

2.1 反演基本思路

首先基于最小二乘原则建立反演目标函数[16]

(2)

本文以极化球体为例，选取其理论解析式作为目标函数，均匀无极化介质中井旁球体极化场电位解析式见文献[1].经试算可知：虽然极化球体解析式涉及不同系数的高次勒让德多项式，但可用少数几个多项式近似代替；目标函数可视为一个多变量高次函数，基于此的反演工作也就相当于在限定条件下利用最优化法求解一个多变量的高次函数.

2.2 共轭梯度法与变尺度法

牛顿法优点是收敛速度快，但需要计算Hessian阵(H)的逆矩阵H-1，为此研究者采用共轭梯度法和变尺度法对其进行了改进.两种方法都是选择一个拟矩阵，使其尽可能近似于H-1，避免直接求取逆矩阵[24].

共轭梯度(Conjugate Gradient，CG)法的基本原理是将共轭性和梯度法相结合，利用所求模型参数向量在已知迭代点上的梯度方向形成一系列线性无关彼此成H共轭的向量ρM，并沿该方向进行搜索，形成每次迭代递推格式，求出目标函数的极小点，获取所求模型参数的最优化解.其迭代式可写为

v(M)=v(1)+β1ρ1+β2ρ2+…+βM-1ρM-1.

(3)

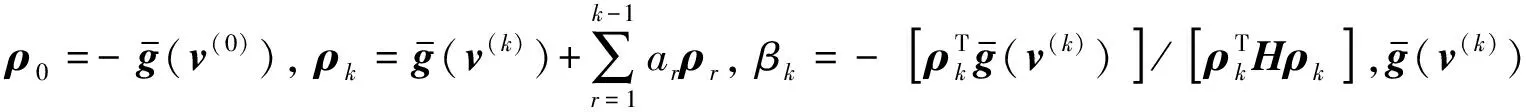
CG法仍要计算Hessian阵，研究者提出许多变种算法，其中较简便的如Fletcher-Reeves(FR)法，根据式(4)将基本共轭法进一步简化为FRCG法[25].

(4)

(5)

(6)

(7)

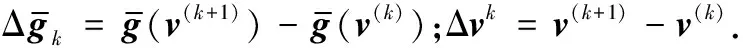
2.3 具体反演方法

本文的反演试算采用FRCG法(Fletcher-Reeves Conjugate-Gradient)和BFGS法(Boyden-Fletcher-Goldfarb-Shanno)，观测数据为地-井IP方位(选取主、反、两个辅助方位)测量的一次场电位差和极化场电位差，分别对井旁异常体的一次场和极化场进行反演，待反演模型参数为：异常体电阻率(极化电阻率ρ*或一次场电阻率ρ2)，异常体中心坐标(xp，yp，zp)，球体半径a；即五个待求参数.最优化反演方法存在多解性，地-井IP所测数据量又较少，基于对地-井方位测量特征的认识，适当加入一定的限制条件对所要反演的参数向量进行约束，可使反演结果更精确.图4为FRCG和BFGS最优化反演流程图.

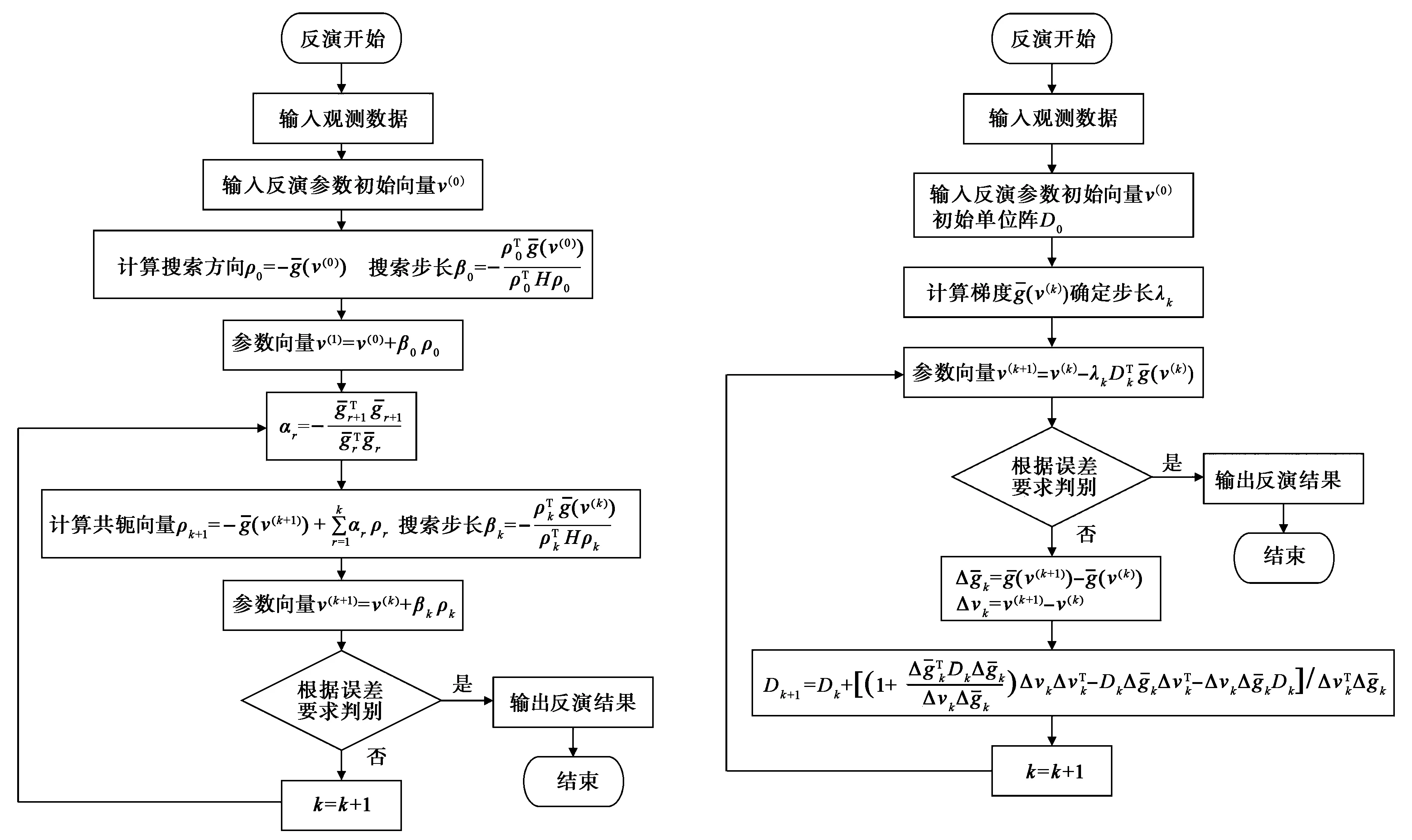
(a) FRCG最优化法反演程序框图 (b) BFGS最优化法反演程序框图图4 最优化法反演程序框图

3 反演算例与分析

本节应用拟牛顿最优化反演方法，对三维地电模型下井旁球体的方位、埋深等参数进行正演拟合反演，并对该方法的可行性和适用性进行简要分析.

3.1 试算算例

算例1如图1(c)所示，地电模型为非极化均质大地(电阻率100 Ω·m)；垂直井位于原点，井旁有一半径4 m的极化球体，中心坐标(xp=8 m，yp=7 m，zp=-15 m)，球体电阻率ρ2=10 Ω·m，极化率50%；五方位测量场源为A0、A1、A2、A3、A4，电流强度20 A，方位长度L=20 m.

地-井IP观测数据分别为一次场电位差和极化场电位差，由极化球体的解析式求解得出，并加入1%的随机噪音.应用最优化法进行反演，利用极化球体解析式进行正演计算，分别对一次场和极化场电位差数据进行反演.

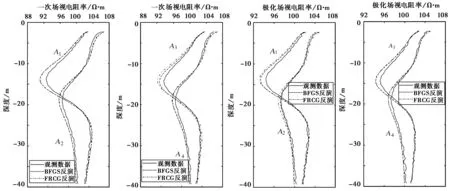
(a) 主剖面 (b) 辅助剖面 (c) 主剖面 (d) 辅助剖面图5 最优化反演拟合结果

反演初始模型参数为：球心坐标(xp=4 m，yp=4 m，zp=-5 m)，ρ2=20 Ω·m，ρ*=30 Ω·m，a=2 m.反演拟合结果如图5所示.

应用BFGS法进行反演(迭代次数20)，一次场各参数反演结果：ρ2=10.325 Ω·m，a=4.329 m，中心坐标为(xp=7.992 m，yp=7.091 m，zp=-14.838 m)； 极化总场各参数反演结果：ρ*=20.807 Ω·m，a=4.281 m，中心坐标为(xp=8.101 m，yp=7.130 m，zp=-14.937 m).

应用FRCG法进行反演(迭代次数20)，一次场各参数反演结果：ρ2=10.441 Ω·m，a=4.294 m，中心坐标为(xp=8.209 m，yp=7.056 m，zp=-14.931 m)；极化总场各参数反演结果：ρ*=20.750 Ω·m，a=4.321 m，中心坐标为(xp=8.223 m，yp=7.103 m，zp=-14.815 m).

算例2仍采用图1(c)所示地电模型，地-井IP五方位观测数据由有限差分法进行正演计算(地电模型为40 m×40 m×40 m，网格节点为81×81×81)得出，分别为一次场电位差和极化场电位差，并同样基于有限差分正演计算进行反演，模型参数与前同.由于是均匀网格节点组成，每次反演所得方位数据均转化在与之最近的网格节点上.

反演初始模型参数为：球心坐标(xp=4 m，yp=4 m，zp=-5 m)，ρ2=15 Ω·m，ρ*=30 Ω·m，a=3 m.反演拟合结果如图6所示.

(a) 主剖面 (b) 辅助剖面 (c) 主剖面 (d) 辅助剖面图6 最优化反演拟合结果

应用BFGS法进行反演(迭代次数6)，一次场各参数反演结果：a=4.5 m，ρ2=10.95 Ω·m，中心坐标为(xp=8 m，yp=7.5 m，zp=-13.5 m)；极化总场反演结果：ρ*=21.62 Ω·m，a=4.5 m，中心坐标为(xp=8 m，yp=7.5 m，zp=-14 m).

应用FRCG法进行反演(迭代次数6)，一次场各参数反演结果：a=4.5 m，ρ2=11.41 Ω·m，中心坐标为(xp=8 m，yp=7.5 m，zp=-13.5 m)；极化总场参数反演结果：ρ*=20.96 Ω·m，a=4.5 m，中心坐标为(xp=8.5 m，yp=7 m，zp=-14 m).需要说明，反演结果都是小数，而求解区域为均匀网格剖分，坐标点和球体半径参数都变为与之最邻近的节点数值，在数值上都根据剖分情况有所取舍，于是造成两种拟牛顿方法反演结果近似，反演拟合数据曲线几乎重合，实际上各个参数计算结果都略有差别.

3.2 算例分析

从上述算例反演拟合情况来看，所得曲线趋势和观测值保持一致，拟合效果较为理想，同时对待求参数的反演结果也与模型设定较为接近，说明本文选取反演方法可达到较好的拟合效果，具有一定的适用性；同时具体反演参数结果和所设模型仍有一定差别，因为最优化法的多解性，在所选限定条件内，还有能达到相近结果的参数组合；经过试算，适当加入限定条件，反演参数结果可进一步优化.

4 结 论

本文利用有限差分法，以极化球体解析式为比对，对三维地电模型中地-井时域激电异常特征进行了正演模拟；应用共轭法、变尺度最优化法进行了基于解析法正演与有限差分正演的反演研究，获得了如下结论和认识：

应用拟牛顿法(BFGS法、FRCG法)，在适当的限定条件下，利用地-井激电方位测量数据，对井旁规则形体或类似规则形体进行多参数的最优化反演是可行的，获得的反演结果较好，拟合精度较高.

拟牛顿最优化反演法拥有较好的收敛性，具有一定的适用性，但对于反演初值设定要求较高，在进行反演工作时按情况选取较为接近结果的数据可以在保证拟合精度的前提下减少反演迭代次数.

实际地质条件下的井旁目标体往往不是规则形体，电性和大小等参数也难以加入合适的限定条件，故需研究适用性更广的解释模型；此外，多参数反演较为复杂，各个待求参数对整个观测数据的影响有较大差异，对此进行研究可进一步提高改进反演方法技术；考虑到实际工作中地质情况较复杂，应适当采取人机互动的方式进行拟合反演.

[1] 蔡柏林，黄智辉，谷守民.井中激发极化法[M].北京:地质出版社，1983．

[2] STEPHEN T，MUDGE.Radial resistivity/IP surveys using a down-hole current electrode[J].Exploration Geophysics，2004，35:188-193．

[3] 高长荣.井中激电在西霞矿区的应用[J].物探与化探，2007，31(S1):98-101．

GAO Changrong.The application of the borehole IP method in the XiXia ore district[J].Geophysical & Geochemical Exploration.2007，31(S1):98-101.(in Chinese)

[4] LI Y G，OLDENBURG D W.3-D inversion of induced polarization data[J].Geophysics，2000，65(6):1931-1945．

[5] WELLER A，FRANGOS W，SEICHTER M.3-D inversion of IP data from simulated waste[J].Journal of Applied Geophysics，2000，44:67-83．

[6] ZHOU B，GREENHALGH S A.Rapid 2D/3D crosshole resistivity imaging using the analytic sensitivity function[J].Geophysics，2002，67(2):755-765．

[7] WILKINSON P B，CHAMBERS J E，et al.Extreme sensitivity of crosshole electrial resistivity tomography measurements to geometric errors[J].Geophy J Int，2008，173:49-62．

[8] 阮百尧，村上裕，徐世浙.激发极化数据的最小二乘二维反演方法[J].地球科学，1999，24(6):619-624．

RUAN Baiyao，YUTAKA M，XU Shizhe.Least square 2-D inversion method for induced polarization data[J].Geophysical & Geochemical Exploration,1999，24(6):619-624.(in Chinese)

[9] 吴小平，徐果明.利用共轭梯度法的电阻率三维反演研究[J].地球物理学报，2000，43(3):420-427．

WU Xiaoping，XU Guoming.Study on 3-D resistivity inversion using conjugate gradient method[J].Chinese J Geophys，2000，43(3):420-470.(in Chinese)

[10] 吕玉增，阮百尧，黄俊革.直流电井间三维直接成像[J].物探化探计算技术，2003，25(1):60-64．

LV Yuzeng，RUAN Baiyao，HUANG Junge.The 3-D immediate corsshole tomography with direct current[J].Computing Techniques for Geophysical & Geochemical Exploration.2003，25(1):60-64.(in Chinese)

[11] 沈 平，强建科，李永军，等.井间视电阻率的几何成像方法[J].中南大学学报:自然科学版，2010，41(3):1079-1084．

SHEN Ping，QIANG Jianke，LI Yongjun，et al. Geometry image method of crosshole apparent resistivity[J].Journal of Central South University:Science and Technology，2010，41(3):1079-1084.(in Chinese)

[12] 岳建华，刘志新.井-地三维电阻率成像技术[J].地球物理学进展，2005，20(2):407-411．

YUE Jianhua，LIU Zhixin.Three dimension resistivity tomography of mine ground[J].Progress in Geophysics，2005，20(2):407-411.(in Chinese)

[13] 安 然，李桐林，徐凯军.井-地三维电阻率反演研究[J].地球物理学进展，2007，22(1):247-249．

AN Ran，LI Tonglin，XU Kaijun.Well-surface 3-D resistivity inversion[J].Progress in Geophysics，2007，22(1):247-249.(in Chinese)

[14] 周 峰，潘和平，吴国平，等.井中激电地-井方式井旁球体正反演.物探与化探，2008，32(3):321-325．

ZHOU Feng，PAN Heping，WU Guoping，et al.Forward and inversion of sphere beside well in then method of ground-well induced polarization[J].Geophysical & Geochemical Exploration，2008，32(2):321-325.(in Chinese)

[15] 潘和平，黄智辉.岩性和煤质最优化变尺度法分析[J].物探与化探，1991，15(3):168-173．

PAN Heping，HUANG Zhihui.Analysis of lithology and coal quality with the optimized scale transformation method[J].Geophysical & Geochemical Exploration，1991，15(3):168-173.(in Chinese)

[16] 潘和平，马火林，蔡柏林，等.地球物理测井与井中物探[M].北京:科学出版社，2009．

[17]黄智辉.井中激电地-井方式方位测量资料解释问题的探讨[J].物探与化探，1979，3(3):22-30．

HUANG Zhihui.Discussion on data interpretation of azimuth measurement in the surface-hole mode of IP borehole[J].Geophysical & Geochemical Exploration.1979，3(3):22-30.(in Chinese)

[18] 周 峰，潘和平，文国军，等.基于有限差分的井中激发极化法正演[J].电波科学学报，2010，25(4):785-791．

ZHOU Feng，PAN Heping，WEN Guojun，et al.Three-dimensional forward modeling of induced of polartization borehole using finite difference method[J].Chinese Journal of Radio Science，2010，25(4):785-791.(in Chinese)

[19] 吕玉增，阮百尧，彭苏萍.地-井方位激电观测异常特征研究[J].地球物理学进展，2012，27(1):201-216．

LÜ Yuzeng，RUAN Baiyao，PENG Suping.A study on anomaly of surface-borehole direction induced polarization survey[J].Progress in Geophysics，2012，27(1):201-216.(in Chinese)

[20] 孙向阳，聂在平，李爱勇，等.用于电磁感应建模的一种快速有效计算方法[J].电波科学学报，2008，23(5):932-936．

SUN Xiangyang，NIE Zaiping，LI Aiyong，et al.A fast and effective computational method of modeling the electromagnetic induction[J].Chinese Journal of Radio Science，2008，23(5):932-936.(in Chinese)

[21] 孙向阳，聂在平，李爱勇，等.用高阶叠层有限元法计算随钻测井的三维电磁响应[J].电波科学学报，2009，24(2):273-279．

SUN Xiangyang，NIE Zaiping，LI Aiyong，et al.The modeling of logging while drilling tool’s 3-D electromagnetic response using the high order hierarchical vector finite element method[J].Chinese Journal of Radio Science，2009，24(2):273-279.(in Chinese)

[22] 吴建平，王正华，李晓梅.稀疏线性方程组的高效求解与并行计算[M].长沙：湖南科技出版社，2004．

[23] 罗延钟，张桂青.电子计算机在电法勘探中的应用[M].武汉:武汉地质学院出版社，1987．

[24] 王家映.地球物理反演理论[M].北京:高等教育出版社，2002．

[25] 袁亚湘，孙文瑜.最优化理论与方法[M].2版.北京：科学出版社，1997．