分布式电磁矢量传感器阵的二维测向算法
邵 华 苏卫民 顾 红 樊劲宇
(南京理工大学电子工程与光电技术学院,江苏 南京 210094)
引 言
电磁矢量传感器是由相位中心重合的三个正交电偶和三个正交的磁偶组成[1-2].与标量传感器相比[3-5],它能同时获得目标的空间和极化角度信息.因此,为了提高测向精度,人们把它应用于信号源的二维波达角2-D DOA估计中,并且已经发展了许多有效的2-D DOA估计算法[1-2,4-8].然而,这些算法中的大多数,例如旋转不变因子(Estimating Signal Parameters Viarotational Invariance Techniques,ESPRIT)算法[7]和传播因子(Propagator Method,PM)算法[8],都采用了独立信号源的假设条件.这使得它们并不适用于多路径环境下的相干信号源的角度估计.
针对基于电磁矢量阵的相干信号2-D DOA估计问题,文献[9]提出了一种不损失阵列孔径的极化平滑(Polarization Smoothing Algorithm,PSA)算法,并结合相应算法进行2-D DOA估计.文献[10]给出了一种极化差平滑算法(Polarization Difference Smoothing Algorithm,PDSA),它是文献[11]应用于色噪声的一种扩展去相干技术.尽管如此,这两种算法在去除信号相关性的同时都损失了电磁矢量传感器的向量特性.这导致阵元间距不能大于入射信号的半波长,可处理信号的最大个数也受限于矢量传感器的分量数.文献[11]讨论了一种将平面加孤立阵的几何结构应用于电磁矢量传感器中的2-D DOA估计算法.文献[12]研究了一种基于均匀线性极化敏感阵列的新型极化平滑算法(uniform linear array polarization smoothing algorithm, ULAPSA).虽然文献[11-12]都避免了向量特性的损失,但是文献[11]要求2-D空间平滑,文献[12]采用的电磁矢量传感器的各分量具有共点结构,使得其只能沿线阵的基线方向进行阵列孔径扩展.
针对以上问题,我们设计了一种由分布式电磁矢量传感器组成的稀疏线阵,其中分布式电磁矢量传感器包括沿y轴分布的三个正交的电偶和三个正交的磁偶,并假设其分布间距远大于半波长,它不同于文献[13-14]中建议的电磁矢量传感器各分量的位置分布.这种几何结构使得分布式电磁矢量传感器不但具有电磁矢量传感器的向量特性,而且包含了沿y轴的空间相位因子.进一步假定上述线阵沿x轴放置并且其阵元间距远大于半波长,那么整个线阵除了包含上述特性外还具有沿x轴的空间相位因子.为充分利用稀疏线阵的这些特点,提出了一种基于扩展孔径的相干信号2-D DOA估计算法.首先,通过构造增强矩阵来去除信号的相关性;其次,利用矢量传感器的向量特性获得低精度无模糊的方向余弦估计;然后,根据沿x轴和y轴的空间相位因子来获得高精度模糊的方向余弦估计;最后以低精度方向余弦估计为参考,去除高精度方向余弦估计的周期性模糊,从而实现高精度无模糊的2-D DOA估计.与传统相干信号2-D DOA算法相比,本文算法具有以下优势:1)不破坏电磁矢量传感器的向量特性;2)分布式电磁矢量传感器的引入给1维稀疏线阵带来2维孔径扩展.仿真结果表明本文算法能提供更好的测向性能.
1 信号模型
假设K个窄带远场极化相干信号分别从(θ1,φ1),…,(θK,φK)角度入射到如图1所示的线阵上,其中0≤θk<π/2和0≤φk<2π分别表示俯仰角和方位角.该线阵是由M个分布式电磁矢量传感器组成并沿x轴以间距Δx均匀排列,其中分布式电磁矢量传感器的三个正交电偶和三个正交磁偶沿y轴相距Δy.令Δx≫λ/2和Δy≫λ/2,其中λ表示入射信号波长.类似于电磁矢量传感器导向矢量模型[6-7],对每个分布式电磁矢量传感器,第k个入射信号的6×1维导向矢量为
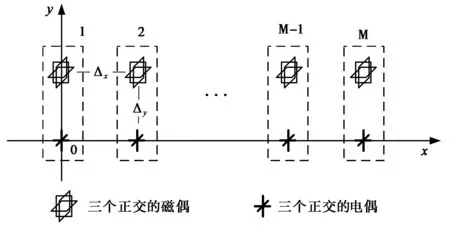
图1 由分布式电磁矢量传感器组成的稀疏线阵
ck
(1)
式中:qy,kexp(j2πΔyvk/λ)表示第k个信号的y轴空间相位因子,vkcosθksinφk表示第k个信号的y轴方向余弦;0≤γk<π/2和-π≤ηk<π为第k个入射信号的极化参数;(·)T表示矩阵转置.以第1个传感器为参考,那么第m个传感器对第k个信号的空间相位因子为其中ukcosθkcosφk表示第k个信号的x轴方向余弦.那么对所有K个入射信号,第m个传感器在t时刻的接收信号矢量为
m=1,…,M.
(2)
式中:sk(t)表示第k个信号包络;nm(t)表示第m个传感器在t时刻的接收噪声,假设其服从零均值高斯白噪声分布,彼此相互独立,与信号也不相关.根据式(2),该线阵在t时刻6M×1维接收信号矢量为
y(t)=(C⊙Qx)βs1(t)+n(t).
(3)
式中:C[c1,…,cK];Qx[qx,1,…,qx,K],qx,k[β1,…,βK]T,βksk(t)/s1(t);n(t)⊗和⊙分别表示Kronecker积和Khatri-Rao积.采集T个快拍数,形成阵列接收数据矩阵Y=[y(t1),…,y(tT)].利用矩阵Y来求取高精度无模糊的2-D DOA估计.
2 算法描述
信号的相干性引起子空间类算法性能下降甚至失败,为此首先采用矩阵增强技术来消除信号的相干性.
2.1 矩阵增强去除信号相干性
改写向量y(t)以如下6×M维矩阵形式
(4)
式中:Βdiag{β1,…,βM};N(t)为6×M维噪声矩阵.将6×M维矩阵Z(t)分解成LM-K+1个6×K维子矩阵,M>2K,其中第l个子矩阵为
(5)
式中:Jl[0(l-1)×K,IK,0(L-l)×K]T;Qx,1利用上述L个子矩阵形成如下6L×K维增强矩阵
(6)
式中Nx(t)进行简单的行变换,增强矩阵X(t)可以重新写为
(7)
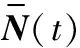
R
(8)
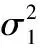
2.2 低精度无模糊的方向余弦估计
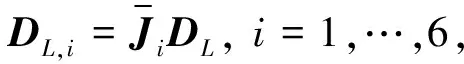
(9)
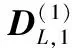

(10)
式中Λi是满秩矩阵,中各行都可以用来线性表示[12],即存在惟一的线性矩阵P使得
(11)
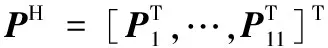
(12)
根据式(10)和式(12),可得
(13)
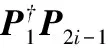
(14)
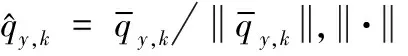
2.3 高精度模糊的方向余弦估计
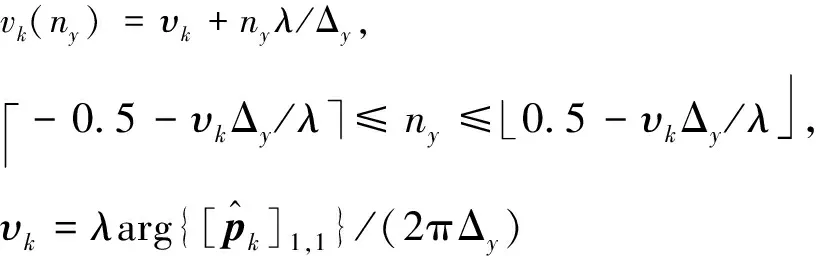
(15)
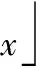
下面推导高精度模糊的x轴方向余弦估计.把DL对应的L个阵元的阵列分成两个重叠的子阵,每个子阵包含L-1个阵元,那么这两个子阵对应的6(L-1)×K维导向矩阵分别为
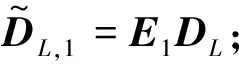
(16)

(17)
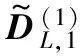
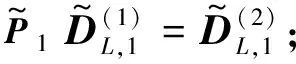
(18)
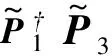
(19)
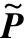
(20)
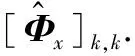
uk(nx)=μk+nxλ/Δx,
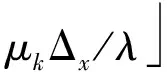
(21)
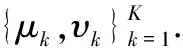
2.4 高精度无模糊的2-D DOA估计
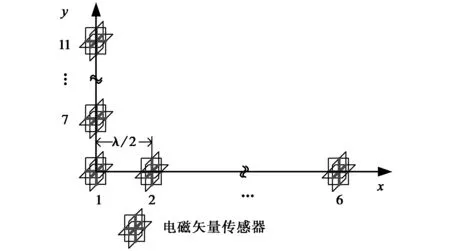
图2 由11个电磁矢量传感器组成的L型阵列
3 仿真试验及结果分析

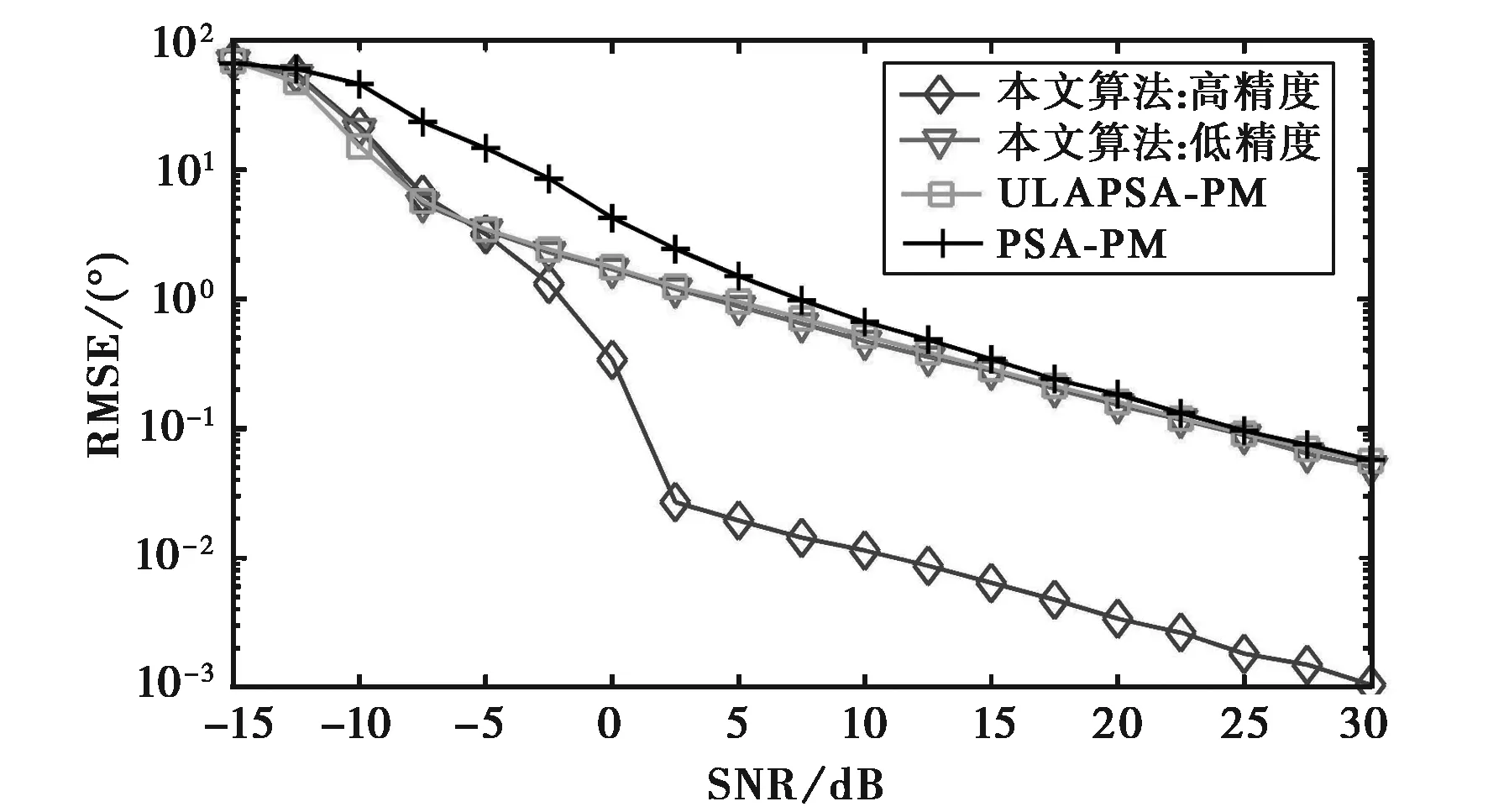
图3 RMSE随SNR的变化曲线
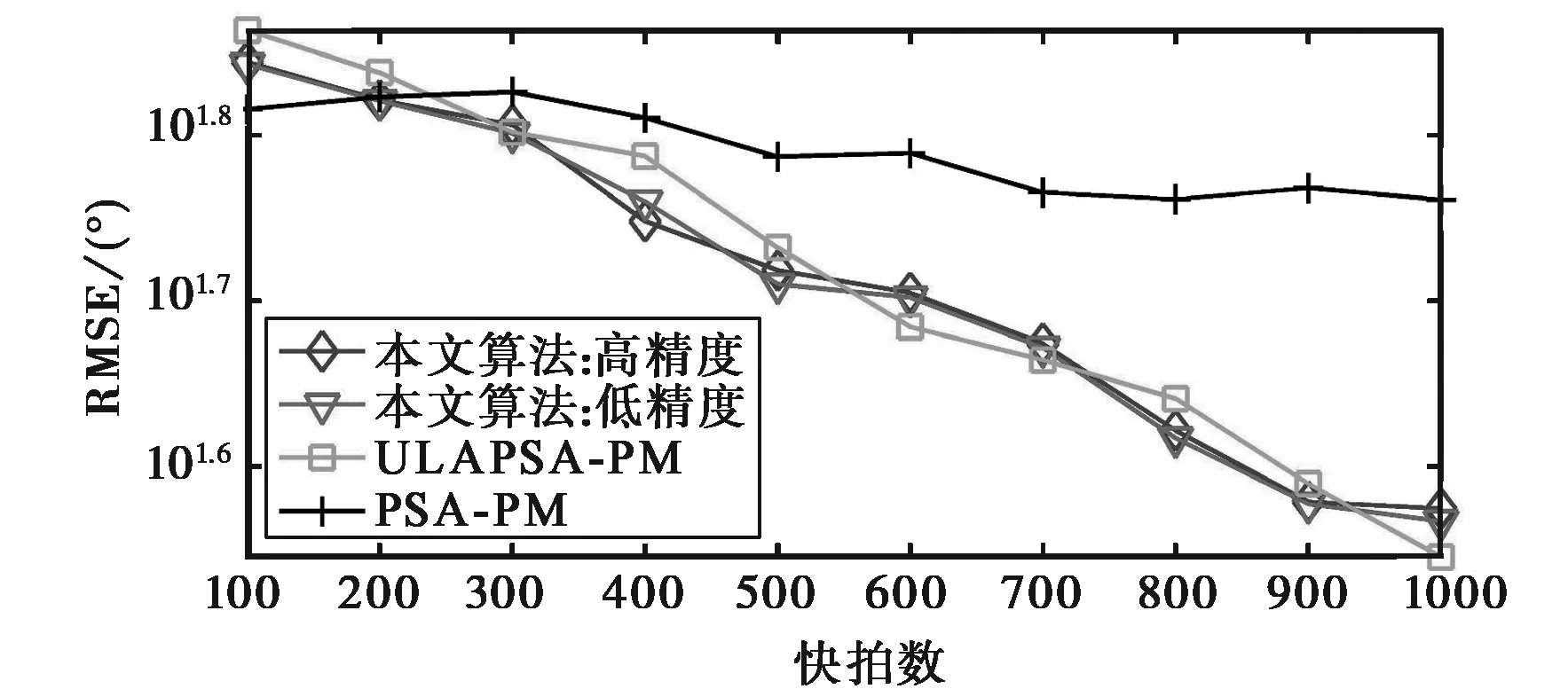
(a) RSN=-15 dB
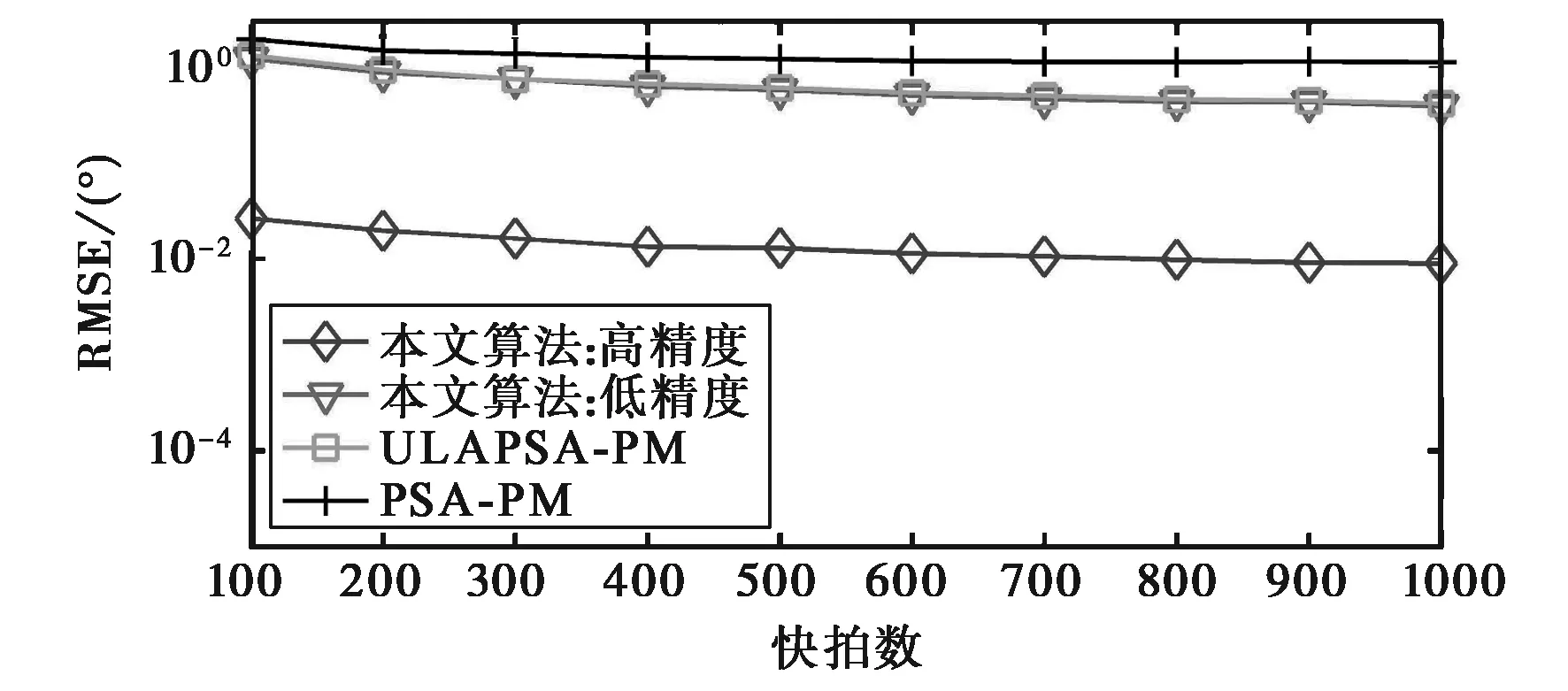
(b) RSN=5 dB图4 RMSE在不同SNR下随快拍数的变化曲线
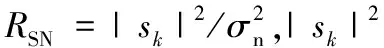
图4给出了信号1的2-D DOA估计的RMSE在不同SNR下随快拍数的变化曲线.图4表明当RSN=5 dB时高精度估计的RMSE明显小于其他两种算法;当SNR降为-15 dB时,本文算法的两种估计的RMSE均与ULAPSA-PM算法具有相近的数值.然而,在小快拍低信噪比的情况下,本文算法与ULAPSA-PM算法的RMSE都大于PSA-PM算法,这归因于前两种算法都使用了信号完全相干的假设(如式(4)),这在小快拍数下并不成立,因此它们的估计性能不如后者.
图5描绘了信号1的2-D DOA估计的RMSE随阵元间距的变化曲线.由于PSA-PM算法要求阵元间距小于0.5λ,所以并未参与图5中测向性能的比较.SNR和快拍数分别为10 dB和200.阵元间距的变化范围是[0.5λ,40.5λ].很明显,在[0.5λ,24.5λ]范围内,本文算法具有最好的测向性能,并且RMSE随阵元间距的增大而减小.尽管如此,阵元间距的扩大导致模糊数的增多,解模糊正确概率的减小.这使得本文算法高精度估计的性能在阵元间距大于24.5λ时急剧下降,最终与低精度估计具有近似的测向性能.
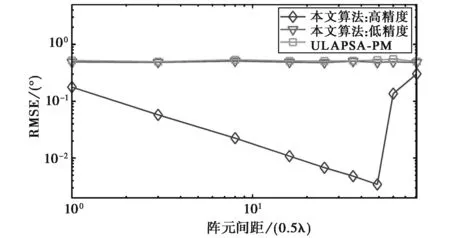
图5 RMSE随阵元间距的变化曲线
4 结 论
针对分布式电磁矢量传感器稀疏线阵,本文提出了一种基于扩展孔径的相干信号2-D DOA估计算法.与传统算法不同,该算法既保留了电磁矢量传感器的向量特性,又通过增大分布式电磁矢量传感器内部分量的间距以及传感器之间的间距来扩大阵列孔径,提高测向精度.仿真结果表明在硬件代价相同的情况下本文算法具有更低的测向误差.
[1] NEHORAI A,PALDI E.Vector-sensor array processing for electromagnetic source localization[J].IEEE Transactions on Signal Processing,1994,42(2):376-398.
[2] LI Jian.Direction and polarization estimation using arrays with small loops and short dipoles[J].IEEE Transactions on Antennas and Propagation,1993,41(3):379-387.
[3] 周 围,朱联祥,周正中,等.相干多径环境下信号空间特征及波达方向估计[J].电波科学学报,2007,22(4):685-690.
ZHOU Wei,ZHU Lianxiang,ZHOU Zhengzhong,et al.Estimation of spatial signature and direction of arrivals for signals in coherent multipath environment[J].Chinese Journal of Radio Science,2007,22(4):685-690.(in Chinese)
[4] 郑 植,李广军,腾云龙.基于双平行线阵的相干分布源二维DOA估计[J].电波科学学报,2010,25(6):1123-1129.
ZHENG Zhi,LI Guangjun,TENG Yunlong.Estimation of 2-D-DOA for coherently distributed sources with two parallel linear arrays[J].2010,25(6):1123-1129.(in Chinese)
[5] 邵 华,苏卫民,顾 红,等.基于稀疏互质L型阵列的二维测向算法[J].电波科学学报,2012,27(5):886-891.
SHAO Hua,SU Weimin,GU Hong,et al.Two-dimentional direction finding using a sparse coprime L-shaped array[J].Chinese Journal of Radio Science 2012,27(5):886-891.(in Chinese)
[6] ZOLTOWSKI M D,WONG K T.Closed-form eigenstructure-based direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid[J].IEEE Transactions on Signal Processing,2000,48(8):2205-2210.
[7] ZOLTOWSKI M D,WONG K T.ESPRIT-based 2-D direction finding with a sparse uniform array of electromagnetic vector sensors[J].IEEE Transactions on Signal Processing,2000,48(8):2195-2204.
[8] HE Jin,LIU Zhang.Computationally efficient 2-D direction finding and polarization estimation with arbitrarily spaced electromagnetic vector sensors at unknown locations using the propagator method[J].Digital Signal Processing,2009,19(3):491-503.
[9] RAHAMIM D,TABRIKIAN J,SHAVIT R.Source localization using vector sensor array in a multipath environment[J].IEEE Transactions on Signal Processing,2004,52(11):3096-3103.
[10] HE Jin,JIANG Shengli,WANG Juting,et al.Polarization difference smoothing for direction finding of coherent signals[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):469-480.
[11] GU Chen,HE Jin,ZHU Xiaohua,et al.Efficient 2-D DOA estimation of coherent signals in spatially correlated noise using electromagnetic vector sensors[J].Multidimensional Systems and Signal Processing,2010,21(3):239-254.
[12] LIU Zhaoting,HE Jing,LIU Zhong.Computationally efficient DOA and polarization estimation of coherent sources with linear electromagnetic vector-sensor array[J].EURASIP Journal on Advances in Signal Processing,2011.
[13] LUO Feng,YUAN Xin.Enhanced“vector-cross-product” direction-finding using a constrained sparse triangular-array[J].EURASIP Journal on Advances in Signal Processing,2012.
[14] WONG K T,YUAN X.Vector cross-product direction-finding with an electromagnetic vector-Sensor of six orthogonally oriented but spatially noncollocating dipoles/loops[J].IEEE Transactions on Signal Processing,2011,59(1):160-171.
[15] YUAN Xin.Coherent source direction-finding using a sparsely-distributed acoustic vector-sensor array[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(3):2710-2715.

