地-电离层中水平激发极低频场的勒让德展开算法

彭怀云 潘威炎 郭立新

(1.西安电子科技大学理学院，陕西 西安 710071；2.中国电波传播研究所，山东 青岛 266071)

引 言

水平激发的极低频(Extremely Low Frequency，ELF)(30 Hz以下)电磁波，主要应用于深潜通信和深部地质勘探.人工发射源均远远小于波长，可作为水平电偶极子源考虑.场强计算主要基于J. R. Wait[1]和J. Galejs[2]提出的地-电离层波导理论，场可表示为不同模阶数的勒让德函数及其一阶导数、二阶导数的级数和.其中，勒让德函数的复阶数ν由电磁波频率、地-电离层高度等参数确定.

当勒让德函数复阶数ν≫1时，勒让德函数及其一阶导数、二阶导数存在渐近表达式，地-电离层中水平偶极子激发的场存在近似解析解[2].Bannister据此提出了包含长大圆距和短大圆距两条传播路径的低频场强计算公式[3]，其计算结果的正确性已被超低频频段的大量试验所证实[4].

当勒让德函数复阶数不满足ν≫1条件时，勒让德函数及其一阶导数、二阶导数近似渐近表达式误差随频率降低而增大，不能准确描述低频场.对此问题，1999年Donald E. Barrick提出了球谐级数算法[5].该方法采用球谐级数的加速收敛算法，可以计算不同频率的垂直偶极子在地-电离层空腔中激励的场，但频率越低收敛越慢，计算量越大.国内学者利用球谐级数算法和时域有限差分法对此问题也进行了分析研究[6-7]，但这些方法均为数值计算方法，收敛缓慢，表达式物理意义不明确.

针对上述问题，作者在文献[8]中提出了对于橫磁波(Transverse Magnetic Wave，TM波)模及勒让德一阶导数的数值积分算法，解决了ELF垂直偶极子在地-电离层中场的求解问题.本文将在已有工作基础上，同时考虑横电波(Transverse Electrical Wave，TE波)和TM波传播模式及勒让德二阶导数的展开方法，提出一种水平电偶极子激发的ELF电磁波在地-电离层空腔中场的求解方法，并分析了ν≪1时的传播特点.

1 理论分析

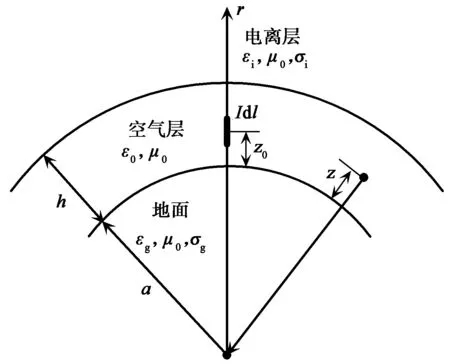
图1 地-电离层空腔模型

如图1所示的球坐标系，场源为位于θ=0，r=a+z0处的水平电偶极子，地面和电离层理想化为位于r=a和r=a+h处的两个均匀反射壁，其表面阻抗分别用Δg和Δi表示.场强观察点位于r=a+z处，取时谐因子为e-iωt，则在地-电离层空腔中传播的超低频(Super low frequency，SLF)及以下频段的电场可表示为文献[4]中式(10.3.14)，由此可知ELF的各个电磁场分量可理解为波导中各个传播波型的叠加，包含TM、TE波.在ELF频段，如果观察点远离发射源，发射与接收天线架设高度远小于波长及电离层高度，高度增益变化很小，则水平电偶极子产生的场的表达式为：

(1)

(2)

(3)

(4)

(5)

(6)

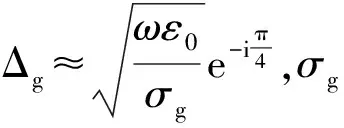
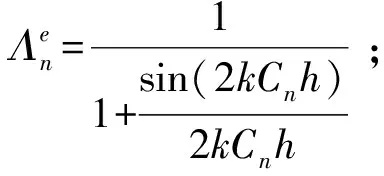
(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

为便于后续分析计算，若令

(15)

有:

(16)

2(z-1)cosθ·F(z-1，θ)+

(z-1)·F(z-2，θ)].

(17)

则式(1)～(6)可改写为：

(18)

(19)

(20)

(21)

(22)

(23)

因此，上述场强的计算重点为F(νn,θ)和F(μm,θ)等函数的计算.参考文献[2]所示的数值积分计算方法，F(ν,θ)的数值计算选取自适应Gauss-Kronrod积分方法[9]，其计算精度可达10-10.

2 计算分析与讨论

2.1 计算精度分析

1) 频率与TEM模复阶数关系

横电磁波(Transverse Electrical Magnetic Wave，TEM波)模为地-电离层空腔中可传播模，其它模均为速衰减模，因此，TEM模复阶数ν为ELF场强分布的关键影响因素，其实部和虚部随频率变化规律如图2所示.

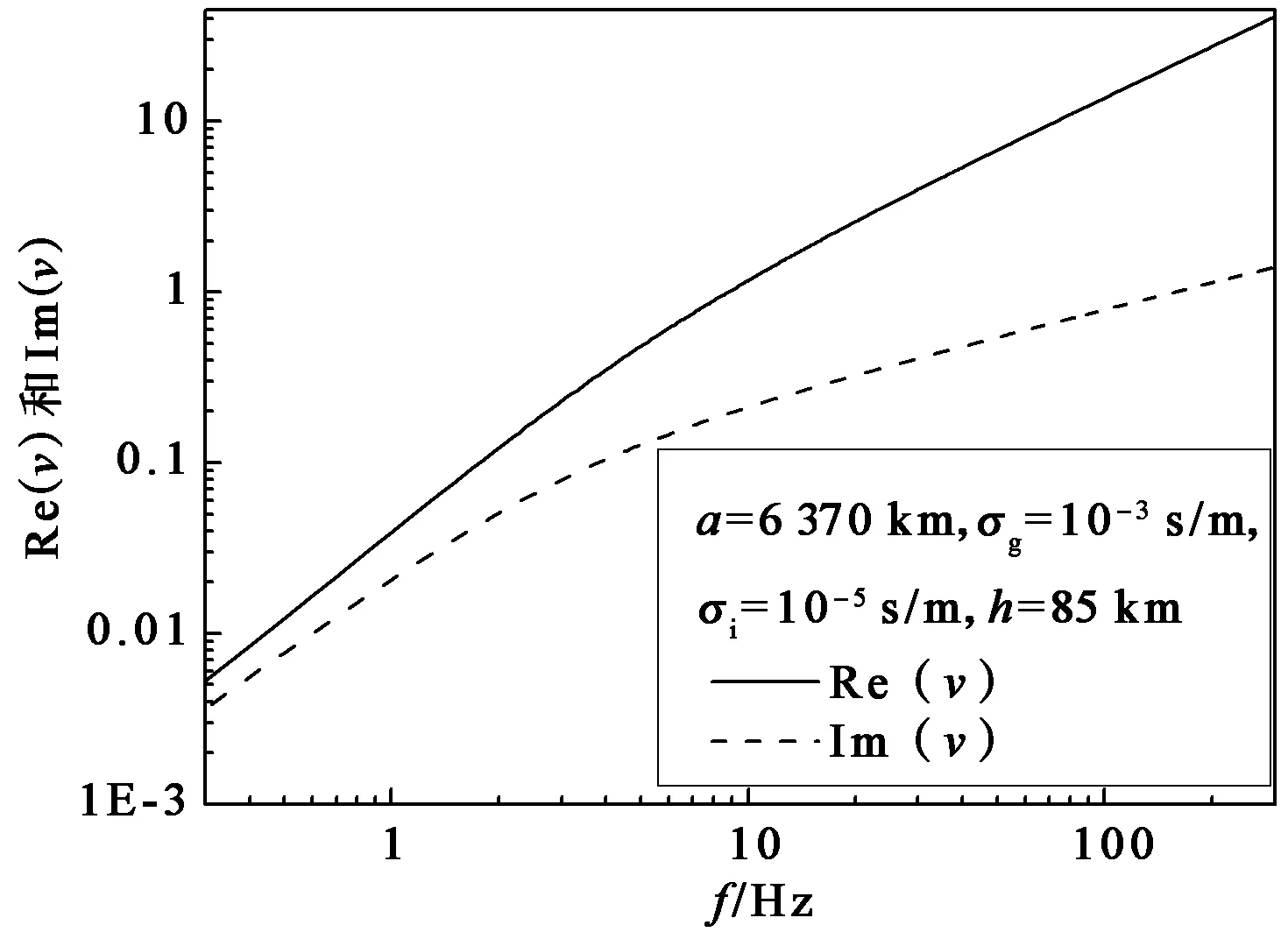
图2 ν的实部和虚部随频率的变化

由图2可见：在100 Hz以上ν的模为10以上，可认为ν≫1； 2 Hz以下ν的模为0.1以下，可认为ν≪1.

2) 近场精度验证

当观察点离发射源距离小于电离层等效高度时，为验证本文算法近场计算精度，将近场结果与半空间偶极子近场计算结果进行对比.由文献[2]知半空间偶极子电场、磁场水平分量计算公式为：

(kD)2]exp(ikD)；

(24)

(25)

(26)

(kD)2]exp(ikD) .

(27)

式中D=aθ.

在f=100 Hz，偶极子电流矩Idl=1，地面导电率为10-3S/m，电离层等效高度为85 km，发射、接收点均位于地面条件下时，本文算法计算至100阶模，半空间偶极子水平电场、磁场按式(24)～(27)计算，其结果对比如图3、4所示.

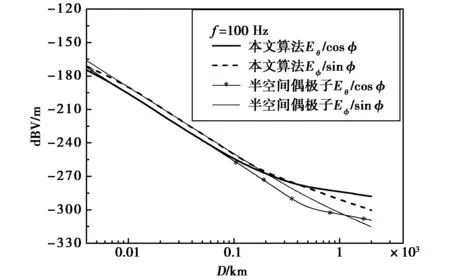
图3 水平电场计算对比

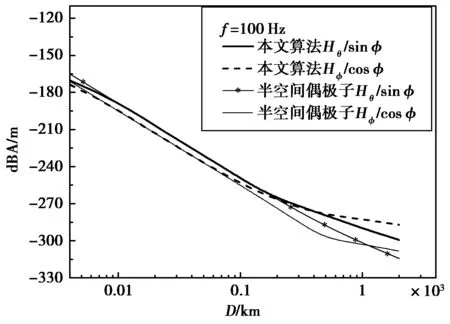
图4 水平磁场计算对比

从图3、4可以看出：在离开发射源10～70 km范围内，电离层影响较小，两种算法计算结果基本一致；离开发射源距离小于10 km时，由于本文算法仅计算至100阶模，导致结果与半空间偶极子辐射存在一定差异，理论上若本文算法计算至∞阶模，则两种算法将完全一致.

3) SLF频段远场精度验证

当ν≫1时，Bannister(dir.+ind.)公式的渐近表达式适用，为验证本文算法远场计算正确性，将本文算法与Bannister(dir.+ind.)公式计算结果对比.计算条件为：f=100 Hz，偶极子电流矩Idl=1，地面导电率为10-3S/m，电离层导电率为10-5S/m，电离层等效高度为85 km，发射、接收点均位于地面.计算结果如图5、图6所示.在对极点附近，由于Bannister(dir.+ind.)方法中勒让德函数渐进式存在奇点，其计算误差较大，导致两种算法在对极点附近存在差异.在15 000 km内，两种算法结果一致，由此验证了本文算法的远场计算精确性.

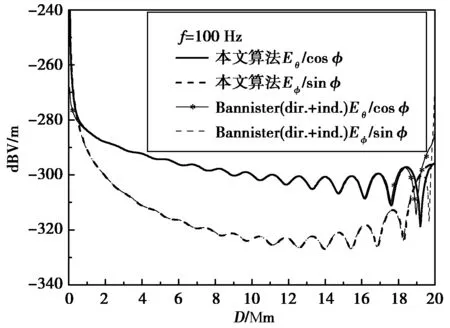
图5 远场水平电场对比

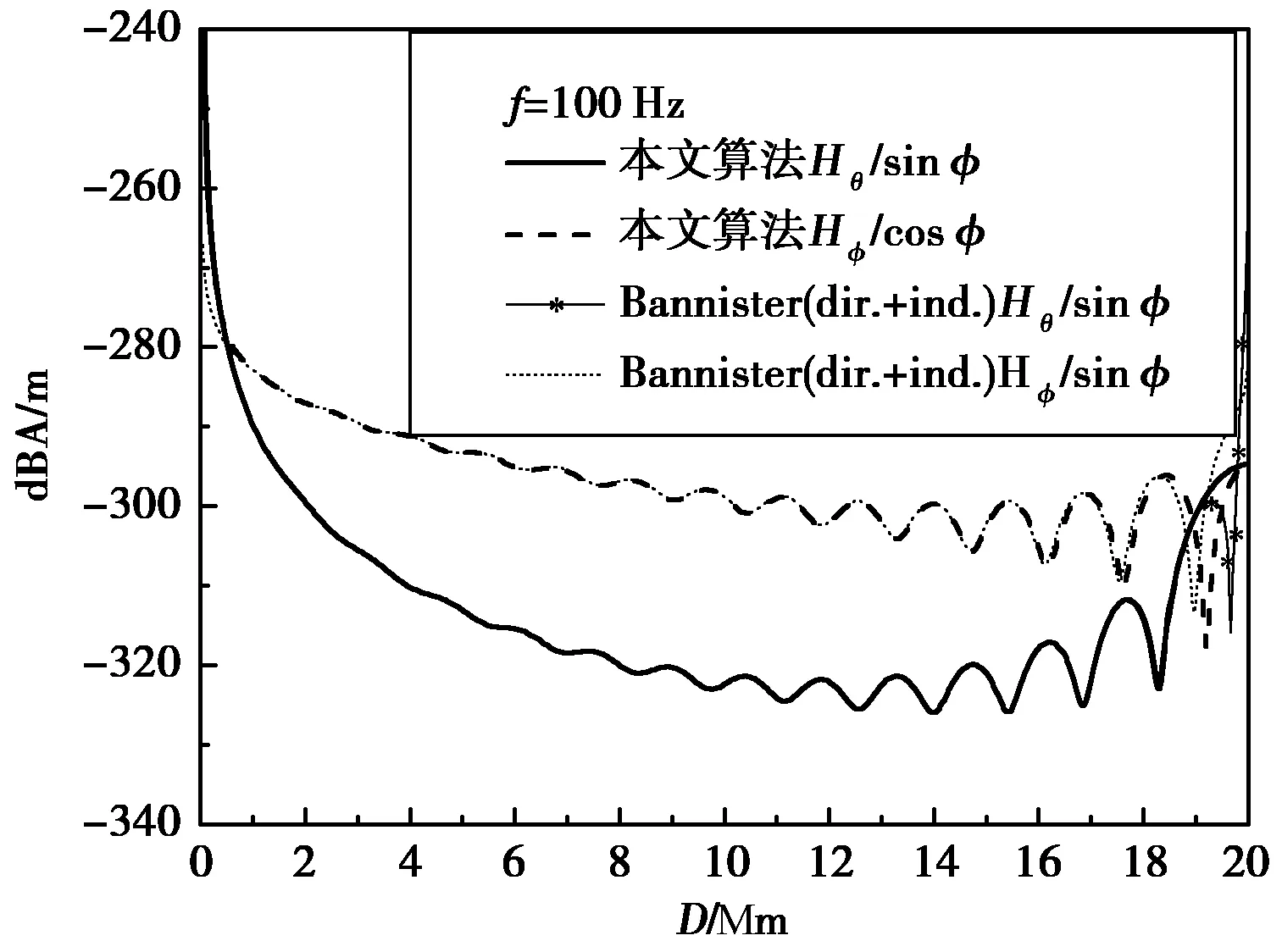
图6 远场水平磁场对比

2.2 SLF频段低端和ELF频段传播特性分析

在SLF频段低端和ELF频段，TEM模不满足ν≫1条件，Bannister(dir.+ind.)公式的渐近表达式逐渐不适用，如图7、8所示.其中偶极子电流矩为1 Am，地面导电率为10-3S/m，电离层导电率为10-5S/m，电离层等效高度为85 km，源点和观察点均位于地面(以下计算结果均采用基于上述计算参数).

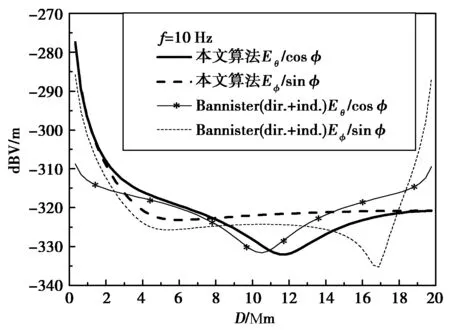
图7 10 Hz远场水平电场对比

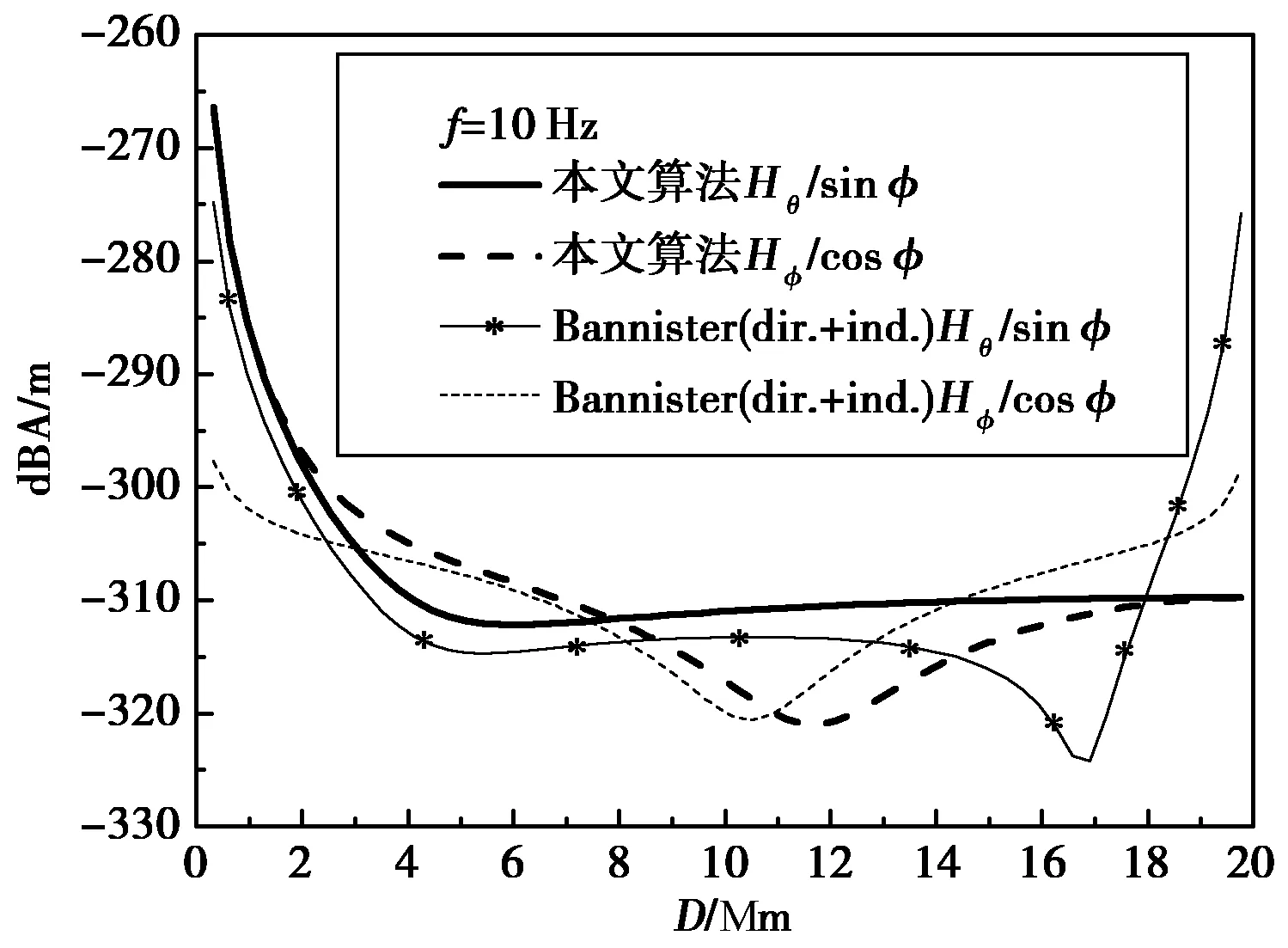
图8 10 Hz远场水平磁场对比

Bannisters公式中勒让德函数的渐近表达式误差很大，尤其在源点和对极点附近，而本文算法在对极点附近结果为一恒定值，符合物理规律，适合与ELF频段场强计算.

当ν≪1且ν→0时，即频率低于2 Hz时其水平分量随传播距离的变化如图9、10所示.两种算法差异更大.此时Bannister(dir.+ind.)公式的渐近表达式基本不适用.

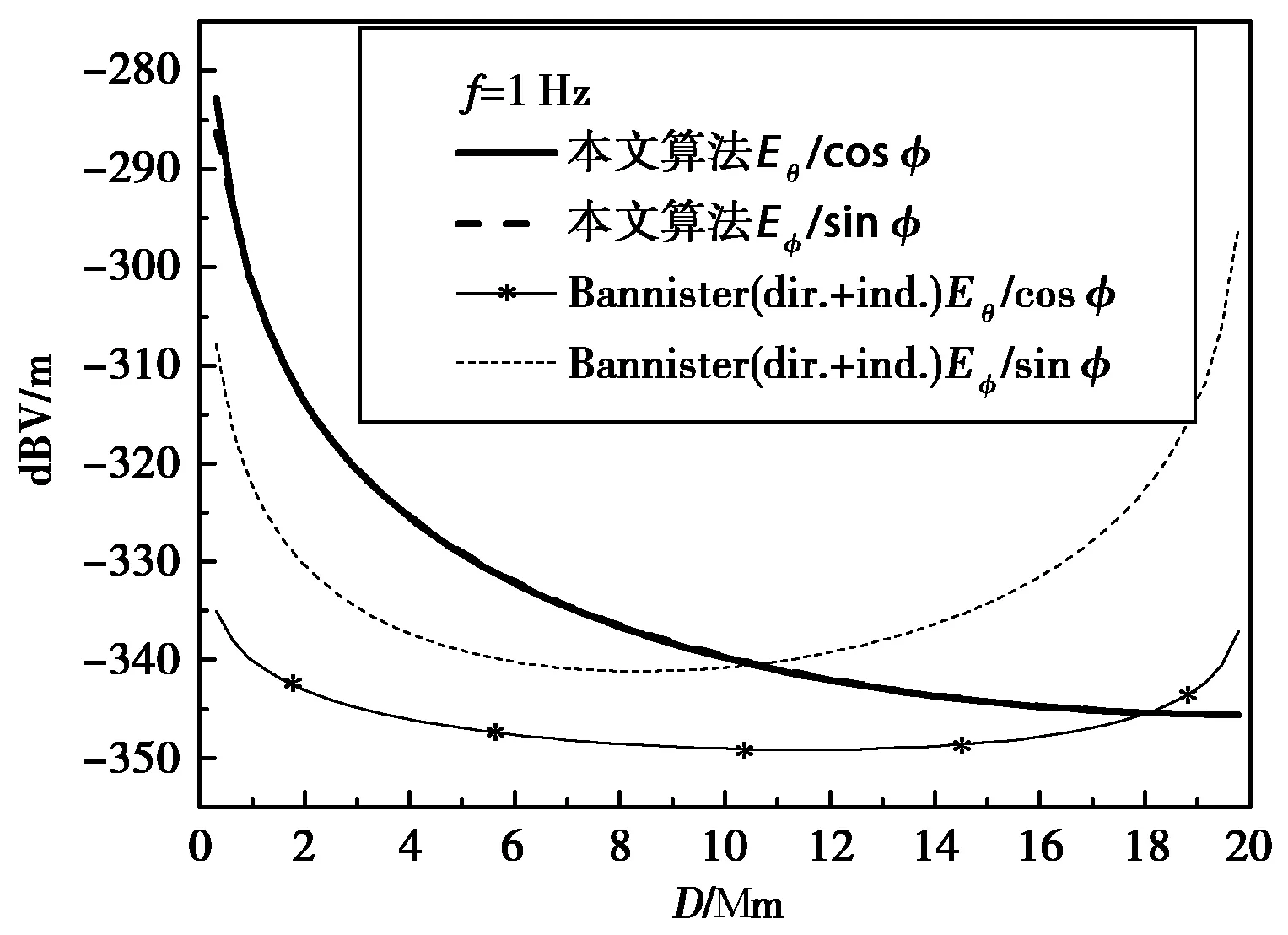
图9 1 Hz远场水平电场对比

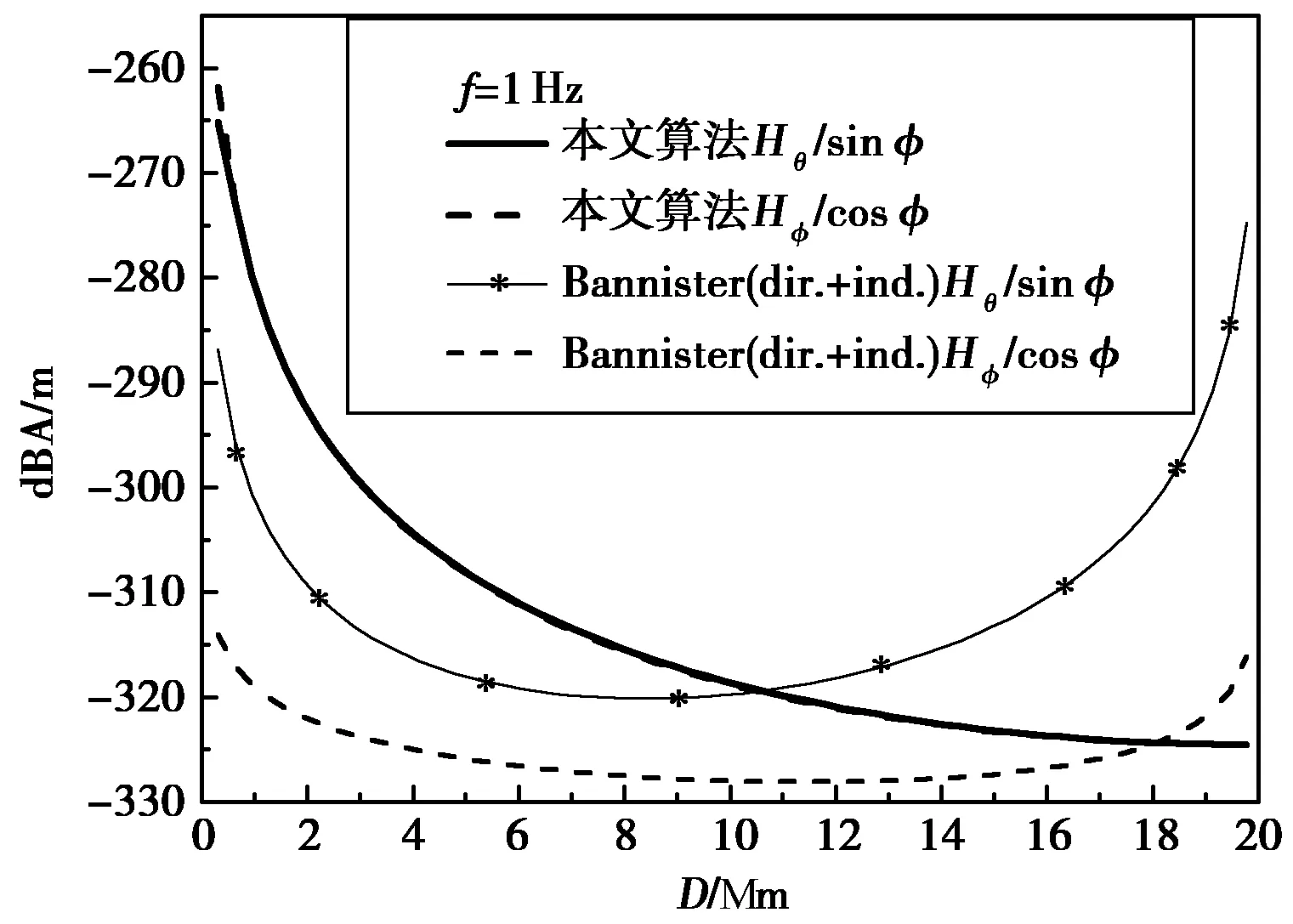
图10 1 Hz远场水平磁场对比

本文算法计算的水平分量场强随距离的等值线分布及其方向变化，如图11、12所示.

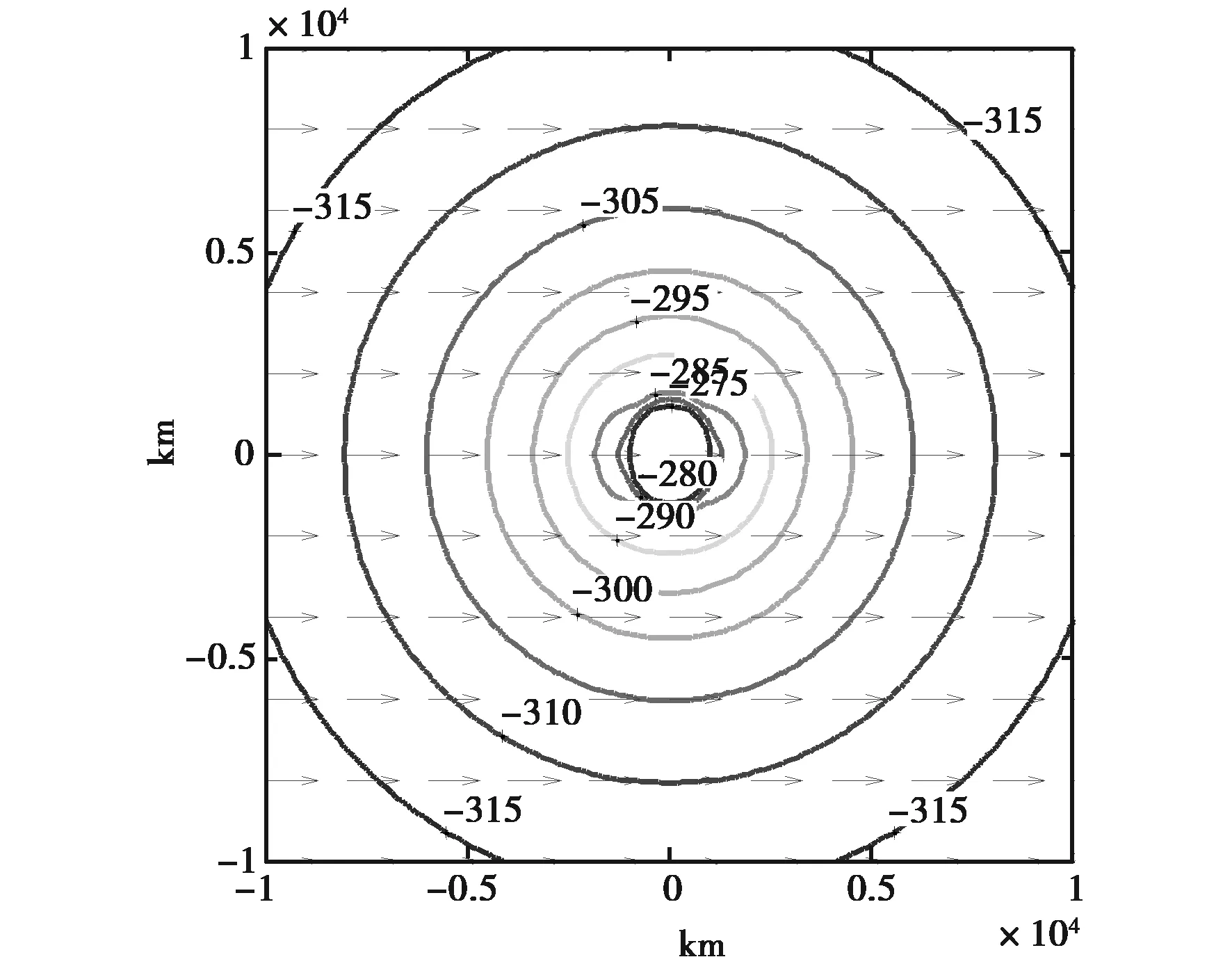
图11 f=1 Hz电场水平分量等值线及场方向图

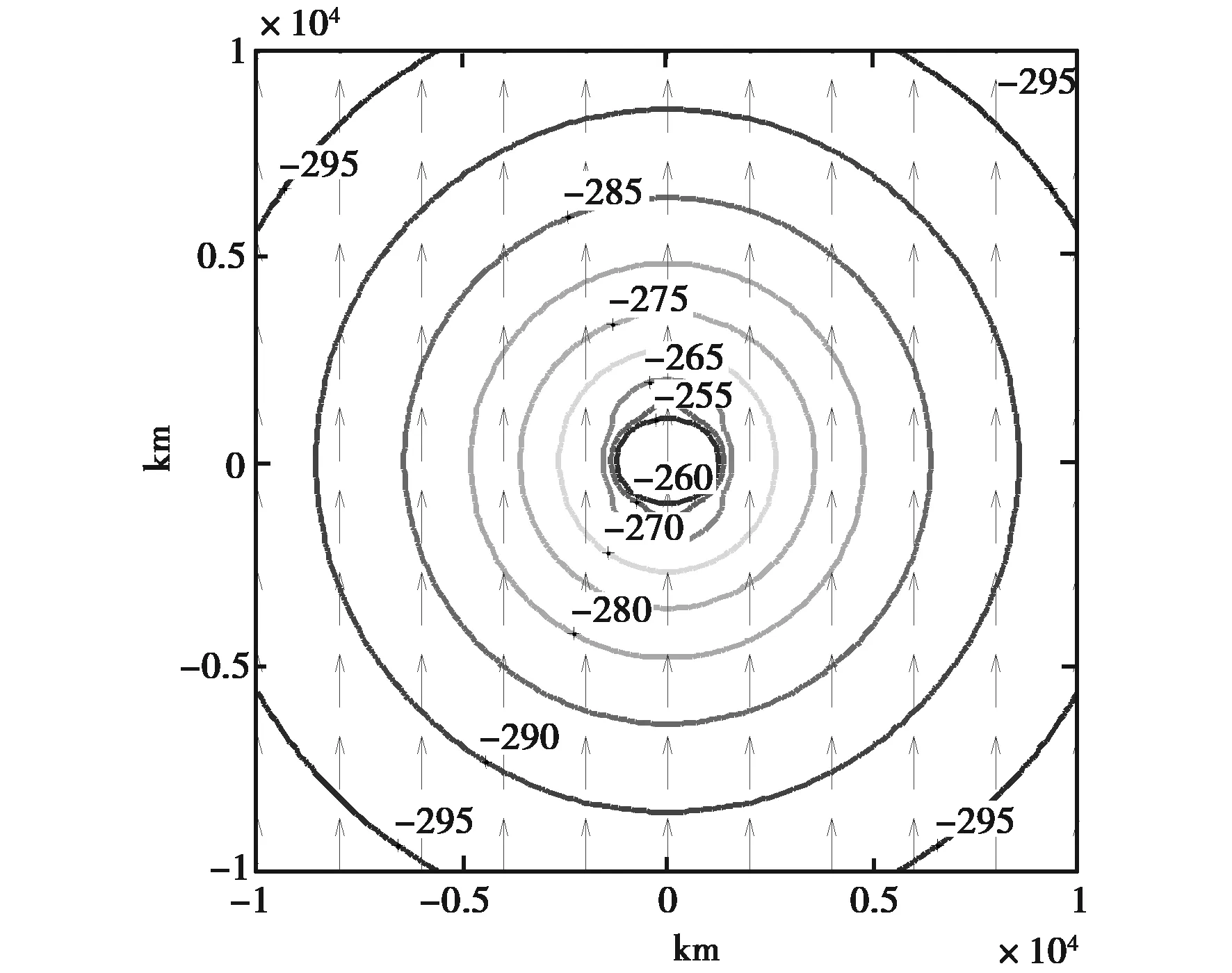
图12 f=1 Hz磁场水平分量等值线及场方向图

由图11、12可以看出：电场、磁场水平分量在2 000 km以后高阶速衰减模影响远远小于TEM模影响，场强等值线分布呈圆形，且在等值线分布图中水平电场方向平行于电偶极矩方向，磁场方向垂直于电偶极矩方向.另外，与图13所示100 Hz电场水平分量等值线图的等值线和方向图特性不同，表明在ν≪1时，ELF低频端(2 Hz以下)水平电场分布的特有规律.产生此种不同于高频分布规律的主要原因如下：

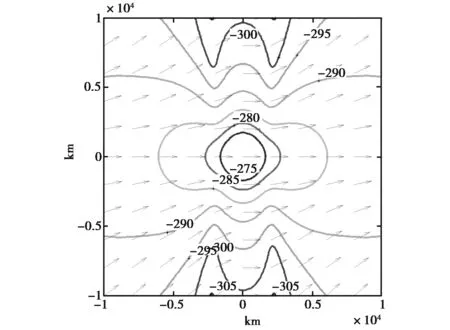
图13 f=100 Hz电场水平分量等值线及场方向图

据文献[10]中的式(8.762.1)

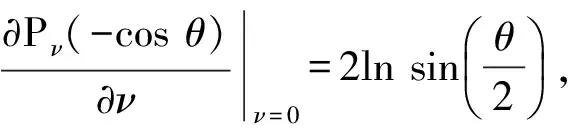
(28)

当ν→0时，Pν(-cosθ)可展开为

(29)

若取一阶近似，则当ν→0时，有

(30)

在频率较低时(2 Hz以下)，TEM模的ν→0，且其它高阶模在远区场强贡献可忽略，那么远区水平电场、磁场存在以下关系：

(31)

地-电离层腔体中远区电场、磁场的水平方向分量Et、Ht可表示为：

(32)

(33)

其幅度为

|Et|=|Eθ|,|Ht|=|Hφ| .

(34)

表明ELF低端远区场电场、磁场的切向分量仅随传播距离(或θ)变化，与方位角φ无关，与图9至12所示的ELF传播特性计算结果一致.

3 结 论

本文提出了一种地-电离层空腔中，水平偶极子激发的场强计算方法.该方法在近场、远场情况下所计算结果与半空间偶极模型、球形波导远区模型计算结果一致，印证了本文算法的正确性和精度.将本算法应用于几Hz以下的频点，计算结果可获得良好的数学解释，表明本文算法在近场、远场或更低频率计算方面，具有更好的适应性.

[1] WAIT J R. Electromagnetic Waves in Stratified Media[M]. Piscataway: IEEE Press, 1996.

[2] GALEJS J. Terrestrial Propagation of Long Electromagnetic Waves[M]. Oxford: Pergamon Press, 1972.

[3] BANNISTER P R. Simplified formulas for ELF propagation at shorter distances[J]. Radio Science, 1986, 21(3): 529-537.

[4] 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004: 333-368.

[5]BARRICK D E. Exact ULF/ELF Dipole field strengths in the earth-ionosphere cavity over the Schumann Resonance Region: idealized boundaries[J]. Radio Science, 1999, 34(1): 209-227.

[6] 王元新, 樊文生, 潘威炎, 等. 垂直电偶极子在地-电离层波导中场的球谐级数解[J]. 电波科学学报, 2007, 22(2): 204-211.

WANG Yuanxin, FAN Wensheng, PAN Weiyan, et al. Spherical harmonic series solution of fields excited by vertical electric dipole in earth-ionosphere cavity[J. 2007, 22(2): 204-211. (in Chinese)

[7] 董 慧, 闫玉波, 李清亮. FDTD模拟SLF/ELF水平电偶极子在非均匀地-电离层波导中的场[J]. 电波科学学报, 2010, 25(2): 276-280.

DONG Hui, YAN Yubo, LI Qingliang, FDTD analysis of fields excited by horizontal electric dipole in asymmetric earth-ionosphere cavity[J]. Chinese Journal of Radio Science, 2010, 25(2): 276-280. (in Chinese)

[8] 彭怀云, 陶 伟, 潘威炎, 等. 极低频垂直偶极子在地-电离层中场的数值积分算法[J]. 电波科学学报, 2012, 27(2): 333-338.

PENG Huaiyun, TAO Wei, PAN Weiyan, et al. Numerical integral method for elf fields excited by vertical electric dipole in asymmetric earth-ionosphere cavity[J]. Chinese Journal of Radio Science, 2012, 27(2): 333-338. (in Chinese)

[9] SHAMPINE L F. Vectorized adaptive quadrature in MATLAB[J]. Journal of Computational and Applied Mathematics, 2008, 211(2): 131-140.

[10] GRADSHTEYN I S, RYZHIK I M. Table of Integrals, Series, and Products[M]. New York: Academic Press, 1980.