量子比特在两个XY自旋环境中的纠缠动力学研究

张修兴，张国文

(渭南师范学院 a．物理与电气工程学院;b．人文与社会发展学院，陕西 渭南714000)

0 引言

量子纠缠是量子力学最令人着迷的特性之一，它是量子信息处理和量子计算过程中的重要资源［1-2］．近年来，不同封闭系统的热纠缠已经引起了人们研究的广泛关注［3-5］．但是，量子系统的纠缠度因为和周围环境的耦合作用，所以变得非常孱弱．这成为量子信息处理和量子计算的最大障碍．环境的退相干作用会导致系统纠缠度的降低［6］．因此，研究量子比特和环境耦合是纠缠演化量子信息科学的基本问题．

最近，量子比特和不同环境相互作用时的动力学问题引起了人们研究的兴趣［7-9］．特别是自旋环境中量子比特纠缠度随时间的演化问题成为研究的热点．目前，人们可以通过光晶格和冷原子技术实现不同的自旋环境［10-12］．因此，它成为研究粒子间各种关联作用与纠缠度关系的理想的平台．并且，自旋模型中存在量子相变现象［13］．而量子纠缠描述的是系统间的非经典关联，因此推测量子纠缠在系统相变点附近会表现出奇异行为．目前，很多学者对量子比特或者qutrits与自旋环境相互作用时的解纠缠过程［14-15］．Sun Z等［14］研究了Ising环境中量子比特的动力学行为，结果表明，在相变点附近，纠缠度按照时间的4次幂指数衰减;YuanZG等［15］研究了量子比特在相变点附近的解纠缠行为，发现量子相变现象会加速解纠缠过程．总结现存的这些研究结果，我们发现研究主要集中在量子比特与单个自旋环境相互作用．至于两量子比特分别和自旋环境相互作用时纠缠动力学行为还没有报道．

受上面研究的启发，我们研究量子比特和两个XY自旋环境相互作用时的纠缠动力学问题．结果表明，自旋环境的数目和对称性影响纠缠的动力学行为．通过调节两环境的参数，可以得到需要的纠缠演化速率．

1 模型和计算方法

模型如图1所示，量子比特1、2分别和环境e1、e2相互作用．每个量子比特可以用二能级原子代替［16］．并且假定量子比特只和自己的环境相互作用，环境之间没有相互作用．两环境的哈密顿量为

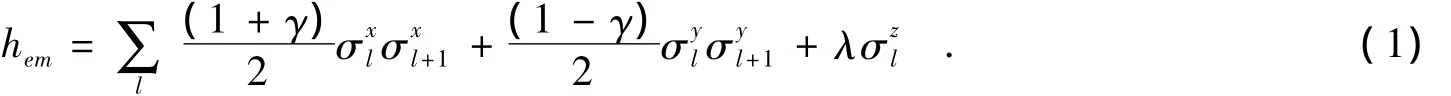
其中:m=1，2分别代表环境e1和e2，λ为外磁场的强度，σαl(α =x，y，z)为泡利矩阵，l表示的是自旋的位置，L为环境中包含的自旋总数，0≤γ≤1为各向异性因子．

从(1)式我们知道当γ=0时，hem对应的是各向同性XY模型;当γ=1时，hem变为Ising模型．

图1 量子比特1、2分别和自旋环境e1和e2相互作用示意图

量子比特和环境的相互作用为:

联立(1)(2)，可以得到量子比特和环境相互作用系统的总哈密顿量:

利用 Jordan-Wigner变换［13］

结合傅里叶变换［13］

那么，(3)式可以表达成

在(9)式中，通过 Bogoliubov变换［13］

系统总哈密顿量(3)最终可以写成完全对角化的形式:

其中:

并且定义a=2π/L．实际上，hem的对角化形式可以通过在(11)式中令耦合强度g=0来获得．

利用(11)式，我们可以得到系统总的时间演化算符:

接下来，我们从时间演化算符(15)出发，具体研究量子比特和自旋环境相互作用时纠缠度的演化．

2 结果和讨论

我们主要研究量子比特处于最大纠缠态时纠缠度的演化．假定量子比特的初态为:

其中:|0〉和|1〉分别表示自旋的向上和向下状态．自旋环境初始时处于真空态|φm〉=|0〉－k|0〉k，这里|0〉k满足dk|0〉k=0．那么，由量子比特和自旋环境组成的总系统的初始状态可以表示成Ψ(0)=|Φ〉，并且|ψ〉=|φ1〉|φ2〉．系统初态经过时间演化后，得到系统在t时刻的状态为:

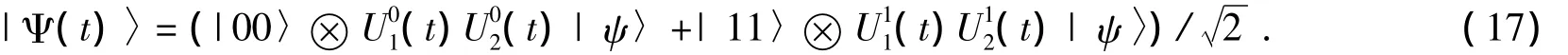
在(17)式中，把自旋环境的自由度消去后可以得到有关量子比特的约化密度矩阵为

从(18)式出发，利用Wootters提出的纠缠度量方案［17］，可以得到量子比特的纠缠度concurrence为

图2 量子比特和自旋环境存在弱耦合时，纠缠度随时间的演化

特别地，在式(20)中

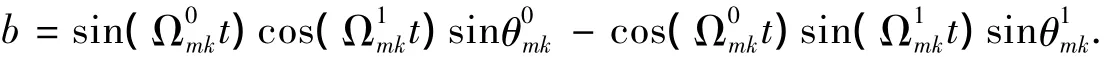
通过数值求解式(19)，我们可以得到量子比特纠缠度的演化．图2中，我们给出了三种情况下纠缠度随时间的变化，即两对称环境(DSE)、两环境不对称(DAE)和单个自旋环境(SE)条件下纠缠的演化．并且假定此时量子比特和环境间处于弱耦合状态(g＜λ)．这里需要说明的是:对称指的是两个自旋环境的参数相同，不对称指的是两个自旋环境的参数不相同．在DSE和SE中，我们假定L=300，γ=0．8，λ=2和g=0．3．对于 DAE，我们假定 γ1=0．8，γ2=0．9，g1=0．3，g2=0．4，其他参数和 DSE 以及SE 时相同．从图2中，可以看出纠缠度随时间振荡演化，但是包络线却是单调衰减的．特别地，在量子比特和两个环境(DE)相互作用时的衰减速度比量子比特和单个(SE)环境耦合时快．这是因为，量子比特和单个环境相互作用时环境会在两比特间诱发纠缠［18］．并且，还可以看出环境的对称会影响比特间解纠缠的速度，主要表现为在DAE中纠缠度包络线衰减速度比DSE中快．

图3 量子比特和自旋环境存在强耦合时，纠缠度随时间的演化

图3给出的是量子比特和环境强耦合时(g＞λ)，纠缠度随时间的变化．作图3的过程中，我们假设在DSE 和SE情况下，L=300，γ =0．8，λ =0．3，g=2．在DAE中，我们认为γ1=0．8，γ2=0．9，g1=2，g2=1，L1=L2=300和λ1=λ2=0．3．可以看出，纠缠度随时间单调衰减，但是不同环境衰减速度不同．在DE环境中，纠缠衰减的速率快于SE情况，这和图2的结果是一致的．但是，纠缠度在DSE衰减的速率比DAE的快得多，这个结果反映出纠缠对环境对称性的敏感性．通过比较图2和图3的结果，我们知道适当调节环境的参数，可以获得需要的解纠缠速率．

3 结语

研究了量子比特和两个XY自旋环境相互作用时的纠缠动力学问题．结果表明:自旋环境的数目和环境的对称性影响量子比特纠缠度的动力学行为．通过适当调节两环境的参数，可以得到需要的解纠缠速率．

［1］Einstein A，Podolsky B，Rosen N．Can Quantum-Mechanical Description of Physical Reality Be Considered Complete［J］．Phys．Rev，1935，47:777-780．

［2］Nielsen M A，Chuang IL．Quantum Computation and Quantum Information［M］．London:Cambridge University Press，2000．

［3］Wang X G．Entanglement in the quantum Heisenberg XY model［J］．Phys．Rev．A，2001，64:012313．

［4］Osenda O，Huang Z，Kais S．Tuning the entanglement for a one-dimensionalmagnetic system with anisotropic coupling and im-purities［J］．Phys．Rev．A，2003，67:062321．

［5］SkrØvseth SO．Entanglement properties of quantum spin chains［J］．Phys．Rev．A，2006，74:022327．

［6］Zurek WH．Decoherence，einselection，and the quantum origins of the classical［J］．Rev．Mod．Phys，2003，75:715-775．

［7］Lucamarini M，Paganelli S，Mancini S．Two-qubit entanglement dynamics in a symmetry-broken environment［J］．Phys．Rev．A，2004，69:062308．

［8］Cucchietti FM，Paz JP，Zurek WH．Decoherence from spin environments［J］．Phys．Rev．A，2005，72:052113．

［9］Cucchietti FM．Universal decoherence induced by an environmental quantum phase transition［J］．Phys．Rev．A，2007，75:032337．

［10］Rossini D，Calarco T．Decoherence induced by interacting quantum spin baths［J］．Phys．Rev．A，2007，75:032333．

［11］Cai JM，Zhou ZW，Guo G C．Stability of pairwise entanglement in a decoherent environment［J］．Phys．Rev．A，2005，72:022312．

［12］Duan LM，Demler E，Lukin M D．Controlling Spin Exchange Interactions of Ultracold Atoms in Optical Lattices［J］．Phys．Rev．Lett，2003，91:090402．

［13］Sachdev S．Quantum Phase Transition［M］．London:Cambridge University Press，1999．

［14］Sun Z，Wang X G，Sun C P．Disentanglement in a quantum-critical environment［J］．Phys．Rev．A，2007，75:062312．

［15］Yuan ZG，Zhang P，LiSS．Disentanglementof two qubits coupled to an XY spin chain:Role of quantum phase transition［J］．Phys．Rev．A，2007，76:042118．

［16］Quan H T，Song Z，Liu X F，et al．Decay of Loschmidt Echo Enhanced by Quantum Criticality［J］．Phys．Rev．Lett，2006，96:140604．

［17］Wootters WK．Entanglement of Formation of an Arbitrary State of Two Qubits［J］．Phys．Rev．Lett，1998，80:2245-2248．

［18］Braun D．Creation of Entanglement by Interaction with a Common Heat Bath［J］．Phys．Rev．Lett，2002，89:277901．