运用伸缩变换求解两个数学问题

安徽省旌德中学 赵忠华 （邮编：242600）

近期，《数学通报》问题解答栏目刊登了两道涉及椭圆点共线问题，给出的答案均比较烦琐，本文将用伸缩变换的方法给出比较简单的证明.首先介绍一下伸缩变换的有关内容.

并且我们有以下结论［1］：

1.任何不同的两点，只改变距离，不改变相对位置；

2.点分有向线段所成的比不变，特别是线段的中点依旧变为线段的中点；

3.两条平行线仍旧平行，两条相交直线仍旧相交，但交角改变；

4.点与曲线的相对位置关系不变；

5.直线与曲线相交、相切、相离的相对位置关系不变.

以下我们着手解决这两个问题：

数 学 问 题 2077［2］椭 圆b2x2＋a2y2＝a2b2（a＞b＞0）的外切 △ABC中，BC、CA、AB上的切点为D、E、F，过A作两直线分别与OB、OC交于M、N，且k·k＝k·k＝－，则AMOBANOC MN落在△ABC中位线的位置上.如图1：

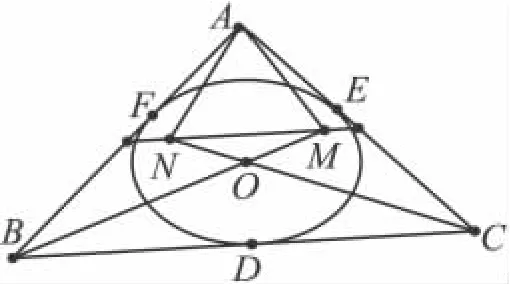
图1

我们只要在图2中证明问题结论成立即可，而这很容易证明.

不妨设

A（xA，yA）、B（xB，yB）、M（xM，yM）、O（0，0）， 变 换 后A′（xA′、yA′），B′（xB′、yB′）、M′（xM′，yM′）、O′（0，0），则

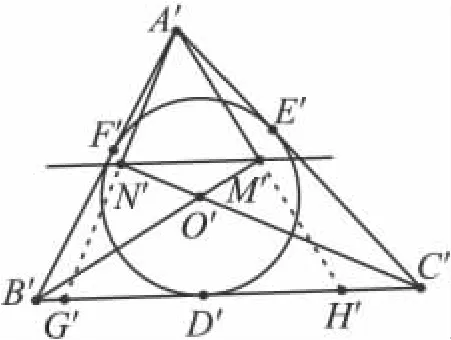
图2

所以kA′M′·kO′B′＝－1.

同理kA′N′·kO′C′＝－1.

因为kA′M′·kO′B′＝－1.所以A′M′⊥O′B′，所以 △A′M′B′≅ △H′M′B′，则点M′是A′H′的中点，同理点N′是A′G′的中点，M′N′／／B′C′，且M′N′落在 △A′B′C′中位线的位置上，于是MN落在△ABC中位线的位置上，命题得证.

图3

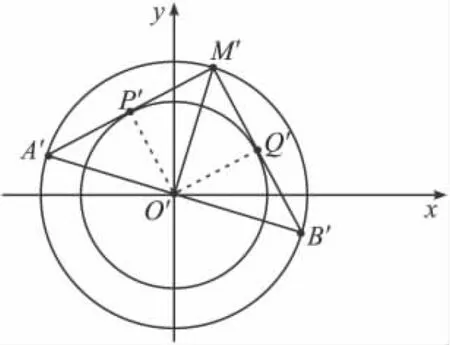
图4

从这两个问题的证明可以看出，对于椭圆中有关共线点、共点线或比例问题，通过伸缩变换将椭圆问题转换为圆中共线点、共点线或比例问题，可以轻松求解.

1 数学手册编写组.数学手册［M］.北京：人民教育出版社，1979

2 数学问题解答2077［J］.数学通报，2012，8

3 数学问题解答2092［J］.数学通报，2012，12