探索四面体的余弦定理案例及思考
浙江省温州市温州中学 刘旭飞 (邮编:325014)
这是笔者在市优质课评比中的课题——平面与空间中的余弦定理,它是承接普通高中课程标准试验教科书选修2-2第二章2.1节《合情推理和演绎推理》后阅读与思考的内容.它主要将三角形与四面体类比,由三角形余弦定理类比猜想得到四面体的余弦定理,同时由证明三角形余弦定理的方法类比得到证明四面体的余弦定理的方法.为什么要这么证?又是如何想到这种证法的?笔者认为,关注探究式教学的自然性、合理性,引导学生数学思维的自然形成、发展和深化,是我们一线教师急需关注的.现将课堂教学过程整理如下,与大家交流.
1 引入
黑板上画一个三角形.
教师:大家请看,这是平面里的三角形,在空间里选择什么图形作为它的类比对象呢?
学生:四面体.
教师:直角三角形呢?(学生暂时无法说出)
教师:直角三角形由平面直角坐标系中的原点、x轴上一点、y轴上一点构成.(黑板演示)
学生:直角四面体(在某一个顶点处三条棱两两垂直的四面体,叫直角四面体),可以把直角四面体放在空间直角坐标系中.
教师:很好,把两个类比对象的共性理解得越清楚,类比的结论的可靠性就越好.
教师:不管是二维还是三维的几何图形都是由基本元素组成.下面我们看看这两个图形元素之间的对应.(引导学生完成下表)


2条直角边和一条斜边 3个“直角面”和1个“斜面”_3条边的长度a,b,c 4个面的面积SA,SB,SC,S D_________∠A=90° ∠BAC=∠BAD=∠CAD=90°
记S*为顶点*所对三角形的面积.
教师:从二维平面到三维空间的类比,通常可抓住几何要素的如下对应关系:线与面;边长与面积;面积与体积;角与二面角;……
2 直角三角形与直角四面体类比
2.1 类比直角三角形的射影定理,猜想直角四面体的射影定理
教师:在直角三角形ABC中,过A作BC的垂线交BC于D(如图1),类比这个过程,该在直角四面体中作什么?


学生:过A作平面BCD的垂线交平面BCD于O(如图2).
教师:很好,由图1可得:BA2=BD·BC,这是直角三角形的射影定理,类比到直角四面体有什么结论呢?
教师:这就是直角四面体的射影定理,根据三垂线定理和面积公式易证,留给同学们课后完成.
2.2 类比直角三角形的勾股定理,猜想直角四面体的勾股定理
教师:由图1有:AC2=CD·BC,与BA2=BD·BC相加可得:AC2+AB2=BC2,这就是直角三角形的勾股定理,能否类比到直角四面体呢?
教师:这就是直角四面体的勾股定理,怎么证明?
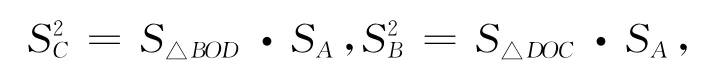
教师:非常好,这里不仅仅是内容层面的类比,更有方法层面上的类比.
3 三角形与四面体类比
教师:三角形的余弦定理是勾股定理的推广,直角四面体的勾股定理能否推广?能否类比三角形的余弦定理?
教师:类比三角形的余弦定理,试给出四面体余弦定理的猜想.

三角形的余弦定理:a2=b2+c2-2bccosA.
记(*,×)表示顶点*与×所对面在四面体内所成的角.
学生:


拖动点A、B、C、D改变四面体的形状,② 式仍然成立.
教师:类似2式的式子有几个?
学生:还有3个.(学生黑板演示)

教师:(2)式如何证明?(学生暂时无法说出)
教师:能否借鉴前面直角四面体勾股定理的证法?
一学生说:和前面一样,我们先证明三角形的余弦定理?
教师:很好,我们可以在平面中寻找灵感,然后类比到空间.那么如何证明三角形的余弦定理呢?(学生可能会利用向量来证明三角形的余弦定理,而且这种证明方法也是可以类比到空间中
教师:大家觉得这个结论正确吗?
学生:不对,应该是:

教师:为什么?
学生:可以用特殊情形检验,比如正四面体.
教师:嗯,这样做是比较明智的.类比的结论是否正确我们要先进行判断,然后进行调整,①式不正确,调整后的②式正确吗?(大概一半的学生回答正确)
利用《几何画板》验证,如图3,测量、计算数据如下:的余弦定理,但需要用到向量的外积,留给学生课后去找资料完成.)
教师:三角形中是否有类似直角三角形的射影定理?
教师:过A作BC的垂线交BC于点D,有什么结论?(如图4)
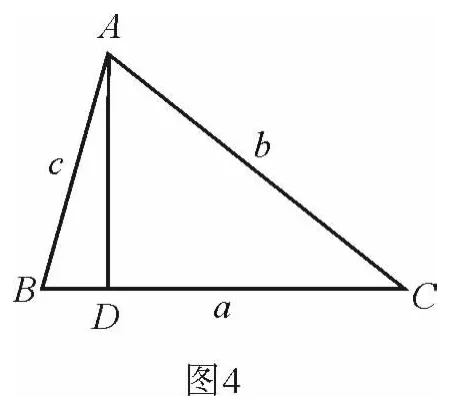
学生:a=ccosB+bcosC. ①
教师:很好,这就是三角形的射影定理,还有类似的式子吗?

教师:由三角形的射影定理能否证得三角形的余弦定理?
学生:将②,③代入①消去cosB、cosC,得a2=b2+c2-2bccosA.
教师:请大家考虑一下如何证明四面体的余弦定理?(学生分组讨论)


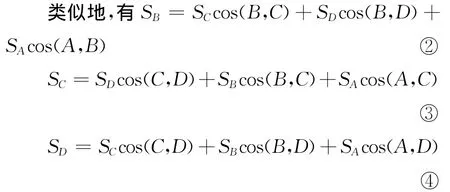
教师:不错,这就是四面体的射影定理.
学生:将 ②,③,④ 代入 ①,消去cos(A,D),cos(A,C),cos(A,B).即得

其他学生惊讶:太好了.
教师:很好,同学们我们回顾一下这节课的结构模式:

从中体会了类比方法的重要作用,类比不仅被用来发现问题,而且还能提供解决问题的思想和方法.事实上,这节课我们做了这么一件事情——将类比进行到底.
4 几点思考
(1)学生在做类比问题的时候,总觉得没有把握,好像是在猜谜,本质的问题是:学生对于可作类比的两个对象之间的共性或者相似性把握不够清楚,带有很大的随意性.所以教师应该引导学生关注类比对象元素是怎样对应的,有什么合理性,这样可以最大限度地帮助学生减少类比的盲目性.
(2)既要学会猜测,也要学会论证.在证明之前应该做适当的估计,可以借助于特殊化或者极端化的思想来检验.解决立体几何问题一般来讲常用的两种思路是:一是转化为平面几何问题;二是寻找一个平面几何相似的对象,通过类比获解.这说明类比在解决立体几何问题中的作用是不可忽视的,所以要引起高度的重视.
(3)通过直观地观察立体几何,学生无法精确认识其中的数学规律,利用几何画板测量出各对象的数量,然后通过拖动,在动态变化中进行观察,观察图形中的各种数量关系、探索图形中的不变量,有助于学生概括数学规律和进行理性思考,丰富了学生的感性经验.《几何画板》既有利于发挥学生的想象力、鼓励学生进行数学猜想,又可以迅速、准确地反馈和检验学生的猜想和直觉,加强学生的反思.

