基于蒙特卡洛法的卫星天线板展开精度分析

吴建云 王春洁 汪瀚

（北京航空航天大学机械工程及自动化学院，北京 100191）

（Mechanical Engineering and Automation School of Beihang University,Beijing 100191,China）

1 引言

合成孔径雷达（Synthetic Aperture Radar，SAR）卫星是自20 世纪70年代末发展起来的新型对地观察遥感卫星，其中有源相控平面阵型的SAR 卫星具有质量大、尺寸大、功耗大等特征，其在轨工作精度和天线机械精度紧密相关[1-2]。在空间展开状态下，大质量大尺寸的天线板主要是以悬臂状态装配于星体两侧，其工作精度受多重条件影响[3-4]，如卫星工作的热环境、结构加工装配误差、机体振动影响等，其中，由太阳辐射能和星体负载工作产生的热能可以通过隔热技术加以有效隔绝，振动的影响可以通过被动阻尼器和隔振设备加以隔绝，但结构加工和装配产生的误差不易消除。因此，分析加工装配误差对结构精度的影响对于整体卫星观察精度的性能评估具有重要意义。目前对机械系统的误差分析主要有经验公式法、极限误差分析法、确定性模型仿真分析法，但由于误差的不确定性和不精确性[5-8]，以上分析较为片面，所以可用概率的方法进行大量仿真，系统的评价误差带来的影响。本文利用蒙特卡洛法研究天线板机构中铰链锁定误差对精度的影响，根据铰链锁定误差统计分析结果定量地对天线板精度进行分析、评估和预测。

2 蒙特卡洛法理论

蒙特卡洛法又称统计模拟法，是一种以概率统计理论为指导，用概率模型来进行近似计算的方法。蒙特卡洛法的基础是大数定律和中心极限定理[9-10]。根据大数定律可知当抽取足够多的随机样本后，计算得到积分的蒙特卡洛值将收敛于该积分的正确结果。如要进行误差估计，则需要用到中心极限定理。该定理指出：无论单个随机变量的分布如何，许多独立随机变量之和总是满足正态分布，记为N（μ,σ2）。假设用g(x)来表示正态分布密度函数，其中μ为均值，σ为标准差，则

3 卫星天线板模型建立

3.1 动力学模型建立

天线拥有1 套可折叠的空间支撑桁架机构来保证其刚度和精度，根据展开支撑机构的设计原理，天线在轨展开之后由支撑机构固定在展开状态，而支撑机构的支撑结构则由具有位置锁定机构的铰链来实现。为保证展开状态的构型稳定和整体刚度，在展开状态为死点位置的铰链点，即两侧连杆呈180º的铰链点处，设置位置锁定机构来实现在指定位置的锁定。锁定铰链设置位置如图1 中红圈所示，其中A、O为机构与星体的连接点。支撑机构为3 维结构，假设平行于图1 构型中xy 平面且过天线板质心的平面为对称平面，则除铰链A、B、F 分布于整体机构的对称平面上之外，其余杆件和铰链均关于对称平面对称分布，共有9个锁定铰链，共同完成对支撑机构锁定位置的固定。本文利用Adams 软件进行动力学模型建立和仿真。

图1 天线板构型图Fig.1 Structure of the Antenna

当所有铰链锁定在理想位置、杆件保持绝对刚性的理想状态下，天线板保持理想平面度和指向方向。但在实际工况中，由于锁定铰链机构加工误差、装配误差的存在，导致铰链锁定结构在展开状态并不能锁定在指定角度上。由于结构在展开锁定之后为静不定结构，因此铰链的不精确锁定将会对结构整体产生内应力，从而使得天线板指向和平面度发生偏移，从而影响天线在轨工作的精度。

3.2 有限元模型建立

为了精确分析天线板由于铰链锁定误差导致的天线板精度变化，需要采用动力学模型结合静力学分析的方法对结构进行包含误差的力学分析。首先进行多柔体动力学仿真，将天线板从收拢姿态无内应力状态开始展开，直到铰链锁定，较为准确地模拟了误差在展开锁定过程中所发挥的作用，之后提取动力学模型中最后锁定时刻的结构关键节点受力，再使用有限元软件

进行静力学计算，可以得到精度较高的结构变形结果。为提高有限元计算效率，本文从整体有限元模型中分离出连接支撑机构与天线板的内外板框架结构，如图2所示，通过多柔体动力学模型仿真结果提取该子结构与整体结构其他部分连接点的内力，作为外力加载到该子结构上，可以简单快速地仿真在整体机构载荷下子结构的变形情况。

图2 有限元分析模型Fig.2 The finite element analysis model

3.3 精度指标

为了量化地衡量天线板发生变形的程度，引入2个主要的指标：平面度偏差和指向角度偏差。如图3所示。

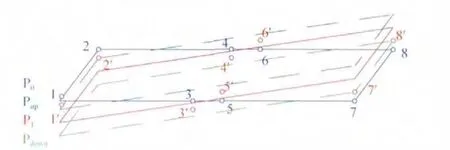
图3 平面度及指向角度偏差测量原理Fig.3 Measurement principle of flatness and pointing direction

在2个天线板框架上取8个点作为测量拟合点，每块天线板取4个点，分布于天线板框架与天线板连接处，测量其在引入误差情况下的坐标点位置，如式（3）所示，其中X,Y,Z 表示8个拟合点的x,y,z坐标组成的向量。

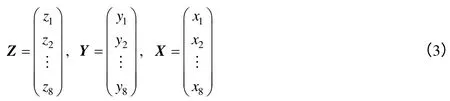
图3 中P0为2 块天线板名义标注平面，P1为由8个测量点通过回归算法拟合的平面。方程为

式中 x,y,z为拟合平面内任意点的坐标；β1,β2,β3为系数。

Pup为与P1平面相平行并通过距离P1平面上侧最远点的平面，同理Pdown为下侧距离P1平面最远的平面。

平面度偏差定义为Pup平面与Pdown平面的距离，记作d，表达式为

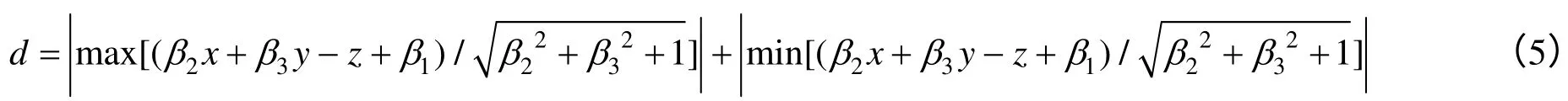
指向角度偏差θ 定义为P1平面与P0平面的夹角，表达式为

4 蒙特卡洛法模拟

由于在加工过程中锁定铰链的锁定误差为一个随机变量，并且每一个铰链误差值相互独立，且有较为详细的统计数据，因此本文选用蒙特卡洛法进行分析。

4.1 动力学模型建立

根据铰链安装位置的不同，展开支撑机构共使用了5 种9个锁定铰链。通过对实际使用的锁定铰链锁定角度的测量与统计，判断各铰链锁定角度均符合正态分布，得到该5 种铰链锁定角度的正态分布主要参数如表1所示，表中θB、θE、θH、θI、θO为图1 中B、E、H、I、O 处铰链锁定角度；θE_2、θH_2、θI_2、θO_2为图1 中E、H、I、O 处对称布置的铰链锁定角度。

表1 各锁定铰链锁定角度正态分布参数Tab.1 Normal distribution parameters of locking angle for each locking hinge

4.2 蒙特卡洛法分析流程

蒙特卡洛法的关键在于产生符合概率分布的高质量伪随机数和足够的采样点。本文使用多学科优化软件Isight 来实现蒙特卡洛法分析，集成多柔体动力学分析、有限元静力学分析以及Matlab 拟合计算等流程集成。蒙特卡洛法分析流程如图4所示。

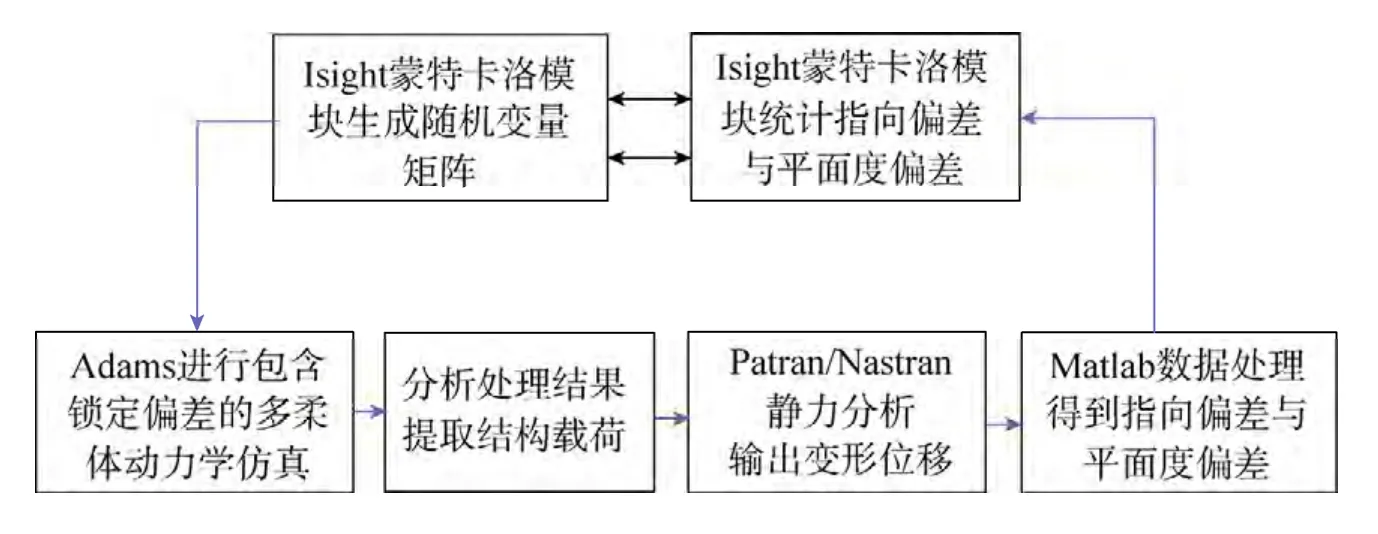
图4 蒙特卡洛法分析流程Fig.4 Analysis process of Monte Carlo method

5 仿真分析结果

5.1 蒙特卡洛样本分析结果

根据上述分布函数和流程，选取500个采样点进行蒙特卡洛法分析。每个采样点包含9个服从已知概率分布、相互独立的铰链锁定位置参数。统计分析结果得到平面度偏差的频数分布直方图如图5所示，指向角度偏差的频数分布直方图如图6所示。

图5 样本平面度偏差频数分布直方图Fig.5 Frequency distribution histogram of sample flatness error

图6 样本指向角度偏差频数分布直方图Fig.6 Frequency distribution histogram of sample pointing direction error

5.2 结果分布拟合与K-S 检验

根据蒙特卡洛法分析的结果可以得到指向角度偏差和平面度偏差的样本结果，为得到两者参数的整体分布情况并进行预测，可对分布直方图进行曲线拟合，从两者频数分布直方图中可以看出基本符合正态分布规律，先考虑使用正态分布进行拟合[11]。

通过对两者结果的统计分析，可得到样本中指向角度偏差和平面度偏差的均值和方差，同时可以给出估计的置信区间如表2所示。

表2 均值和方差整体估计的置信区间Tab.2 Confidence intervals for the estimated values of mean and variance

为检验正态分布拟合的可信度，采用K-S 检验（Kolmogorov-Smirnov）法来对拟合结果进行检验。

K-S 检验法是一种检验单一样本是否服从某预先假设的特定分布的方法，其做法是以样本数的累积频数分布与特定理论分布比较，若两者间的差距较小，则推论该样本取自某特定分布族。

假设目标分布为 F0(x)，样本采样分布为 F1(x)，，S (n,α )为样本容量为n、显著水平为α 时S 的拒绝临界值。

当 S ＞S (n,α)时，表示 F1(x)拒绝 F0(x)的假设，反之则接受 F0(x)的假设。

本文使用Matlab 软件中Kstest 函数算法对所得的指向度偏差与平面度偏差拟合的正态分布矩阵进行检验，取显著水平α=0.05，验证结果表明二者的采样结果均符合正态分布。

根据正态分布原则[12]，可对整体指向角度偏差和平面度偏差进行估计，即指向角度偏差下限(μ -3)σ为－0.076 4º，上限(μ +3)σ为0.495 4º，平面度偏差下限(μ -3)σ为2.0mm，上限(μ +3)σ为5.8mm，实际偏差落入以上区间的概率可达99.74%。

6 结束语

1）建立了卫星天线板动力学模型，可以提取天线板锁定铰链处受力，将力作用于建立的有限元模型，可进一步提取结构关键节点变形，作为蒙特卡洛法的分析基础。

2）给出了衡量天线板变形程度的2个主要指标即平面度偏差和指向角度偏差。

3）通过给出的铰链锁定误差分布进行蒙特卡洛分析，并将结果样本进行拟合、检验和预测，可得到平面度偏差和指向角度偏差均满足正态分布，两者的均值分别为3.9mm和0.209 5º，由此可进一步得到其置信区间以及满足3σ 原则[12]的变量上下限和概率。

通过蒙特卡洛分析得到的整体结果估计，对评估铰链锁定误差对结构精度的影响，以及实际结构中结构精度的偏差范围具有重要意义，并可为之后通过机械方法以及控制算法等途径减小误差影响，提高SAR 卫星分辨精度奠定基础。

References)

[1]孙永岩.合成孔径雷达卫星构型设计[J].航天返回与遥感,2008,29(3):45-50.SUN Yongyan.Synthetic Aperture Radar Satellite Configuration Design[J].Spacecraft Recovery &Remote Sensing,2008,29(3):45-50.(in Chinese)

[2]肖疆.合成孔径雷达天线技术的若干关键问题研究[D].北京：中国科学院研究生院,2006.XIAO Jiang.Study on Some Key Problems of Synthetic Aperture Radar Antenna Technologies[D].Beijing:Graduation University of Chinese Aeademy of Seiences,2006.(in Chinese)

[3]周成刚，李东旭.卫星大挠性桁架结构振动抑制试验研究[J].航天控制,2009,27(2):45-49.ZHOU Chenggang,LI Dongxu.Experiment of Vibration Suppression for Large Flexible Space Truss Structures of Satellite[J].Aerospace Control,2009,27(2):45-49.(in Chinese)

[4]张慧峰.空间可展开天线精度测量、热分析、可靠性分析及间隙影响研究[D].杭州：浙江大学,2010.ZHANG Huifeng.Surface Precision Measurement,Space Thermal,Reliability and Clearance Effect Analysis of Deployable Space Antennas[D].Hangzhou:Zhejiang University,2010.(in Chinese)

[5]丁希仑，周乐来，周军.机器人的空间位姿误差分析方法[J].北京航空航天大学学报,2009,35(2):241-245.DING Xilun,ZHOU Lelai,ZHOU Jun.Pose Error Analysis of Robot in Three Dmiension[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(2):241-245.(in Chinese)

[6]WU W D,Rao S S.Interval Approach for the Modeling of Tolerances and Clearances in Mechanism Analysis[J].Journal of Mechanical Design,2004,126(4):581-592.

[7]谢平,杜义浩,邢婷婷,等.机械系统误差分析新方法[J].计算机工程与应用,2011,47(7):36-39.XIE Ping,DU Yihao,XING Tingting,et al.New Error Analysis Method of Mechanical System[J].Computer Engineering and Applications,2011,47(7):36-39.(in Chinese)

[8]WU W D,RAO S S.Uncertainty Analysis and Allocation of Joint Tolerances in Robot Manipulators Based on Interval Analysis[J].Reliability Engineering and System Safety,2007,92(1):54-64.

[9]宋顺广.基于蒙特卡洛法的月球探测器着陆稳定性分析[OL].北京:北京航空航天大学学报,2012 [2013.4].http://www.cnki.net/kcms/detail/11.2625.V.20121129.1104.003.htm.SONG Shunguang.Landing Stability Analysis of The Lunar Lander Based on Monte Carlo Approach [OL].Beijing:Journal of Beijing University of Aeronautics and Astronautics,2012 [2013.4].http://www.cnki.net./kcms/detail/11.2625.V.20121129.1104.003.htm.(in Chinese)

[10]LU Y T,WANG C J,ZENG F M,et al.A Monte Carlo Analysis of Lunar Lander Dynamics at Touchdown [C]//CSAA.Proceedings of 2010 Asia-Pacific International Symposium on Aerospace Technology,Xi’an:Northwestern Polytechnical University Press,2010

[11]GB/T 4088-2008 数据的统计处理和解释：二项分布参数的估计与检验[S].北京：中国质检出版社,2008:40.GB/T 4088-2008 Data Statistical Process and Interpretation:Estimation and Inspection of Binomial Distribution Parameter[s].Beijing:China Quality and Inspection Press,2008:40.(in Chinese)

[12]李九龙，周凌柯.基于“3σ 法则”的显著误差检测[J].计算机与现代化,2012,1(3):10-13.LI Jiulong,ZHOU Lingke.Detecting and Identifying Gross Errors Based on“3σ Rule”[J].Computer and Modernization,2012,1(3):10-13.(in Chinese)