空间机械臂视觉相机内参标定技术研究

谭启蒙 胡成威 高升

（北京空间飞行器总体设计部，北京 100094）

1 引言

鉴于国际空间站的成功应用经验[1-2]，空间机械臂是深入开展航天活动不可或缺的重要组成部分，其作为支持空间站组装、运营、维护和空间应用的关键技术手段，承担着舱段转位、悬停飞行器捕获和辅助对接、舱外货物搬运、支持航天员出舱活动、支持舱外状态检查、支持舱外大型设备维修维护更换、照料暴露平台试验载荷、照料光学平台等任务。

空间机械臂在轨工作过程中，不仅自身需要实现大范围的运动转移，还特别需要完成一系列如设备拆装、货物抓取、舱段转位对接等高精度的精准操作[3]。为满足上述要求，空间机械臂的必备组成之一——视觉相机可以实现对机械臂整个工作区域的监控和观测目标的三维（3D）位姿测量，为机械臂在轨运行提供必需的图像信息和目标的位置、朝向以及运动信息。与目前各类航天器携带的载荷相机比较，机械臂视觉相机除兼顾以往传统的监视、观测功能外，还须具备检测识别观测目标、跟踪与测量空间位姿等功能。视觉相机测量原理主要是根据图像平面中的二维（2D）图像坐标及其所对应的3D 空间坐标之间的映射关系，解算出合作目标的空间位置姿态。为建立2D 图像坐标与3D 空间坐标之间的对应关系，就必须对视觉相机实施标定，以获取视觉相机内部成像模型中的所有未知参数[4]，即表征相机内部几何结构的内部参数，主要包括焦距、主点坐标、畸变系数等，并为空间目标位姿计算提供系数矩阵。因此，视觉相机内参标定作为空间机械臂至关重要的技术环节，是实现目标3D 位姿精确测量的基本前提和重要保障。

“加拿大臂”作为人类历史上第一个得到成功应用的空间机械臂，其自身携带的空间视觉系统SVS（Space Vision System）早在1990年就已成功完成了视觉相机的内参标定任务[5-6]。其标定原理是：利用相机在多个不同站位处，观测同一个位置已知固定的圆形标记点阵列图案靶标，根据前方交会原理，将所有图像代入摄影测量共线方程式，利用光束平差法解算出相机内方位参数值，从而完成内参标定。该标定方法标定精度高，但其不足之处在于：必须严格规定靶标的位置；在共线方程组求解与光束平差过程中，需要使用非线性优化算法，从而引入过多的非线性参数，这样不但不会提高标定精度，反而会引起解的不稳定性。针对这一问题，本文提出了一种基于2D 平面靶的空间机械臂相机内参标定方法，对靶标的位置不作特殊要求，即平面靶可在相机视场范围内随意运动；在内参求解中，实施分步计算，先利用线性成像模型计算焦距与主点初值，再引入畸变系数建立非线性成像模型，并利用非线性优化算法获取内参最优解，如此既能保证较高的标定精度，又能够确保最优解处于收敛状态，且有效简化了目标函数的计算难度。

2 空间机械臂视觉相机

2.1 视觉相机配置

视觉相机主要安装在机械臂的末端执行机构上，其采用单目测量方式，通常需要配置光源以增强、补偿相机对弱光照或恶劣光照条件的适应性，如图1所示。视觉相机的功能主要表现在以下几个方面：1）实时监控相机视场范围内的可操作区域；2）实时检测、识别与跟踪近距离处的空间合作目标；3）精确估计近距离处的空间合作目标的3D 空间位置姿态。

现以合作目标飞行器抓取捕获为例，简要概述视觉相机的工作流程：空间机械臂在轨执行任务过程中，当观测目标位于远距离处，机械臂按照预编程的路径规划，缓慢地靠近合作目标；当观测目标位于近距离处，目标已经成功进入视觉相机的有效视场范围内，视觉相机能够实时检测、识别与跟踪近距离处的空间合作目标，并精确估计近距离处的空间目标3D 位姿，从而引导机械臂末端执行机构进一步调整自身位置姿态以逐步减小其与空间合作目标之间的旋转差异和平移差异，确保机械臂末端执行机构能够准确捕获、抓取、锁定合作目标飞行器。

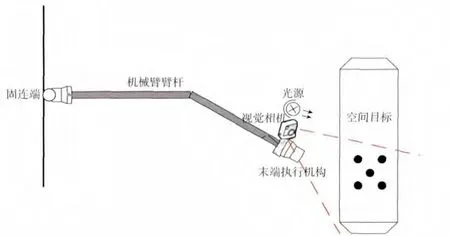
图1 空间机械臂视觉相机配置示意Fig.1 Configuration of space manipulator camera

2.2 视觉相机位姿测量原理

图2 解释了视觉相机位姿测量的基本原理。合作目标携带的某一个标记点P，该标记点P 与相机光心cO 的连线与像平面之间的交点q 即为该点在视觉相机成像面上所成的对应图像特征点。则3D 空间坐标值与2D 图像坐标值之间的函数关系可表示为[7]

式中 （u,v ）为点q 的2D 图像坐标，主要通过对采集图像信息进行亚像素图像特征点中心定位算法检测得到；（X0,Y0,Z0）为标记点P 在目标坐标系下的3D 空间坐标，通常利用电子经纬仪或激光跟踪仪等高精度测量仪器实施精密测量得到[8]，可视为已知量；A为视觉相机成像模型的内参矩阵，包括焦距、主点坐标、畸变系数等，主要依赖于视觉相机的内参标定结果；R,T 分别为旋转矩阵和平移矢量，为待求未知参数，形象描述了空间合作目标的包含6个自由度信息的相对空间位置姿态关系。

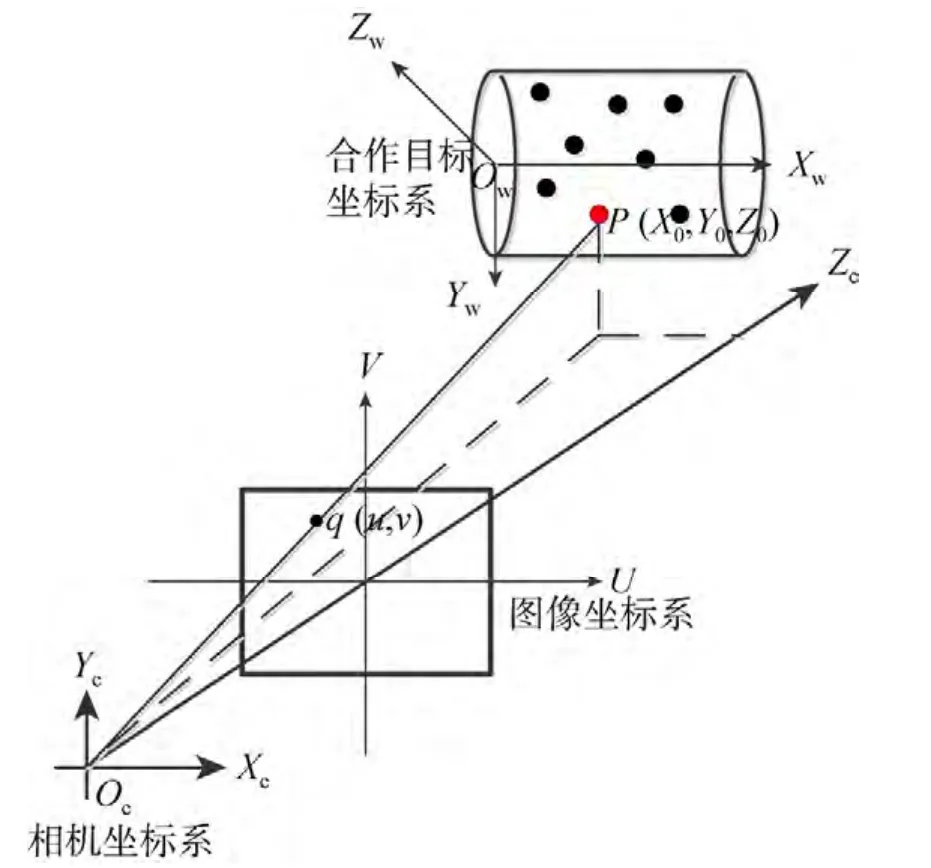
图2 视觉相机位姿测量原理示意Fig.2 Principle of estimation of position and orientation

3 视觉相机内参标定技术

空间机械臂视觉相机内参标定的目的在于准确计算焦距、主点坐标、畸变系数等相机内部固有参数，主要设计一种基于2D 平面靶的内参标定方法。与张正友标定方法相类似[9-10]，该法假定相机内部参数在整个标定过程中始终保持不变，即不论相机从任何角度拍摄标定靶，相机内参均为常数，只有外部参数发生改变。通过采集二维平面靶在不同方位下的多幅图像，利用平面靶和图像之间的点对应关系即可得到平面靶与图像平面之间的对应矩阵，即可得到相机内参的约束方程，利用非线性优化算法，从而解算出相机内部参数最优值。

基于2D 平面靶的视觉相机内参标定方法的数学计算过程具体如下。

假设平面标定靶上的某一个标记点M 的3D 空间坐标为(X,Y,Z)，其在相机图像平面上的对应特征点m 的2D 图像坐标为(u,v)，点m和M 的齐次坐标分别表示为(u,v,1)，(X,Y,Z,1)。根据视觉相机线性成像模型，3D 空间点M 与2D 图像点m 之间的映射关系为[7]

式中 (u0,0v)为主点坐标；α和β 分别为水平和垂直方向的等效焦距；γ为图像坐标轴的偏斜因子。

3.1 平面靶与相机图像之间的映射矩阵

不失一般性，以标定平面作为目标空间坐标系的xy 平面来建立目标坐标系，那么标定靶上特征点坐标满足：Z=0，记旋转矩阵R=[r1r2r3]，由式（2）得

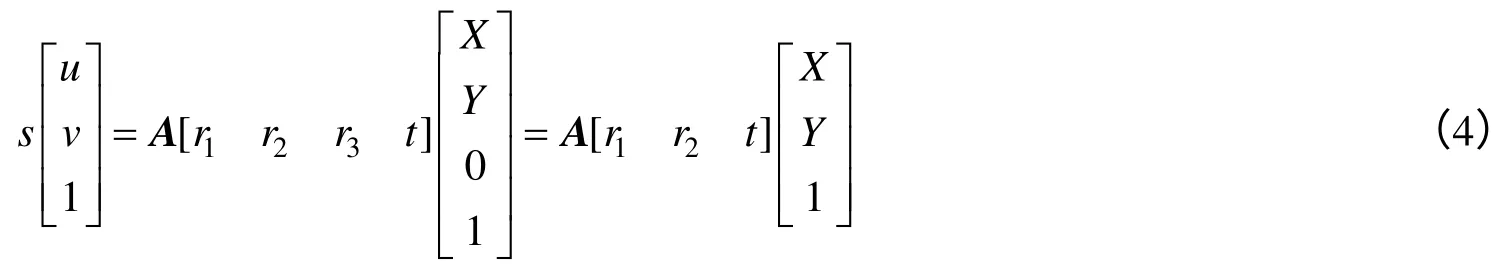
此时，用M=[X Y]T来代替M=[X Y Z ]T，记M～=[X Y1]T，平面标定靶上点M和对应像点m 之间可以通过映射矩阵H 来转换：

映射矩阵H 可以通过使得像点的重投影误差最小的优化方法来计算得到[9]，优化目标函数为

3.2 相机内参约束条件

设H=[h1h2h3]，从式（5）可以得出 [h1h2h3]=λA[r1r2t]，此处的λ 是比例系数，根据R的正交性[7]，可以得到为相机内参的两个基本约束条件：

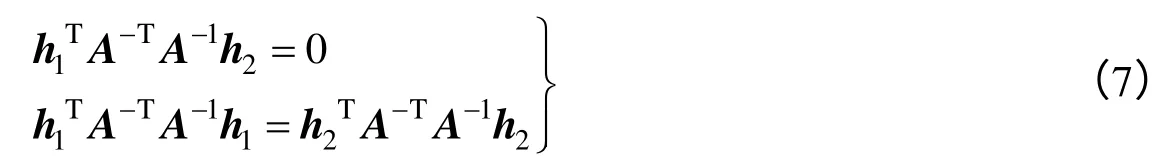
3.3 内参矩阵求解

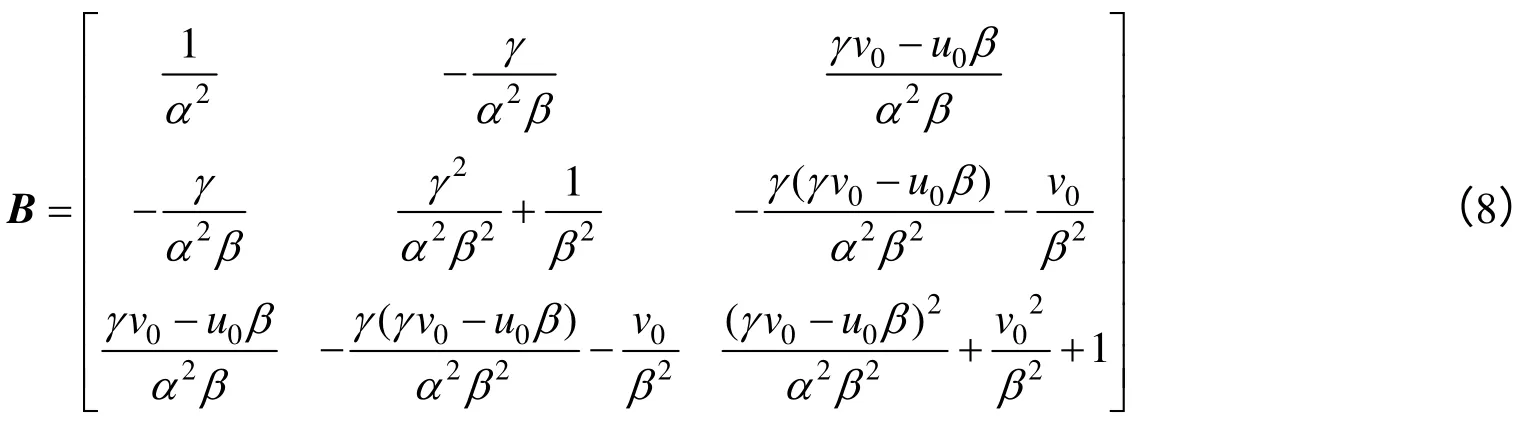
因为B 是对称矩阵，可以用六维的矢量b 来表示。

设矩阵H 的第i 列向量为hi=[hi1hi2hi3]T，则有

因此，可以将相机内参的两个基本约束关系式表示为

式（9）中，b为六维向量，因此，至少需要6个方程才能进行求解。移动平面标定靶至不同的位置，可以得到n（n≥3）幅图像，对应得到2n个方程，组合起来表示为

方程（12）的解对应于矩阵VTV最小特征值对应的特征向量。一旦b 求解出来，就可以通过Cholesky矩阵分解计算得到相机的内参矩阵A。

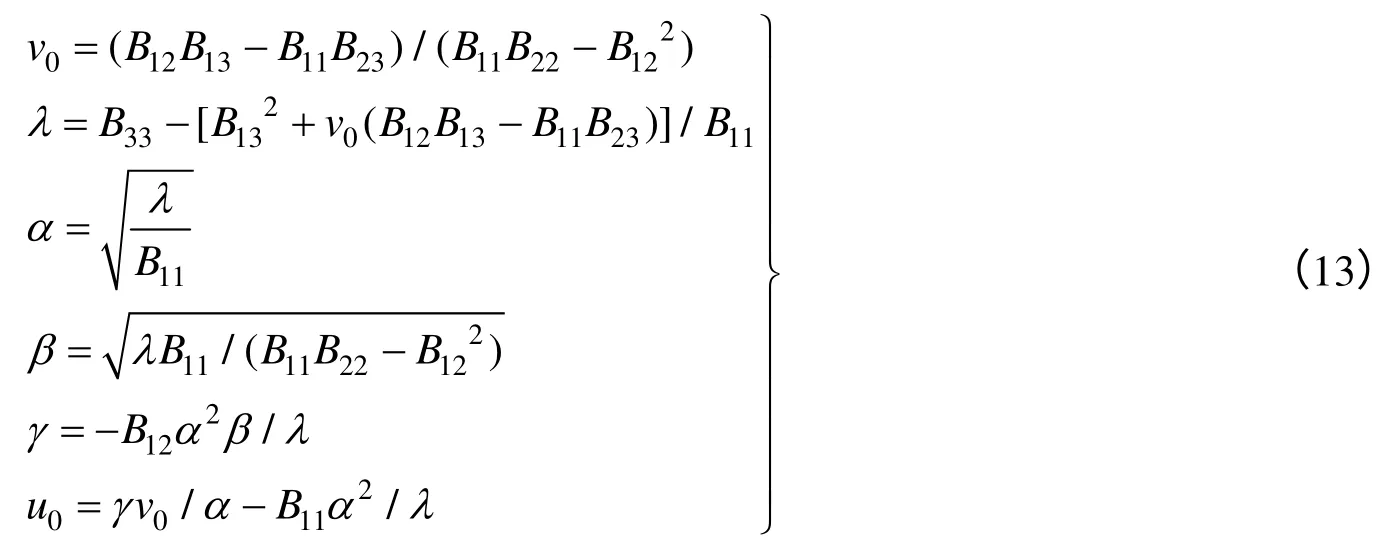
根据式（13）计算出的上述参数值对应了式（3）表示的内参矩阵A 的所有分量，这些参数即为相机标定的全部内参。

3.4 非线性模型

实际上，由于相机光学系统设计和加工误差而引起的图像几何变形较大，需要引入非线性的相机模型[10]。

相机的非线性畸变可以表示为

式中 （xu,yu）为由相机线性模型计算出来的图像点坐标；（xd,yd）为实际图像点的坐标；δx和 δy为非线性畸变值，它与图像点在图像中的位置有关，可表示为

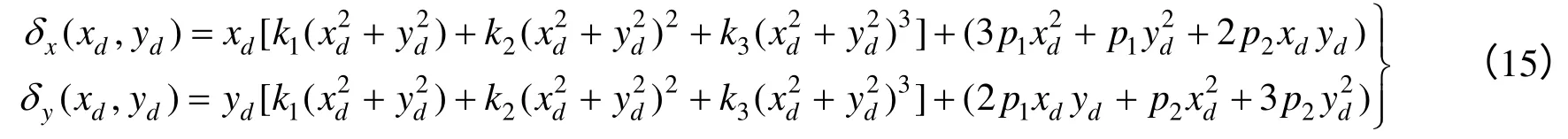
其中，δx和 δy的第一组多项式称为径向畸变，第二组多项式称为切向畸变。式（15）中，k1,k2,k3,p1,p2通常简称为（非线性）畸变系数。

最后，通过建立优化目标函数：

4 试验结果与分析

视觉相机内参标定试验旨在确定焦距、主点坐标、畸变系数等成像参数。现以空间机械臂视觉相机为例，完成相机内参标定试验。具体操作过程如下：

首先，将带有棋盘格图案的平面标定靶置于视觉相机的视场范围内；然后，利用相机先后拍摄平面靶在40个不同位置、姿态处的图像；随后，将所有采集后的标定靶图像分别代入上述基于2D 平面靶的标定算法中进行处理，根据靶面与图像平面之间的特征角点对应关系即可得到平面靶所在平面与相机图像平面之间的对应矩阵，以此建立若干相机内参的约束方程；最后，利用Levenberg-Marquardt 优化算法解算出相机内参矩阵最优解。

将上述40 幅不同位置处的平面靶图像分别代入内参标定算法进行计算，可得内参标定结果（如表1所示）。

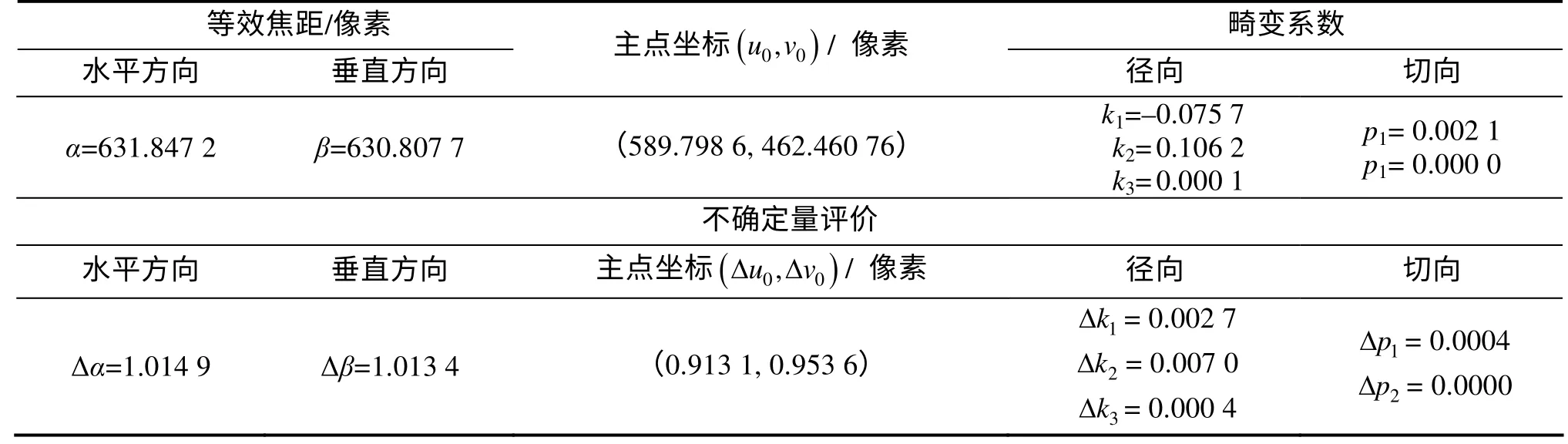
表1 视觉相机内参标定试验结果Table 1 Experimental result for calibration of camera intrinsic parameters

表1 列出了视觉相机内参矩阵A 中的焦距、主点坐标、畸变系数等不确定量，可视为相机内部参数的标定精度与误差水平。水平、垂直方向的归一化焦距的不确定量均近似于1mm，主点坐标不确定量不超过1个像素，畸变系数不确定量基本可忽略不计。鉴于上述分析可知，文中设计的一种基于2D 平面靶的内参标定方法可适用于机械臂相机内参标定，标定结果真实可靠，符合空间机械臂视觉相机获取合作目标3D 位姿的测量精度要求，可直接用于解算观测目标的位置、姿态。

5 结束语

为适应空间机械臂的实际任务需求，视觉相机不仅需要兼顾以往各类航天器携带的载荷相机的监视和观测功能，还必须具备观测目标检测识别、空间位姿跟踪与测量功能，也就是说，它能为机械臂在轨运行提供必需的图像信息和目标的位置、朝向以及运动信息。根据合作目标空间位姿测量基本原理，相机内参标定的目的是提供一组表征相机成像模型的可靠的内参矩阵，主要涉及焦距、主点坐标、畸变系数等，它是实现目标3D 位姿精确测量的重要保障。文中设计一种基于2D 平面靶的视觉相机内参标定方法有效解决了“加拿大臂”中视觉相机内参标定的计算复杂性等问题。该方法具有标定精度高、计算简便快捷等优点，主要表现为两个方面：1）该方法完全不受相机站位和靶标位置的限制，即平面靶可在相机视场范围内随意运动；2）求解内参约束方程时，实施分步计算，先利用特征值分解计算出相机线性成像模型中的焦距与主点坐标初值，再考虑引入径向畸变和切向畸变构建非线性模型，并利用Levenberg-Marquardt 非线性优化算法求解，可得到焦距、主点坐标、畸变系数等相机内参的最优解。空间机械臂视觉相机标定试验中，焦距标定误差近似于1mm，主点坐标误差不超过1个像素，所有畸变系数误差均忽略不计。因此，基于2D 平面靶的内参标定方法适用于机械臂相机内参标定，且标定结果均符合机械臂相机获取目标3D 位姿的精度要求，可直接用于解算观测目标的位置、姿态等后续任务。

References)

[1]于登云,孙京,马兴瑞.空间机械臂技术及发展建议[J].航天器工程,2007,16(4):1-8.YU Dengyun,SUN Jing,MA Xingrui.Suggestion on Development of Chinese Space Manipulator Technology[J].Spacecraft Engineering,2007,16(4):1-8.(in Chinese)

[2]秦文波,陈萌,张崇峰,等.空间站大型机构研究综述[J].上海航天,2010,(4):32-42.QIN Wenbo,CHEN Meng,ZHANG Chongfeng,et al.Surveys on Large-Scale Mechanism of Space Station[J].Aerospace Shanghai,2010,(4):32-42.(in Chinese)

[3]张凯锋,周晖,温庆平,等.空间站机械臂研究[J].空间科学学报,2010,30(6):612-619.ZHANG Kaifeng,ZHOU Hui,WEN Qingping,et al.Review of the Development of Robotic Manipulator for International Space Station[J].Chinese Journal of Space Science,2010,30(6):612-619.(in Chinese)

[4]http://www.asc-csa.gc.ca/eng/default.asp.

[5]http://www.asc-csa.gc.ca/eng/canadarm/vision.asp.

[6]G.MacLean S,Pinkey H F L.Calibration Procedures for the Space Vision System Experiment[J].Industrial Vision Metrology,1991,1526:113-122.

[7]张广军.视觉测量[M].北京:科学出版社,2008.ZHANG Guangjun.Vision Measurement[M].Beijing:Science Press,2008.(in Chinese)

[8]李广云.工业测量系统最新进展及应用[J].测绘工程,2001,10(2):36-40.LI Guangyun.The State of the Art and Applications of the Industrial Measuring Systems[J].Engineering of Surveying and Mapping,2001,10(2):36-40.(in Chinese)

[9]ZHAGN Zhengyou.A Flexible New Technique for Camera Calibration[J].IEEE Trans.on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.

[10]马颂德,张正友.计算机视觉——计算理论与算法基础[M].北京:科学出版社,2003.MA Songde,ZHANG Zhengyou.Computer Vision——Computational Theory and Algorithm[M].Beijing:Science Press,2003.(in Chinese)

[11]Marquardt D W.An Algorithm for Least-squares Estimation of Nonlinear Parameters[J].Journal of the Society for Industrial and Applied mathematics,1963,11(2):431-441.

[12]Madsen K,Nielsen H B,Tingleff O.Methods for Non-linear Least Squares Problems[M].Copenhagen:Informatics and Mathemetical Modelling Technical University of Denmark,2ndEdition,2004.

[13]Jose Pujol.The Solution of Non-linear Inverse Problems and The Levenberg-Marquardt Method[J].Geophysics,2007,72(4):W1-W16.