微振动对干涉仪运动机构均匀性的影响分析

段鹏飞 李明 徐彭梅

（北京空间机电研究所，北京 100094）

1 引言

基于干涉型的傅里叶变换光谱探测技术具有探测通量大、光谱波段多、光谱分辨率高等诸多优点，逐渐成为国内外光谱探测技术发展的热点[1-3]。光谱探测的目的是得到被测光束的光谱信息。光谱探测首先对被测光束进行时间或空间上的调制，获得被测光束的干涉信号；再对干涉信号进行傅里叶逆变换，得到被测光束的光谱信息，完成光谱探测任务。光谱探测过程中，通过干涉仪（本文指双角镜摆臂式干涉仪）得到干涉信号，干涉信号直接决定了光谱图品质，因此干涉仪技术是光谱探测的关键[4]。

为获得高品质的干涉信号，需要保证干涉仪自身回转机构的精密摆动，以实现干涉光程差的均匀扫描调制。而高精度的光谱探测对干涉仪光程差速度的均匀性提出了极高的要求。但是入轨后，卫星上飞轮、扫描机构、机械制冷机等设备的微振动会影响到干涉仪的速度均匀性。

一般来讲，干涉仪的速度均匀性主要是由机构控制系统来保证的，但实际工程中往往会遇到由于控制算法不成熟，控制系统对均匀性的保证不明确的情况。为了明确这种情况下微振动对干涉仪的影响，确定干涉仪能够承受的微振动临界值，本文提出了一种定量分析和评价的方法。

2 干涉仪光程差速度的均匀性

干涉仪运动机构的速度均匀性可以通过干涉光程差速度的稳定度来进行定量的判定。为满足高精度的光谱探测任务，干涉仪需要保证足够高的光程差速度稳定度，而这须通过运动机构的精密摆动来实现[5]。

2.1 干涉仪的光程差

双角镜摆臂式干涉仪通过摆臂带动两个角镜（cube corner）的摆动，实现光程差的扫描。干涉仪光路如图1所示。

图1 中，被测准直光束在分束镜上被分成反射光束A和透射光束B，A 光束经过角镜CC1 反射回来，并透射穿过分束镜，到达探测器；而B 光束经角镜CC2 反射回来后经分束镜反射也到达探测器。这样光束A、B 就在探测器上产生干涉图信号。定义A、B 光束光程相等的位置，即图中CC1和CC2所在位置为干涉仪的零光程差位置（zero path difference，ZPD）。

当摆臂绕着轴O 逆时针旋转角度为θ 时，角镜CC1、CC2分别移动到CC1´、CC2´位置。相对于ZPD 位置，A 光束多走了2个机械程差d，B 光束少走了2个机械程差d，故此时光束A和B 的光程差（optical path difference，OPD）为4d。易得d=R⋅sinθ，其中R为干涉仪摆臂回转半径长度。因此双角镜摆臂干涉仪的光程差D为[6-7]

图1 干涉仪光程差Fig.1 Interferometer optical path difference(OPD)

2.2 干涉光程差速度稳定度

由式（2）可看出，光程差速度取决于干涉仪摆臂回转半径R、摆臂的摆角 θ(t) 以及角速度。干涉仪光程差的均匀扫描调制要求光程差的速度v为匀速。

光程差速度的均匀性一般用光程差速度稳定度来定量描述。首先定义光程差速度的不稳定度α，α是干涉仪角镜在有效光程范围内所有光程差速度采样的标准差与均值的比值，一般要求α＜1%[8-9]；光程差速度的稳定度定义为（1–α），一般要求（1–α）>99%。

3 微振动影响的分析方法

本文的工作是为了确认当机构控制系统对摆臂速度均匀性保证不明确情况下，干涉仪能够承受的微振动临界值。由于控制系统的影响不明确，分析过程认为其对外部环境没有任何影响。同时假设，微振动下任意瞬态时刻干涉仪摆臂摆角是这一控制系统摆角与微振动引起摆角的线性叠加。然后利用这样的干涉仪摆臂摆角得出光程差速度均匀性的结果，进而定量判断微振动对一定机构控制系统下干涉仪可靠性的影响。

这种分析方法将微振动引起的干涉仪响应纳入到机构运动稳定性的分析中，能够确保可靠性分析结果更为真实。

3.1 基本假设

微振动激励直接影响干涉仪摆臂的摆角行程 θ（t ）和摆动角速度。假设微振动条件下，干涉仪摆臂摆角 θ（t ）是机构控制系统控制的摆角 θc（t ）和微振动引起摆角 θd（t）的线性叠加，即

需要说明的是，这里的机构控制系统的摆角 θc（t）不包含速度均匀性的保证。

则干涉仪摆臂摆动角速度为

此时干涉仪摆臂的光程差为

相应的光程差速度为

可以看到，微振动影响下光程差速度是4个变量的函数。

3.2 摆臂的运动特性

上述机构控制系统下，干涉仪摆臂摆动的角度 θc(t)和角速度可以通过光程差及其速度的定义推导得到。根据式（2）有

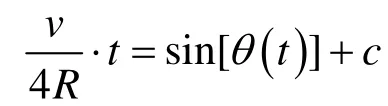
其中c 是常数。定义t=0 时，干涉仪摆臂位于光学零位（ZPD），此时干涉仪摆臂转角行程θ=0，故c=0。

因此机构控制系统下干涉仪摆臂摆动的角度 θc(t)为

而微振动引起的干涉仪摆臂摆动的角度响应 θd(t)和角速度响应，可以利用干涉仪结构的有限元模型，通过离散时域响应求解得到。

4 某干涉仪微振动影响分析

某干涉仪，如图2所示，通过安装耳与卫星平台连接。其搭载的平台装有飞轮，同时载有多台扫描机构和制冷机载荷，平台振动激励频率集中在90Hz、70Hz、50Hz 以及30Hz 处，微振动3个主轴方向同时激励在干涉仪安装耳板。为了明确平台扰动对干涉仪工作的影响，利用本文介绍的方法对上述激励下该干涉仪的速度均匀性进行分析。

图2 某干涉仪结构Fig.2 Model of the interferometer

该干涉仪有两种工作模式，相关的参数如表1所示。

表1 某干涉仪特征参数Tab.1 Parameters of the interferometer

首先求解一定机构控制系统下的摆臂角度及角速度。考虑到arcsin(x) 在区间为单调增函数，故摆臂回转的最大摆动角度，算得 θmax=0.036rad。

由式（7）、（8），可推导出机构控制系统决定的摆臂回转角 θc(t)和回转角速度（如表2所示）。

表2 摆臂控制系统下运动特征Tab.2 Movements of swinging arm in control system

然后利用干涉仪结构有限元模型（如图3），求解时域响应，得到微振动引起的摆臂角度及角速度的响应。根据平台扰振源的频率特性，微振动条件分别选取频率 90Hz、70Hz、50Hz、30Hz，加速度幅值50×10–3gn、30×10–3gn、10×10–3gn组合的12 种工况，考虑3个主轴方向同时激励。

求解得到的干涉仪摆臂角位移和角速度均为时域瞬态过程，其时程曲线如图4。时程曲线包含了微振动作用的整个时域过程中引起的摆臂角度及角速度值信息。

最后将求得的控制系统和微振动引起的摆臂角度及角速度分析结果代入式（6）中，得到微振动条件下干涉仪摆臂摆动过程中光程差速度的时域值 v（ti），i=1，2，3，…，N，其中N为有限元时域离散的总时刻数。

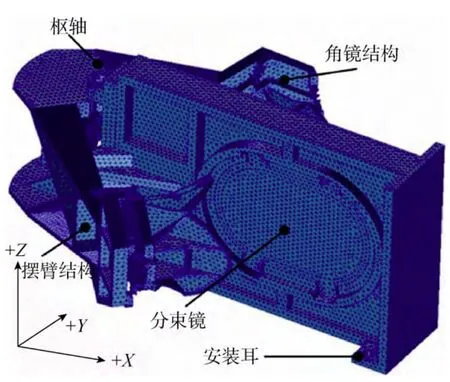
图3 某干涉仪结构有限元模型Fig.3 Finite element model of the interferometer

图4 离散时域分析结果Fig.4 Analysis results in discrete time sequence

于是，光程差速度的均值为

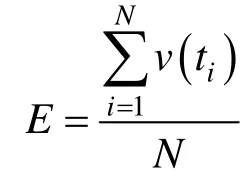
光程差速度的标准差为

上述各微振动工况条件下，光程差速度稳定度如表3所示。

表3 微振动条件下光程差速度稳定度Tab.3 Interferometer OPD speed stability under micro-vibration

分析表3 可得到以下结论，在一定控制系统下：

1）微振动频率一定时，振动加速度量级越小，稳定度越高。

2）微振动加速度量级一定时，振动频率越低，稳定度越高。

3）总体而言，当微振动幅值量级在10×10–3gn时，各频率下干涉仪光程差速度稳定度（1–α）均能满足＞99%的基本要求。

5 结束语

针对在轨微振动对光谱探测干涉仪机构精密运动的干扰问题，提出一种更全面的干涉仪光程差速度均匀性的分析方法。该方法将微振动引起的干涉仪结构响应作为一项影响因素，纳入到干涉仪稳定度的分析过程中，和通常的将外部激励的影响等效为某一影响因子的方法相比[10]，可以更真实地反映干涉仪在轨工作状态的可靠性。利用该方法能够在机构对外部环境激励控制算法不明确的条件下，快速给出干涉仪微振动量级的临界值。考虑到控制算法通常是对外部环境影响的改善，这一临界值具有一定安全裕度。因此该方法在解决实际工程问题方面具有一定的应用价值。

References)

[1]邢廷，龚惠兴.大气探测傅里叶变换光谱仪[J].遥感技术与应用,1999,14(1):5-10.XING Ting,GONG Huixing.Space Borne Fourier Transform Spectrometer for Atmospheric Sounding[J].Remote Sensing Technology and Application,1999,14(1):5-10.(in Chinese)

[2]沈中，葛之江，张连台.航天超光谱成像仪原理分析[J].航天返回与遥感,2002,23(2):28-34.SHEN Zhong,GE Zhijiang,ZHANG Liantai.The Principle of the Space Borne Hyper-spectrum Imager[J].Spacecraft Recovery and Remote Sensing,2002,23(2):28-34.(in Chinese)

[3]范东栋，王建岗，邬敏贤，等.用于遥感光谱探测的干涉成像光谱技术[J].航天返回与遥感,2001,22(4):52-57.FAN Dongdong,WANG Jiangang,WU Minxian，et al.Interferometric Imaging Spectrometer for Remote Sensing Spectral Sounding[J].Spacecraft Recovery and Remote Sensing,2001,22(4):52-57.(in Chinese)

[4]Jacques Giroux,Louis Moreau,Guillaume Girard，et al.Technological Evolutions on the FTS Instrument for Follow-on Mission to SCISAT Atmospheric Chemistry Experiment[J].Proceedings of SPIE,2010,7826:7826-1A.

[5]Hiroshi Suto,Akihiko Kuze,Kei Shiomi,et al.On Orbit Status of TANSO-FTS on GOAST[J].Proceedings of SPIE,2010,7826:7826-04.

[6]Brad Gom,David Naylor.Testing Results and Current Status of FTS-2,an Imaging Fourier Transform Spectrometer for SCUBA-2[J].Proceedings of SPIE,2010,7741:77412E-1.

[7]Francois Chateauneuf,Serge Fortin,Chantal Frigon,et al.ACE-FTS Test Results and Performance[J].Proceedings of SPIE,2002,4814:82-90.

[8]巫晓丽，范东栋，王平.空间大气成分探测傅里叶变换红外光谱仪[J].航天返回与遥感,2007,28(2):15-20.WU Xiaoli,FAN Dongdong,WANG Ping.Fourier-Transform Infrared Spectrometer for Space Atmospheric Component Detecting[J].Spacecraft Recovery and Remote Sensing,2007,28(2):15-20.(in Chinese)

[9]许家榕.高光谱干涉成像光谱仪研究[D].南京:南京理工大学,2008.XU Jiarong.On the High Optical Spectrum Interference Imaging Spectrometer[D].Nanjing:Nanjing University of Technology,2008.(in Chinese)

[10]贾晓山.红外光谱仪摆臂控制系统的研究[D].武汉:华中科技大学,2009.JIA Xiaoshan.On the Arm Scanning Control System of Infrared Spectrometer[D].Wuhan:Huazhong University of Science and Technology,2009.(in Chinese)