无人直升机非线性控制器设计

鲁 可，徐东杉

(中航工业直升机设计研究所，江西景德镇 333001)

0 引言

无人直升机是一种具有自主飞行和垂直起降能力的特殊飞行器，飞行控制系统是无人直升机的核心。无人直升机对象特性复杂、稳定性差、通道耦合严重、非线性特性强并且飞行模态较多，这对直升机的飞行控制系统提出了更高的要求。无人直升机飞控系统作为一个研究热点，引起了各国学者的广泛关注，并且取得了丰硕的成果。J.Gadewadikar运用静态输出反馈鲁棒控制方法设计了直升机的飞行控制系统，取得了良好的效果［1］。Nakwan Kim等运用自适应输出反馈方法设计了飞行控制系统，对直升机有一定的借鉴意义［2］。杨一栋教授作为国内较早研究直升机控制系统的学者，在其著作《直升机飞行控制系统》中提出了显模型跟踪系统，取得了较好的控制效果［3］。

1 反馈线性化理论

在非线性控制理论中，有两种常用的运算:李导运算数和李括号运算。下面将对这两种运算进行简单的介绍。

1.1 李导数运算

为了定义李导数，现给出一个光滑的标量函数h(x)及一个向量场f(x)，则该标量函数的李导数为该标量函数沿相应向量场的导数，称之为h对f的李导数。该导数是一个新的标量函数，记为Lfh。

多重李导数可以递归地定义为:

1.2 李括号运算

如果f(x)与g(x)为Rn上的两个向量场，两个同维的向量f(x)，g(x)的李括号运算定义为:

假设系统具有相对阶r，即:

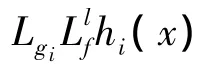
则原来的输出可以写成:

记为:

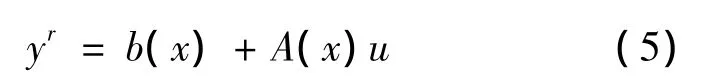
假设A(x)是可逆的，则可以得到逆系统的控制输入:

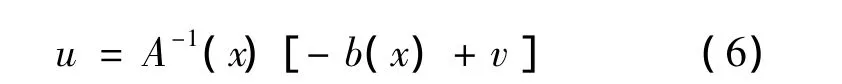
其中:b(x)为非线性输出状态，A(x)为非线性控制分布，参数v为期望的闭环系统动态性能特征。在该控制律作用下，闭环系统可以表达为:

2 直升机纵向非线性模型

直升机飞行高度随俯仰角的变化而变化，直升机动力学方程可以由下面的公式进行描述:

其中:

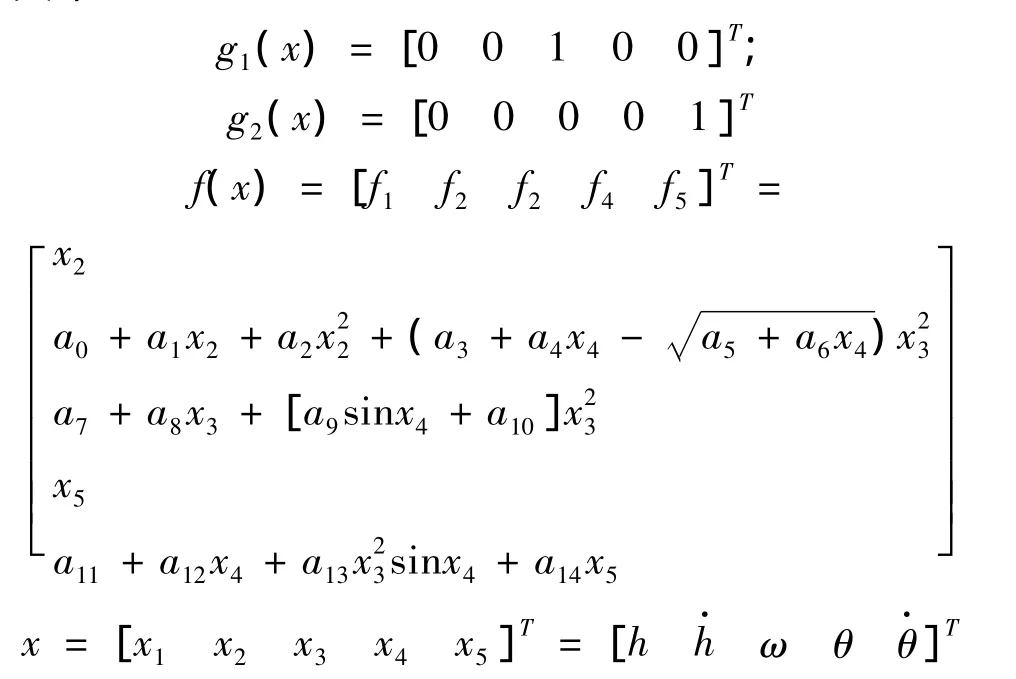
2.1 耦合性分析

假设直升机高度和俯仰角的初值为0，取油门控制输入为20，总距输入为0，直升机高度和俯仰角响应曲线如图1所示。

图1 油门输入下高度和俯仰角响应

取油门控制输入为0，总距输入为20，直升机高度和俯仰角响应曲线如图2所示。

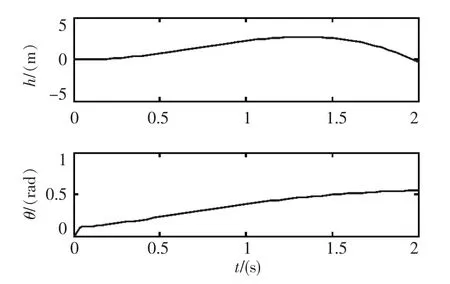
图2 总距输入下高度和俯仰角响应

从仿真结果可以看出，高度和俯仰角通道存在严重影响，耦合严重。

2.2 反馈线性化控制器设计

针对直升机模型进行反馈线性化，由反馈线性化理论可得:

设计控制律为:

现在选取高度通道进行进一步设计，经过反馈线性化，高度通道的伪线性系统可以近似用一个三阶积分环节来表示。现在用LQR方法对其进行设计，三阶积分系统的标准型实现为:

在进行LQR设计时，选择性能指标函数为:

R=1，于是得到状态反馈矩阵:

控制系统的结构框图如图3所示。

图3 飞控系统结构图

经过校正以后系统的阶跃响应如图4所示，可以看出控制系统的性能满足相应的要求。

图4 高度的阶跃响应

3 结论

本文针对无人直升机这一特殊控制对象非线性、强耦合等主要特点，首先根据非线性反馈线性化理论对其进行线性化处理，得到系统的伪线性系统，进而采用线性系统的设计方法设计最优控制器。通过仿真验证，该控制系统具有良好的性能。

［1］Gadewadikar J.H-infinity Static Output-Feedback Control for Rotorcraft［R］.AIAA－2006－6238.

［2］Kim N.Adaptive Output Feedback for High-Bandwidth Flight Control［J］.Journal of Guidance，Control，and Dynamics，2002，25(6):993 －1002.

［3］杨一栋，直升机飞行控制系统［M］.北京:国防工业出版社，2011.

［4］郭署山.无人直升机着舰控制技术研究［D］.南京:南京航空航天大学，2010.

［5］尹亮亮.无人直升机飞行控制若干关键技术研究［D］.南京:南京航空航天大学，2012.

［6］Gavrilets V.Nonlinear Model for a Small-Size Acrobatic Helicopter［R］.AIAA －2001－4333.

［5］Civita M L.Design and Flight Testing of a High-Bandwidth H∞Loop Shaping Controller for a Robotic Helicopter［R］.AIAA －2002－4836.

［7］Calise A J.Flight Evaluation of Adaptive High-Bandwidth Control Methods for Unmanned Helicopters［R］.AIAA－2002－4441.