铁路无缝线路温度应力的有限元分析
潘文彬,叶 渊,韩洪江,杨 韬,宋家旺*
(1.浙江工业大学 机械工程学院,浙江 杭州 310000;2.吉林大学 超塑性与塑性研究所,吉林 长春 130022)
0 引 言
无缝线路是将标准长度的钢轨焊接成长轨条并铺设到线路上,当环境温度发生变化时,由于轨枕等附属设施的存在,使得焊接长轨条不能进行自由伸缩,钢轨内部会产生巨大的温度应力,同时会破坏轨道结构。
无缝线路稳定性的研究始于德国。1902年德国科学家哈尔曼(A.Harrmann)首次讨论了无缝线路臌曲的可能性。我国一直十分重视无缝线路稳定性的理论研究工作。1977年以铁道科学研究院和长沙铁道学院为主的科研小组,在总结以往研究成果的基础上,提出了“统一无缝线路稳定性计算公式”[1-3]。罗雁云等[4-6]通过建立无缝线路轨道胀臌曲理论模型,分析无缝线路胀轨时的位移变化规律,研究温度应力作用下无缝线路轨道臌曲的变化特征以及轨道参数对其的影响。石现峰等[7]利用传热学的基本理论,采用有限元分析软件ABAQUS对板式无砟轨道结构在温度作用下的影响进行仿真计算,分析不同支撑形式及不同轨道板宽度和厚度对无砟轨道结构温度效应的影响。此外,国内外学者在分析无缝线路稳定性方面做了大量的工作,并取得了一定的成果[8-12]。
本研究以无缝线路臌曲理论为依据,结合有限元方法,利用大型有限元分析软件ABAQUS对无缝线路进行温度应力的分析研究。
1 有限元分析
1.1 钢轨模型的建立
本研究参考的无砟轨道模型如图1所示[13]。
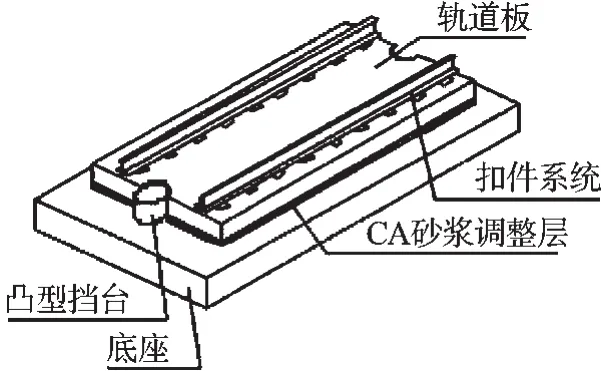
图1 I型板式无砟轨道结构示意图
由于ABAQUS的建模功能并不强大,笔者使用三维建模软件CATIA建立模型,再将模型导入ABAQUS。钢轨的模型选择60 kg/m轨型。
无缝线路模型的参数取值如表1[14-15]所示。本研究主要针对钢轨内部温度应力的变化,轨道板及其底座的物理参数数非常接近,故在模型中将轨道板和底座简化在一个模型中。由于每组扣件都对钢轨的垂向、纵向以及横向运动限制,笔者将每个扣件简化为3个弹簧单元。钢轨与轨道板的连接主要通过3个组模拟扣件的弹簧连接。
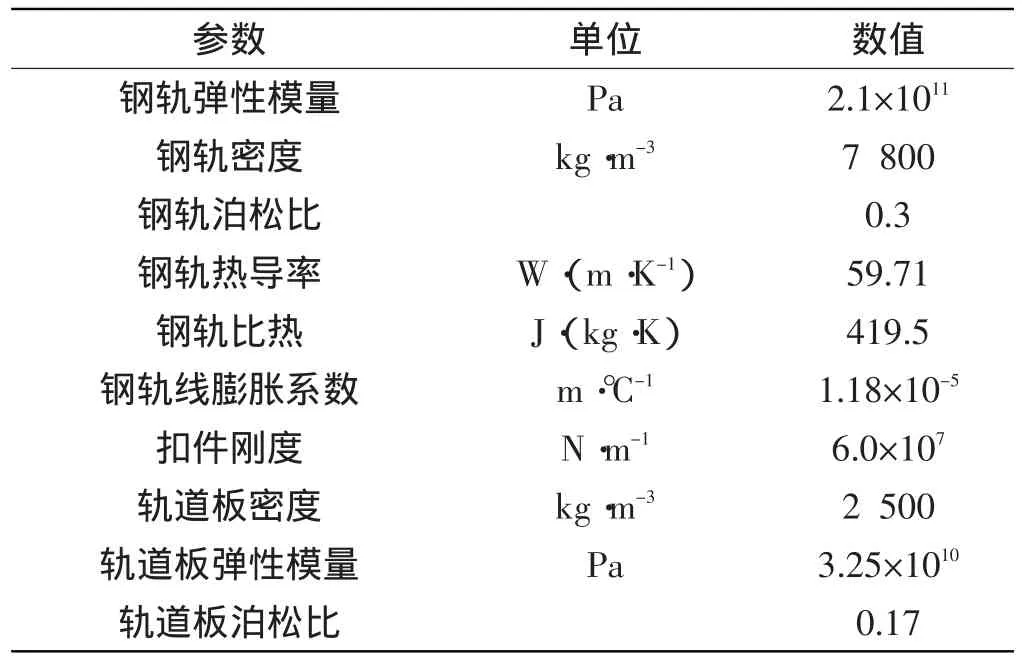
表1 无缝线路模型力学性能和材料参数
无缝线路模型如图2所示。

图2 初始无缝线路模型
1.2 有限元分析过程
结合文献[1]可得到钢轨温度变化数值,分析过程主要分为3步:
(1)建立钢轨模型的初始边界条件。初始边界条件分为两个部分,其一是初始温度场,即钢轨的锁定轨温,这里取22℃。
(2)模拟气温上升到最高气温。最高轨温取值62.7℃,模拟钢轨轨温上升到相应的温度,并输出最高轨温时钢轨的温度应力截图。
(3)模拟气温从最高点下降至最低气温-27℃,钢轨轨温也降至相应的最低点,并输出钢轨模型的温度应力。
1.3 有限元分析结果
本研究采用有限方法对得到的结果进行分析[16-17],取模型中间的中心的一截钢轨,钢轨与扣件接触面位于底面正中间,在轨温最高点的温度应力模型如图3所示。从图3中可以看出,温度应力最大处主要集中在扣件所在位置,应力集中区域沿着扣件逐渐减小。

图3 最高轨温下无缝线路的mises应力图
由于mises应力适用于第4强度理论,而无缝线路中的钢轨材料为脆性材料,多用第1强度理论,即只考察最大主应力,本研究继续对各向应力分量进行讨论。
由于扣件、轨道板等基础设施的约束,温度变化时钢轨将不能自由伸缩。因而无缝线路中最危险的就是钢轨纵向温度应力,纵向温度应力分布如图4、图5所示。钢轨纵向温度应力最大点位于扣件与钢轨接触面积边缘,以最高轨温为例进行分析(如图4所示):由于扣件的直接约束,使得钢轨与扣件接触面不能自由膨胀,在接触面受到压应力时,最大值为164.9 MPa,同时导致接触面左右两端的钢轨底面受到过大的纵向拉应力,最大值为131.7 MPa。同理可得图5中纵向温度应力最大压应力为158.5 MPa,拉应力为198.5 MPa。由于纵向钢轨温度应力对无缝线路影响最大。查文献[1]得无缝线路钢轨强度为457 MPa。经比较得,纵向温度应力满足钢轨强度。
无缝线路钢轨切向温度应力分布图如图6、图7所示。以最高轨温为例(如图6所示),轨温升高时,由于扣件的约束,钢轨与扣件接触面积处为应力最大区域,最大值压应力为165.1 MPa。图7中最大拉应力为198.7 MPa。
无缝线路中钢轨的垂向温度应力分布如图8、图9所示。以图8为例,轨温升高时,应力集中区域还是位于扣件与钢轨接触面上,沿着接触面积的轮廓分布,最大温度应力值为219.4 MPa。在图9中,轨温降低,温度应力最大值为264.2 MPa。
2 结束语

图4 最高轨温时钢轨纵向温度应力分布图

图5 最低轨温时钢轨纵向温度应力分布图
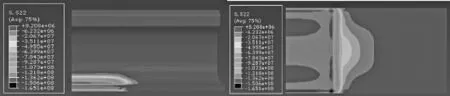
图6 最高轨温时钢轨切向温度应力分布图

图7 最低轨温时钢轨切向温度应力分布图
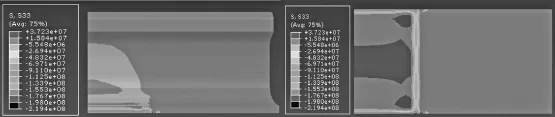
图8 最高轨温时钢轨垂向温度应力分布图

图9 最低轨温时钢轨垂向温度应力分布图
本研究以无砟轨道为理论模型,考虑了扣件、轨道板等附属设施的约束,并按照对应的材料参数,完成了无缝线路的有限元建模,在轨温升降的基础上,得到了相应的温度应力分布模型图。通过进一步分析mises应力、纵向、切向和垂向的温度应力分布图,得到了钢轨在轨温变化时钢轨的受压以及受拉应力部位,并在图像中显示出来。根据第一强度理论得出:温度变化时钢轨内部最大应力为纵向温度应力,并且经过比较,该应力满足钢轨强度。
笔者的研究工作为进一步研究无缝线路温度应力打下了基础,提供了一定的思路。但在模型上还具有一定的局限性,以后的研究工作将在此基础上继续完善轨道模型,不断深入研究。
(References):
[1] 广钟岩,高慧安.铁路无缝线路[M].4版.北京:中国铁道出版社,2005.
[2] KISH A,SAMAVEDAM G,JEONG D.Analysis of Thermal Bucking Tests on U.S.Railroads[R].Technque Report,NTISPB83-203554,1982:21-102.
[3] JEONG D,SAMAVEDAM C,KISH A.Determination of Track Lateral Resistance from Lateral Pull Tests[R].Final Report,NTIS-PB86-225612,1986:1-49.
[4] 金寿延,朱剑月,罗雁云,等.无缝线路轨道的温度力与振动特性关系的研究[J].机械强度,2002,24(1):144-147.
[5] 罗雁云,施董燕,谭晓春.纵向力作用下无缝线路动态特性有限元分析[J].力学季刊,2008,29(2):284-290.
[6] 罗雁云,李振廷.轨道参数变化对无缝线路稳定性影响[J].中国铁道科学,2008,29(2):34-36.
[7] 石现峰,李建斌.温度对板式无砟轨道结构的影响研究[J].铁道工程学报,2008(5):30-32.
[8] DAXUN T.Distribution of Temperature Stresses along the Continuouslv Welded Track[R].American Railroad Engi⁃neering AssociaLion,Bulletin 692,1983:35-51.
[9] 张 斌,雷晓燕.基于车辆-轨道单元的无砟轨道动力特性有限元分析[J].铁道学报,2011,33(7):78-85.
[10] 雷晓燕.轨道力学与工程新方法[M].北京:中国铁道出版社,2002.
[11] 童大埙.铁路轨道[M].3版.北京:中国铁道出版社,1996.
[12] 钟方千,周小林,褚卫松.无砟轨道无缝道岔温度纵向力研究[J].山西建筑,2008,34(18):24-25.
[13] 李中华.CRTSⅠ型与CRTSⅡ型板式无砟轨道结构特点分析[J].华东交通大学学报,2010,27(1):22-28.
[14] 李 伟,温泽峰,金学松,等.滚滑接触下钢轨热力耦合分析[J].工程力学,2010,27(8):199-205.
[15] 李春霞,殷明旻,车晓娟.路基上无砟轨道机床反力系数取值的探讨[J].铁道建筑,2009,27(8):199-205.
[16] 陈乐平,单 磊,陈 罡.基于Moldflow和ANSYS的防眩板有限元分析[J].轻工机械,2012,30(1):5-9.
[17] 石亦平,周玉蓉.ABAQUS有限元分析实例讲解[M].北京:机械工业出版社,2006.

