冷轧过程板形翘曲行为的控制

供稿|丁荣杰,柯可力, 郑涛, 张清东, 张晓峰, 章培成 / DING Rong-jie, KE Ke-li, ZHENG Tao,ZHANG Qing-dong, ZHANG Xiao-feng, ZHANG Pei-cheng

内容导读

翘曲作为板带材板形缺陷之一,越来越受到专家和学者的重视和关注.目前对于翘曲的研究主要集中于平整与拉矫等精整工序,而对于冷轧过程中产生的带钢翘曲问题并没有特别好的控制和应对改善方法.沿厚度方向的延伸不均匀是导致翘曲产生的主要原因.而轧制过程中出现的不对称是导致厚度方向延伸不均匀的直接原因.本文运用有限元软件建立了二维轧制模型,分析了在不对称轧制时带钢的力学行为变化,对翘曲的产生机理进行了研究,提出了有效控制轧制过程中带钢翘曲的方法.

在不锈钢的生产过程中,翘曲问题日益成为制约其板形质量提高的一个重要瓶颈[1].某钢厂生产BA光亮板时,将轧制后的带钢经过光亮退火线中的马弗炉时,由于带钢存在较大的槽沟,在马弗炉入口和出口处容易与槽口产生刮伤,造成马弗炉的磨损以及带钢表面的刮痕,严重影响了光亮退火线的正常生产,大大降低了带钢 表面质量.此外轧制过程中带钢产生的翘曲加大了后续精整工序的难度,还会增加后续精整工序矫正板形的成本,如加剧了拉矫机轧辊和平整机轧辊的磨损.

带钢在生产过程中沿厚度方向的延伸不均匀是导致翘曲产生的主要原因[2-3].上下表面延伸不一致会使正、反两面的残余应力也不一样,沿正、反两面残余应力的分布及大小决定了样板弯曲的方向和程度[4].轧制过程中非对称轧制因素的存在是导致上下表面延伸不一致的直接原因[5-7].因此本文针对轧制过程中的不对称因素,对带钢表面的延伸差进行了分析.

由于需要考虑沿带钢厚度的应力应变情况,就不能将带钢简化成壳单元进行分析,进行实体单元的分析,因此加大了分析的难度.本文通过运用ABAQUS软件建立的轧制过程有限元模型来进行分析.

基于平面应变的轧制过程有限元模型的建立

考虑到实际轧制时只有上下工作辊和带钢进行接触,工作辊直接作用于带钢,下压而引起带钢长度方向的延伸,因此将有限元模型简化为上下两工作辊和带钢,如图1.

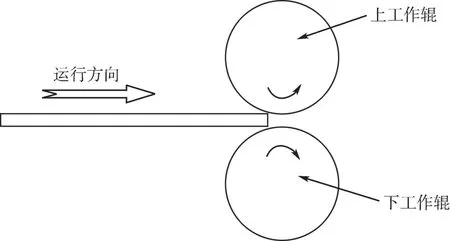
图1 轧制模型简化图

实际带钢的长度很长,为简化模型,减少计算.选取带钢的几何尺寸为1000 mmX4 mm,沿厚度方向设置6个单元,长度方向100个,总共600个单元.考虑到模型中存在接触,尽量采用一阶单元,在模型中,带钢有较大的变形,线性缩减积分单元能够很好地承受扭曲变形,因此本模型中单元类型设置为平面应变线性缩减积分4节点单元CPE4R.为兼顾计算的精度和速度,将工作辊靠近辊面部分进行局部细化200X5,其余部分进行沿径向逐步变疏的自由网格划分,单元总数为1707.单元类型为线性缩减积分四节点单元CPE4R.将建立的两个工作辊和带钢进行装配,如图2所示.

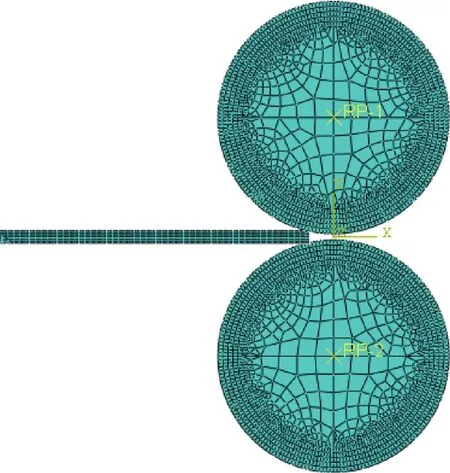
图 2 轧制模型

考虑到实际情况,工作辊的刚度较大,其变形为弹性变形,因此将工作辊设置为弹性体,E=210 GPa,υ=0.3;带钢在长度方向和厚度方向具有较大的弹塑性变形,因此需要设置带钢的弹塑性特性.本课题研究的带钢材料为304钢,采用的本构关系曲线如图3,E=210 GPa,υ=0.3.

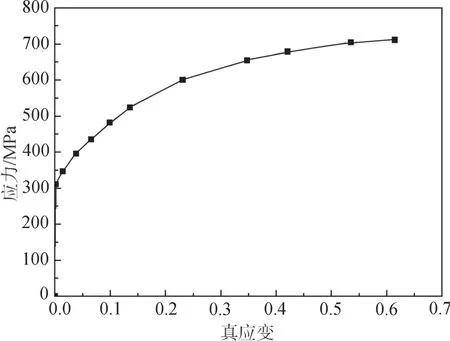
图 3 304钢种的带钢单轴拉伸应力-应变关系

将带钢的轧制过程分为两步:第一步,带钢头部强制咬入 (带钢自身具有速度),直到基本咬入;第二步,去除带钢自身速度,完全轧辊的转动,由于摩擦力作用使带钢向前运行.

建模时,需定义两对接触.上工作辊表面与带钢上表面接触,由于上工作辊的刚性较大,因此选取上工作辊表面为主面,带钢上表面为从面;下工作辊表面与带钢下表面接触,定义下工作辊表面为主面,带钢下表面为从面.

两对接触均采用摩擦模型:

式中,f为摩擦应力,MPa;μ为摩擦因数;p为接触应力,MPa.

为保证带钢在轧制过程中出现整体的刚性位移,在带钢端部中心节点添加厚度方向的约束,第一步中,在带钢尾部添加速度约束,在第二步时去掉.限制两工作辊水平和垂直方向的位移,并给定转动速度.至此基于平面应变的有限元模型建立完毕.

根据建模步骤进行建模,最后得到仿真计算结果.如图4所示为在稳定轧制过程时带钢内部的Mises应力.从图中可以看到变形区的应力最大,达到了470 MPa.

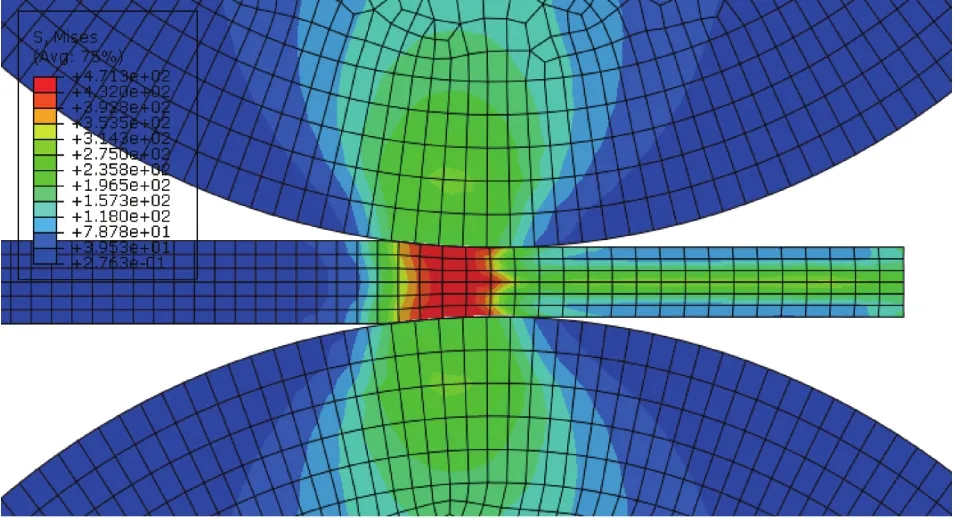
图 4 带钢稳定轧制过程Mises应力分布云图

带钢的轧制过程分为头部咬入阶段也即带钢填充辊缝的阶段和稳定轧制阶段,在头部咬入阶段,作用在轧辊上的轧制力逐步增大,此后到达稳定轧制阶段,轧制力的大小基本趋于一致,如图5所示,稳定轧制时的轧制力大小在4500 kN左右,与现场实测的轧制力基本相近.因此,该二维模型分析带钢在轧制过程中的变形是可行的.

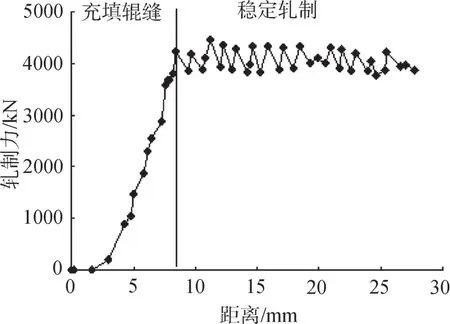
图 5 轧制力随轧制过程的变化

仿真结果分析

翘曲产生的根本原因:轧制过程中非对称因素的影响是导致带钢沿厚度方向产生不均匀变形的直接原因.带钢的塑性变形(主要是纵向延伸)在厚度方向(铅垂方向)上的不均匀导致了上下表面受力不一致,此不均匀的受力在厚度方向上产生了一个转动力矩,由于在轧制生产线上带钢在长度方向上不能发生转动,因而只会出现C翘的情况;当带钢剪切后,此时长度方向的转动自由,在力矩的作用下会产生L翘或者四角翘的情况.

轧制过程中非对称因素主要包括:带钢上下表面润滑不一致和工作辊粗糙度差异导致的上下表面摩擦因数不一致;上下二中间传动辊辊径差异导致的上下工作辊线速度不一致;轧制线高度变化引起的传送角的存在,导致上下工作辊包角不一致;上下工作辊径差异.

图 6 表面摩擦因数不同时带钢沿厚度方向的应力应变分布(上摩擦因数μ上=0.2,下摩擦因数μ下=0.1)

带钢上下表面摩擦因数不一致时,上下表面沿接触弧长的轧制力的分布也会出现不一致,如图6(a)所示.由于上表面的摩擦因数为0.2,下表面的摩擦因数为0.1,从图6(b)可以明显看出带钢上表面摩擦力幅值大于下表面摩擦力.由于摩擦的不一致,从图6(c)的放大图中可以看出,上表面的中性点在下表面的中性点的左侧0.1 mm处,中性面发生倾斜,形成剪切带,上表面的前滑区的长度要比下表面大,也就是上表面受到的摩擦阻力的区域长度比上表面要大,因此上表面的材料流动受到的阻力比下表面要大,下表面材料的流动比上表面要快,使得上表面的塑形延伸小于下表面的塑性延伸,如图7(a)所示.又由于在轧制过程中,带钢受到张力作用,延伸大的部分受到的纵向应力就小,如图7(b)所示带钢沿厚度方向的纵向残余应力也是不均匀的,上表面的残余应力比下表面的残余应力大20 MPa左右.去除张力后,离线带钢呈现上翘.

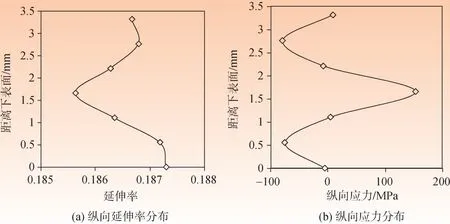
图 7 摩擦不同时轧后带钢沿厚度方向纵向应力应变分布

根据所建立的轧制过程有限元仿真模型,对各非对称轧制因素进行工况计算,如表1所示.并对各因素对翘曲的影响规律进行分析.

表1 非对称轧制因素工况表

◆ 摩擦因数

带钢上表面与工作辊之间的摩擦因数大于下表面之间的摩擦因数,此时延伸差为负值,沿纵向的残余应力差为正值,带钢向上弯曲,且随着上下摩擦因数差距的增大,翘曲量也随之增大.

摩擦因数小的表面产生的延伸率较大,带钢向摩擦因数大的方向弯曲,如图8.

◆ 上下辊速度不一致

从图9中可以看出,上辊辊速小于下辊辊速时,带钢上下表面延伸率差值为负值,残余张应力为正值,带钢向上弯曲,且随着辊速差的增大,延伸差也随之增大.

辊速高的相应表面产生的延伸率大,带钢向辊速小的方向弯曲.

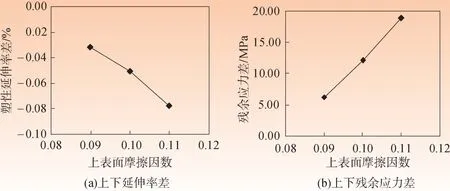
图8 下表面摩擦因数为0.08,上表面摩擦因数 0.09、0.10和0.11

图 9 下辊速度为290 m/min,上辊小于下辊速度1.5%、1%和0.5%

◆ 上下辊辊径不一致

由于上下辊表面线速度一致,上辊直径小于下辊直径,此时上辊的压下大于下辊的压下,上表面的延伸率大于下表面的延伸率,带钢向辊径大的方向弯曲.从图10中可以看出,带钢上下表面的延伸率差值为正值,且随着上辊直径越来越接近下辊直径,翘曲减小.

工作辊表面线速度一致时,带钢向直径大的方向弯曲,且上下辊差值越大,产生的翘曲值也越大.

◆ 上下辊偏移距离

负值为上辊向入口处偏移,正值为向上辊出口处偏移.

上工作辊偏向入口侧,带钢向下弯曲;上工作辊偏向出口侧,带钢向上弯曲.

如图11所示,当上工作辊偏向入口侧时,带钢上下表面的延伸率差为正值,残余应力差为负值,此时表现为下扣翘曲缺陷,当偏移距离变小时,延伸率差和残余应力差又减小,知道上下辊处于同一条垂直线上时,上下对称差值为零;当上工作辊偏向出口侧时,刚好相反,带钢表现为上翘缺陷.

图 11 上下辊存在水平偏移

◆ 轧制线高度

轧制线高度会影响带钢翘曲的程度,且随着轧制线高度的增大,其上下表面的延伸率差和上下残余应力差也随之增大 (图12).但是,从值上来看轧制线高度达到最大7 mm时,上下表面延伸率差值只有0.01016%,残余应力差值只有-4.09 MPa,相比较其他因素而言影响较小.

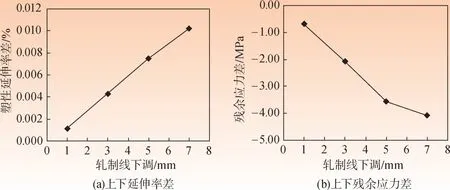
图 12 轧制线高度变化

因此,轧制线高度对带钢翘曲影响较小.

现场应用

针对实际生产中较易出现下扣的翘曲缺陷,结合有限元仿真分析提出了有效消除和抑制下扣的翘曲缺陷的方案.

(1) 增大上表面的摩擦因数或者减小下表面的摩擦因数.减小上表面的润滑油喷淋量,上辊采用粗糙度较大的轧辊,以此来增大上表面的摩擦.

(2) 上工作辊向出口偏移.辊系配辊时,上半辊系左侧一中间辊辊径大于右侧一中间辊辊径,或者通过支持辊侧偏心刻度进行调节.

(3) 上工作辊线速度小于下工作辊.本文研究的20辊森吉米尔轧机由单电机传动四个二中间传动辊,再通过辊间摩擦将力矩传动到工作辊,因此可使上半辊系中的二中间辊直径大于下半辊系来提供速度差.

(4) 上工作辊辊径大于下工作辊的辊径.

其中对方案 (2) 进行了现场相关实验,实验结果如表2所示.槽沟的现场检测方法如图13所示.根据现场统计,正常轧制时带钢槽沟值在下扣40 mm左右,从表中可以看出,当上工作辊向出口侧偏移,采用奇数道次,带钢的翘曲有了较大的减小,轧后槽沟值在+20 mm上翘值;采用偶数道次,带钢的翘曲有了较大的减小,减小为-20 mm左右.因此采用奇数道次和偶数道次合理的偏移量均能减小翘曲.

图13 现场槽沟检测

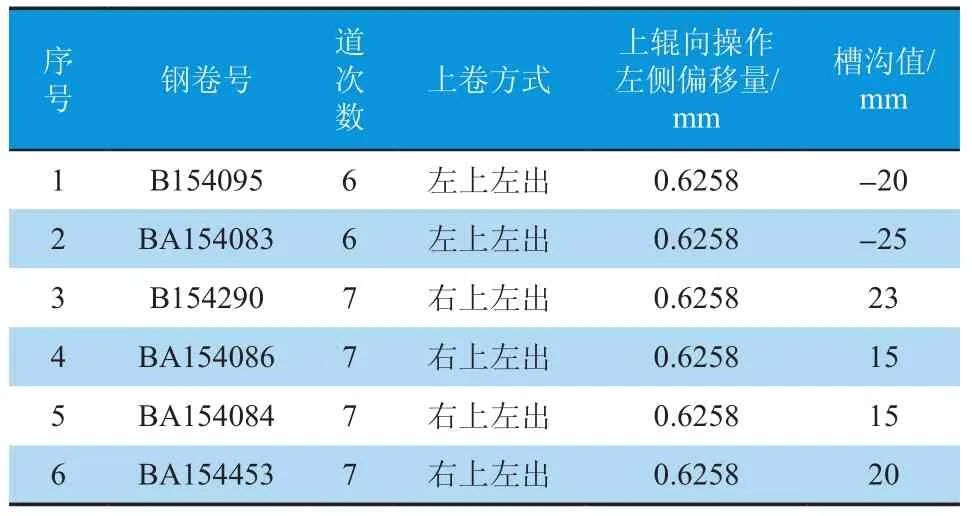
表2 现场翘曲实验结果

结束语

本文针对冷轧过程中产生的翘曲问题,以有限元仿真为手段对轧制过程进行了仿真建模,分析了不对称轧制导致翘曲产生的内在机理,以延伸差为主要研究内容,研究了不对称轧制因素对翘曲的影响规律,得到以下结论:

(1) 不对称轧制会引起上下表面沿接触弧长摩擦应力不一致,使中性面产生倾斜,形成剪切区域,从而导致翘曲产生.

(2) 带钢向摩擦因数大,辊速小,辊径大的方向弯曲,向靠近出口侧的轧辊方向弯曲,对于森吉米尔轧机,轧制线高度对翘曲影响较小.

(3) 提出了现场消除翘曲的方法,在实际应用中,通过调节上下轧辊偏移量有效地控制了翘曲的产生.

[1] Mucke G, Karhausen K F,Putz P D.Methods of describing and assessing shape deviation in strips.MPT International, 2002(3):58-65.

[2] 魏立群, 柳谋渊, 张杏耀, 等.平整轧制中轧件L弯成因分析与及对策.轧钢, 2003, 20(2): 20-22.

[3] Mousavi S A A, Ebrahimi S M, Madoliat R. Three dimensional numerical analyses of asymmetric rolling. Journal of Materials Processing Technology, 2007, 187-188: 725-729.

[4] 何建锋. 宝钢镀锡板翘曲原因分析与对策. 宝钢技术, 2004 (1):36-39.

[5] Knighta C W, Hardy S J. Investigations into the influence of asymmetric factors and rolling parameters on strip curvature during hot rolling. Journal of Materials Processing Technology, 2003,134(2):180-189.

[6] Jiang Z Y, Tieu A K. A 3-D fi nite element method analysis of cold rolling of thin strip with friction variation.Tribology International,2004, 37(2):185-191.

[7] Ji Y H, Park J J. Development of severe plastic deformation by various asymmetric rolling processes. Materials Science and Engineering,2009, 499(1-2): 14-17.