具阶段结构两种群竞争模型的最优捕获

颜未霖

（兰州交通大学数理学院，甘肃 兰州 730070）

具阶段结构两种群竞争模型的最优捕获

颜未霖

（兰州交通大学数理学院，甘肃 兰州 730070）

对一类具有阶段结构的两种群竞争模型进行了分析，讨论了该系统正平衡点的局部稳定性，得到了该系统唯一正平衡点全局渐进稳定的条件，由最优控制理论获得了最优捕获策略。

竞争；阶段结构；全局渐进稳定；最优捕获

近年来有关具有两阶段结构的单种群模型研究的文献较多，文献[1]列举了部分学者的研究成果。目前对具有三阶段结构的单种群模型的研究文献[2-3]也较多。但是对具有两阶段结构的两种群模型研究成果较少。文献[4]对具有两个阶段结构的单种群模型进行了分析，把单种群分为成熟和不成熟两阶段，在此基础上，我们对此模型做了更进一步的改进，建立了具有阶段结构的两种群竞争模型。

我们假设A种群具有阶段结构，把A分为两个阶段：成熟和不成熟，仅有成熟种群具有生育能力，建立的模型如下：

满足初始条件x1（0）＞0,x2（0）＞0,y（0）＞0。其中：x1,x2分别代表不成熟和成熟的A种群在t时刻的种群密度；y表示B种群在t时刻的种群密度；r1, r2,r3表示死亡率；s表示B种群的内禀增长率；d1表示A种群的出生率；d2表示A种群由不成熟阶段到成熟阶段的转化率；α,β分别表示成熟阶段的A种群和B种群间的竞争程度；E表示对成熟阶段的种群A的捕食程度；q为捕获系数；k1,k2,k3分别为密度制约项。系统（1）中的系数均为正常数。

1 正平衡点分析

记

m1=r1+d1,m2=r2+qE,m3=s-r3＞0,正系统（1）可化简为

显然，曲线L1,L2为抛物线。现在假设K1,K2表示L1,L2在（0，0,0）处的切线率。

1）当k2k3-αβ＜0,K1＞K2时，系统（3）在第一象限内有唯一的交点。

2）当k2k3-αβ＞0,K1＜K2时，系统（3）在第一象限内有唯一的交点。

3）当k2k3-αβ=0,系统（3）在第一象限内有唯一的交点。

初到新疆，尽管有心理准备，但西北戈壁的干旱气候还是让刘宇星鼻子时常流血、突如其来的饮食结构和孤身一人的团场生活让他这个土生土长的抚顺人有些茫然。但想到组织的信任与家人的嘱咐，刘宇星迅速克服了气候不适、心理不适和饮食不适等，充满激情地投入到工作中。

我们让

系统（4）在平衡点处的雅克比行列式为

系统（4）在平衡点处的特征方程为

λ3+a1λ2+a2λ+a3=0,

其中：

然后我们构造Liapunov函数则有：

2 最优捕获策略

系统（2）中：x1（t）,x2（t）,y（t）为状态变量；E（t）为控制变量，0≤E（t）≤Emax。

首先我们构造哈密顿函数

这里λ1（t）,λ2（t）,λ3（t）是伴随变量，伴随方程为：

从伴随方程（6）可得到

其中：

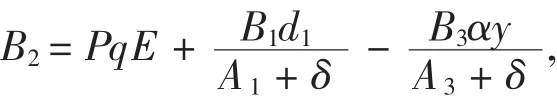
由式（9）可得

又式（8）和式（10）可得：

[1]陈兰荪,王东达,杨启昌.阶段结构种群动力学模型[J].北华大学学报：自然科学版,2000,1（3）：185-191.

[2]梁志清,赵强.一类具三阶段结构的单种群的最优收获策略[J].玉林师范学报：自然科学版，2005,26（3）：1-3.

[3]潘红卫,梁志强.非线性生育率阶段结构种群模型的全局渐进稳定[J].广西师范学院院报：自然科学版,2004,21（2）：22-25.

[4]Wang Jing,Wang Ke.The Harvesting Problemsofa Stage-Population[J].Applied Mathematicsand Computation,2004,148：235-247.

[5]马知恩,周义仓.微分方程的定性分析和稳定性方法[M].北京：科学出版社,2001.

[6]Clark CW.Mathematicional Bioeconomics.The Optimal Control of Renewable Resource[M].New York：John Wiley＆Sons Inc,1990.

〔责任编辑 高 海〕

Optimal Harvesting of Two Species Competitive Modelw ith a Stage-structure

YANWei-lin
（School of Mathematics,Lanzhou Jiaotong University,Lanzhou Gansu,730070）

A class of two species and competitivemodelwith a stage-structure is considered.The local stability of the unique the positive equilibrium are discussed.Some conditions for global asymptotic stability of the unique positive equilibrium are obtained.The optimal harvesting strategy is gained by the optimal control theory.

competitivemodel；stage-structure；globally asymptotical stability；optimal harvesting

O212.4

A

2013-08-11

颜未霖（1987-），男，甘肃兰州人，硕士，研究方向：生物数学。

收稿日期：2013-07-20

作者简介：员宁波（1982-），男，山西平陆人，硕士，讲师，研究方向：财务管理。

1674－0874（2013）05－0013－04