可逆三分子反应模型的系统分析

孔丽丽

（山西大同大学数学与计算机科学学院，山西 大同 037009）

可逆三分子反应模型的系统分析

孔丽丽

（山西大同大学数学与计算机科学学院，山西 大同 037009）

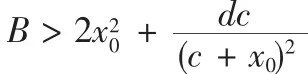
生化反应；极限环；存在性

1 建立模型

由文献[1]我们知道：在生物化学反应中,反应物的反应速度能近似地看作与其浓度成正比,但是反应物并不随着其浓度的增多而无限增大。即当其浓度超过一定的量后,反应速度并不加快了，也就是说它有一个饱和反应速度。文献[2]讨论了一类可逆三分子反应模型，得到该模型奇点的性态以及极限环的存在性。在文献[2-4]基础上讨论一类具有一级饱和反应速度的可逆三分子反应模型

其中A＞0，B＞0,c＞0,d＞0。基于系统（1）的实际意义,限制在区域Ω={（x,y）｜x≥0,y≥0}内进行分析。

2 奇点的类型

易知，当d＞A时,系统（1）在Ω内有唯一的奇点R（x0,y0）,其中

以下均讨论d＞A的情形，我们有：

证明由系统（1）在R处的变分矩阵即可证明得到该结论。

3 正解的有界性

定理1系统（1）的一切正初始值的解得正半轨线有界。也就是说存在闭折线Γ使得对任意Μ（x1, y2）∈intΓ,当t增加时,系统（1）的从M出发的轨线跑不出Γ所围的区域。

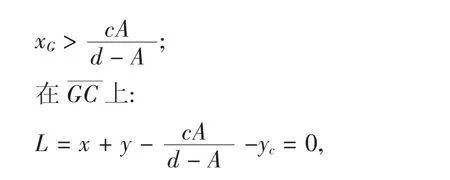
4 极限环的存在性

证明利用Bendixson环域定理来构造广义的Bendixson环域。其外境界线为定理1中证明得到的闭折线Γ=CDEˆFGC,而正平衡点R在定理2的条件下为不稳定的焦点或结点,于是在区域Ω的内部正平衡点R的外部系统（1）至少存在一个稳定的极限环。定理得证。

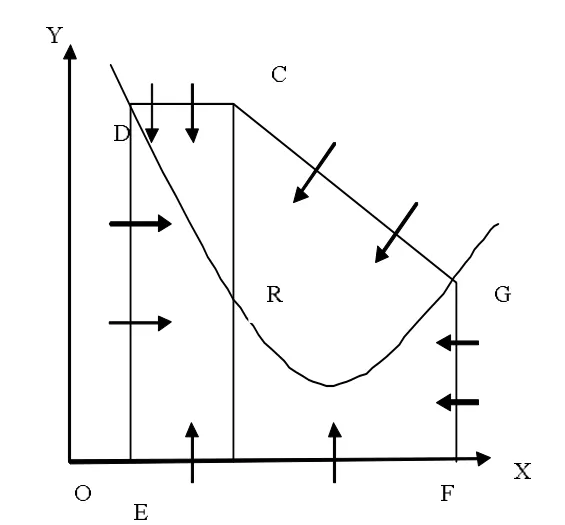
图1 Bendison环域

[1]陈兰荪,陈健.非线性生物动力系统[M].北京：科学出版社,1993.

[2]贾建文.可逆三分子反应模型的系统分析[J].生物数学学报,1999,14（4）：415-418.

[3]孔丽丽,贾建文.一类多分子生化反应系统的定性分析[J].山西师范大学学报：自然科学版,2012,26（1）：21-24.

[4]陈慧琴.一类含强迫项的二阶微分方程解的振动性[J].山西大同大学学报：自然科学版,2011,27（4）：5-6.

〔责任编辑 高 海〕

Systematic Anlysis of a Model for Reversible Trimolecular Reaction

KONGLi-li

（School of Mathematicsand Computer Science,Shanxi Datong University,Datong Shanxi,037009）

In this paper,a model in biochemical reaction is discussed,by means of the ordinary differential equation qualitative method,we obtain such conclusions as boundedness of solutions which initial value is in the first quadrant and the existence of limit cycle.

biochemical reaction；limit cycle；existence

O175

A

2013-06-04

孔丽丽（1984-）,女,山西吕梁人,硕士,助理实验师,研究方向：生物数学。

1674-0874（2013）05-0025-03

收稿日期：2013-08-19

山西省高等学校科技研究开发项目[20121015]；国家自然科学基金资助项目[11271235]

作者简介：孟献青（1979-）,女,山西怀仁人,硕士,讲师,研究方向：图论与高等数学。