基于Pushover理论的钢管混凝土构件塑性铰特性值研究

吝红育

(西安科技大学建筑与土木工程学院，陕西西安710054)

0 引言

随着西部大开发战略的实施和交通建设的发展，能够适应西部复杂地形地貌的新型大跨、重载桥梁结构不断出现.主梁和桥墩采用钢管混凝土桁架结构的高墩大跨连续梁桥是桥梁发展的一个新方向，2012年建成的雅西高速干海子特大桥就是该类结构的典型代表.目前，对钢管混凝土桁架和节点的研究相对较多，并取得了一系列的研究成果;对钢管混凝土桁架梁桥的力学性能也有少量的的研究，但其理论和成果并不完善，特别是梁桥在弹塑性阶段静、动力性能的研究几乎空白，这极大的制约着该类新型桥梁的建设和发展［1-6］.

Pushover理论是目前较为实用的结构弹塑性简化分析方法，广泛应用于结构弹塑性地震分析，也可用于结构极限承载力和失效薄弱点分析，关键在于塑性铰特性值的确定.现有构件塑性铰特性值主要基于两本手册［7-8］:混凝土塑性铰的性能指标来自于《混凝土建筑抗震评估和修复》(ATC—40);钢结构塑性铰的性能指标来自于《房屋抗震加固指南》(FEMA365).钢管混凝土构件塑性铰特性值是将其混凝土构件等效为钢件或钢筋混凝土构件，按等效材料定义塑性铰特性值，这显然与构件实际的力学性能不同［9］.

笔者以钢管混凝土统一理论本构关系为基础，对钢管混凝土构件塑性铰特性的取值进行讨论，并与钢管混凝土桁梁简支梁桥的模型试验结果对比，为大型钢混组合混凝土桁架梁桥在弹塑性阶段静、动力性能研究提供理论基础和研究手段.

1 塑性铰本构关系

塑性铰本构关系一般由构件的恢复力特性描述，常用的塑性铰的特性值曲线如图1所示.纵坐标的力代表弯矩、剪力、轴力;横坐标的位移代表曲率或者转角、剪切变形和轴向变形.整个曲线分为弹性阶段AB、弹塑性阶段BC、刚度陡降阶段CD和残余强度阶段DE，其中B点表示出现塑性铰，C点为倒塌点.B点的确定，涉及到杆件屈服力和屈服位移的确定;C、D及E点的纵、横坐标需要分别按照力、位移与屈服力和屈服位移的比值来输入.ATC—40中将弹塑性阶段的状态再分为直接居住极限状态IO、安全极限状态LS、倒塌极限状态CP.

2 塑性铰特性值推导

2.1 钢管混凝土M铰

图1 塑性铰本构关系Fig.1 Constitutive relationship of plastic hinge

钢管混凝土构件受弯的M-φ曲线，如图2所示.该曲线分为弹性阶段OA、弹塑性阶段AB、强化阶段BC.①弹性阶段:曲线基本呈直线，受压区钢管处于弹性工作状态，钢管与混凝土之间在A点时的紧箍力不大，可认为钢管和混凝土均处于单向受压状态;受拉区钢管的横向变形受到内部混凝土的限制，处于三向应力状态，而混凝土不承担拉应力，对钢管起横向约束作用，处于双向受压.②弹塑性阶段:A点过后，变形速度明显加快，曲线偏向变形轴，在受压区，部分钢管的应力超过比例极限，混凝土的纵向压应力继续增加，达到B点时压区已产生紧箍力;在受拉区，钢管的应力超过比例极限的范围大幅度增加，达到B点时，钢管边缘屈服.③强化阶段:B点过后，弯矩缓慢增加，与变形轴成角度不大的斜线，在受压区，钢管最大纤维应力达到屈服点，并逐渐向内部扩展，混凝土在纵向压应力作用下，横向变形不断增加，紧箍力也逐渐增大;在受拉区，钢管边缘的屈服应力向内部发展.

图2 钢管混凝土构件M-φ曲线Fig.2 M-φ curve of CFST members

根据统一理论的研究结果，矩形钢管混凝土受弯构件M-φ曲线的数学表达式为

屈服点的弯矩和曲率取值为

极限点的弯矩和曲率取值为

将上述M-φ关系曲线在下列假定基础上，转化为程序需要的M-θ关系曲线:①单元内弯矩沿杆件为线性分布;②弹塑性变形集中于构件的两端区域;③反弯点位于构件的中点.

根据假定，取杆件长度一半作为计算转角的简化模型，以反弯点为坐标原点如图3所示.沿杆件方向，构件截面弯矩由0不断增加至Mu的过程中，其截面状态划分为两个区段:

图3 杆件M-φ分布图Fig.3 M-φ distribution curve of member

(1)当梁端A截面达到屈服弯矩My时，此时构件各截面状态均为第I区段，如图3(a)所示，梁端截面转角θby为第I区段的相对转角θI与反弯点处截面转角θoy之和，即

(2)当梁端A截面达到极限弯矩Mu时，构件曲率弯矩分布为第II区段，如图3(b)，对曲率进行分段积分可求得构件的相对转角，即为各阶段曲率所围成的面积，即

通过上述过程将钢管混凝土构件的M—φ关系转化为以M—θ表述的本构关系，并进一步转换为以M/My为横坐标、θ/θy为纵坐标的塑性铰本构关系的曲线形式.

2.2 钢管混凝土PMM铰

对于钢管混凝土构件PMM铰，除需计算纯弯时的弯矩-转角关系曲线外，还须计算构件的轴力—弯矩关系曲线.

钢管混凝土压弯构件轴力-弯矩关系曲线如图4所示，对于CD段和CAB段，分别近似采用直线和抛物线的函数描述.

图4 钢管混凝土轴力-弯矩相关曲线Fig.4 Relation curve between axial force and bend

钢管混凝土拉弯构件，按《矩形钢管混凝土结构技术规程》(CECS159:2004)规定选用.

3 有限元模型建立

3.1 试验资料

以文献［11］中钢管混凝土焊接桁梁试件及试验结果为依据，建立有限元分析模型.桁梁试件模型全长4 940 mm，计算跨径4 800 mm，高1 100 mm，节间距800 mm.弦管及斜腹管分别为100×100×4 mm、80×80×4 mm，竖腹管为60×40×3 mm，如图5所示.根据弦管内填混凝土的情况，将三个桁梁和节点分别编号，其中空钢管桁梁为A0，上弦填混凝土桁梁为A1，上下弦均填混凝土桁梁为A2.

图5 试验桁梁几何模型Fig.5 Physical model of test truss

3.2 Pushover模型

利用有限元程序Midas/Civil进行试验桁梁的Pushover分析，根据各试验桁梁的受力和变形特点，对其设置不同类型的塑性铰.对于A0桁梁弦杆设置钢管PMM铰，斜腹杆设置矩形钢管P较;对于A1桁梁下弦杆设置钢管PMM铰，上弦杆设置钢管混凝土PMM铰，斜腹杆设置钢管P铰;对于A2桁梁弦杆设置钢管混凝土PMM铰，斜腹杆设置钢管PMM铰.程序对钢管杆件PMM铰特性值，按《钢结构设计规范》(GB50017—2003)规定计算.钢管混凝土弦杆PMM铰特性值，按笔者方法计算;钢管混凝土弦杆的轴力-弯矩相关曲线，按笔者所给公式计算.

4 可行性验证分析

4.1 极限荷载

利用建立的杆系塑性铰模型，得到试验桁梁的极限荷载，并与实体模型和试验数值进行对比，表1为桁梁极限承载力的对比结果［12］.①就分析方法来看，实体模型和杆系塑性铰模型的数值结果较为接近，且与试验结果均有一定差异，在A1和A2桁梁中，两者极限荷载相差约10%，这是因为数值分析不受试验方法、材料缺陷、理论简化等因素的限制，但数值结果与试验结果的总体趋势较为吻合.②就桁梁极限荷载来看，A1和A2桁梁的极限荷载比A0桁梁均有一定程度的提高，且A2桁梁极限荷载的提高程度较大，这说明填充混凝土有效提高了桁梁的承载能力，且受拉弦杆中的混凝土贡献较大，其作用不可忽视.③就桁梁跨中挠度来看，A0和A1桁梁极限状态的跨中挠度较为接近，而A2桁梁跨中挠度相对较小，这是因为A0和A1桁梁中存在钢管节点，而A2桁梁中均为钢管混凝土节点，混凝土的存在极大的限制了节点变形.

表1 桁梁极限荷载数值对比Tab.1 Numerical comparison of truss ultimate load

4.2 失效模式

杆系塑性铰模型分析的优势在于，通过塑性铰的出现和发展，能够显示结构在极限破坏时的薄弱点.图6为各桁梁杆系塑性铰模型的失效模式，由图可知:A0桁梁破坏是由于受压弦杆节点失效而引起的，塑性铰出现在节点B和节点F，失效发生在钢管节点上;A1桁梁破坏是由于受拉弦杆节点失效而引起的，塑性铰出现在节点e和节点c，失效发生在钢管节点上;A2桁梁破坏是由于腹杆节点失效而引起的，塑性铰出现在节点c，失效发生在钢管混凝土节点上.3个桁梁极限破坏均发生在节点处，但失效节点的位置和类型不同，这说明管内填充的混凝土改变了节点的失效模式.

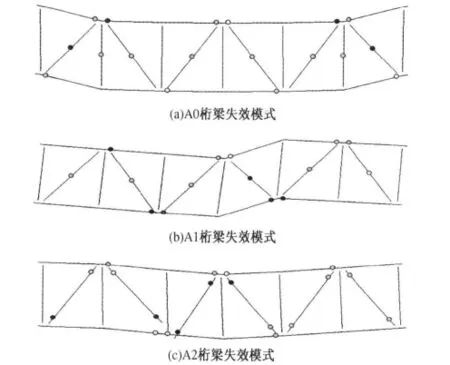
图6 桁梁塑性铰模型破坏模式Fig.6 Failure mode of plastic hinge model for trusses

A0和A1桁梁的失效模式与试验结果完全相同，但A2桁梁的失效模式稍有差异.试验中A2桁梁发生节点c弦杆表面冲剪破坏，而数值分析中A2桁梁发生节点c腹杆的有效宽度破坏，这是因为杆系塑性铰模型中无法具体体现有效宽度破坏和冲剪破坏的差别.

4.3 荷载—位移曲线

各个桁梁数值结果和试验结果的荷载位移曲线如图7所示.A0和A1桁梁数值结果和试验结果荷载位移曲线的发展规律十分符合，均呈现出较明显的弹性阶段、弹塑性阶段和下降段.A2桁梁由于受到试验方法的限制，没有测量出下降段，但其荷载位移曲线的发展趋势也十分相似.在弹性阶段，各桁梁数值结果和试验结果十分吻合.A0桁梁的刚度最小，因此荷载位移曲线的斜率最小;填充混凝土后A1和A2桁梁的刚度增大，因此其荷载位移曲线的斜率也增大.3个桁梁在弹性阶段极限荷载分别为300 kN、317 kN和342 kN，这说明填充混凝土可以提高桁梁在弹性阶段的承载能力.在弹塑性阶段，各桁梁数值结果和试验结果较为吻合.A0桁梁荷载位移曲线的斜率最小;而A1和A2桁梁的曲线斜率随刚度增大而增加.三个桁梁弹塑性阶段极限荷载为382 kN、416 kN和473 kN，说明填充混凝土可以提高桁梁在弹塑性阶段的承载力.就桁梁整体变形而言，各桁梁塑性发展过程有所不同.A0和A1桁梁的塑性发展过程较为相似，均是经历了较长的弹塑性阶段而达到极限状态;而A2桁梁的塑性发展过程则有所不同，弹塑性阶段较短且发生塑性变形时荷载仍然增加较快;这一规律也与试验结果相符，主要因为A0桁梁和A1桁梁的破坏由钢管节点控制，而钢管节点具有较强的塑性变形能力;A2桁梁的破坏由钢管混凝土节点控制，由于内填混凝土的约束效应，节点塑性变形能力较弱.由此可见，笔者建立的杆系塑性铰模型的分析结果与试验结果较为符合，将其应用于大型结构分析中是可信的.

图7 桁梁荷载位移曲线Fig.7 Load deflection curves for mid-span of trusses

5 结论

(1)根据钢管混凝土受弯构件统一理论的弯矩—曲率曲线，提出了钢管混凝土构件M铰屈服点和极限点确定的经验公式.

(2)对钢管混凝土构件弹塑性状态下截面弯矩—转角关系进行推导，给出了适合于Pushover分析的钢管混凝土M铰和PMM铰特性值的计算方法.

(3)Pushover分析与试验结果的对比表明，笔者提出的钢管混凝土构件塑性铰特性值的确定方法是合理可行的，对钢管混凝土桁梁极限承载力的分析是可信的，为大型钢混组合桁梁梁桥在弹塑性阶段静、动力性能提供了有效的理论基础和研究手段.

［1］黄文金，陈宝春.钢管混凝土桁梁受弯试验研究［J］.建筑科学与工程学报，2006，26(1):29-33.

［2］吝红育，刘永健，任翔.矩形钢管混凝土桁架非线性有限元分析.郑州大学学报:工学版，2011，32(5):15-19.

［3］李运喜.受压弦杆填充混凝土的矩形钢管桁梁静力性能研究［D］.西安:长安大学公路学院，2008.

［4］刘君平.主管填混凝土矩形钢管桁架受力机理及设计方法研究［D］.西安:长安大学公路学院，2009.

［5］和兆建.矩形钢管混凝土桁架结构在连续刚构桥中的应用研究［D］.重庆:重庆交通大学土木建筑学院，2011.

［6］伍忠林.矩形钢管混凝土桁架拱桥及其静力性能分析［D］.西安:长安大学公路学院，2011.

［7］ATC—40.Seismic evaluation and retrofit of concrete buildings［R］.Redwood City，California:Applied Technology Council，1996.

［8］FEMA-356 Prestandard and commentary for the seismic rehabilitation of buildings［S］.Washington D.C，2000.

［9］北京迈达斯技术有限公司.MIADS/Civil分析与设计原理［DB/CD］.北京:北京迈达斯技术有限公司，2010.

［10］韩林海.钢管混凝土结构—理论与实践［M］.北京:科学出版社，2000.

［11］刘永健，刘君平，杨根杰.主管内填充混凝土矩形钢管桁梁受力性能试验研究［J］.建筑结构学报，2009，30(6):107-112.

［12］吝红育.部分填充混凝土矩形钢管桁架力学性能及桥梁应用研究［D］.西安:长安大学公路学院，2011.