字符串模式匹配算法的研究及改进

毕智超

（陕西职业技术学院,陕西西安,710100)

0 引言

在计算机信息科学领域里面，模式匹配是一个重要的研究课题。在拼写检查、基于字典的语言翻译、万维网搜索引擎、计算机病毒特征码匹配、数据压缩、以及DNA序列匹配等应用中，都需要进行模式匹配。字符串的模式匹配问题描述如下：设T和P是两个给定的串，在串T中找等于P的子串的过程称为模式匹配，其中，T称为主串，P称为模式。如果找到，称为匹配成功，否则称为匹配失败。

模式匹配问题的特点：

（1）算法的一次执行时间不容忽视：问题规模通常很大，常常需要在大量信息中进行匹配；

（2）算法改进所取得的积累效益不容忽视：模式匹配操作经常被调用，执行频率高。

如何改进模式匹配算法、提高模式匹配效率, 是本文研究的一个关键问题。

1 朴素的模式匹配BF算法

BF算法是一种简单直观的模式匹配算法，其基本思想是：从主串T的第一字符开始和模式P的第一个字符进行比较，若相等，则继续比较两者的后续字符；否则，从主串T的第二个字符开始和模式P的第一个字符进行比较。重复上述过程，若P中的字符全部比较完毕，则说明匹配成功，返回主串T在本趟比较中的起始位置；否则匹配失败，返回0。

例如 ：主串 T=t0t1t2…tm-1…tn-1，模式 P= p0p1p2…pm-1。如果t0=p0，t1=p1，t2=p2，…tm-1=pm-1，则匹配成功，返回模式串第 0个字符p0在主串中匹配的位置；如果在其中某个位置i：ti≠pi，比较不等，这时可将模式串P右移一位，用P中字符从头开始与T中字符依次比较。如此反复执行，直到出现以下两种情况之一，就可以结束算法：一种情况是执行到某一趟，模式串的所有字符都与目标串对应字符相等，则匹配成功；另一种情况是P已经移到最后可能与T比较的位置，但不是每一个字符都能与T匹配，这是匹配失败的情形，函数将返回0。

这个算法是一种带回溯的算法。一旦比较不等，就将模式P右移一位，从p0开始在进行比较。若设目标T的长度为n，模式P的长度为m，在最坏情况下，最多比较n-m+1趟，每趟比较都在最后才出现不等，要做m次比较，总比较次数达到（n-m+1）*m。在多数场合下m远远小于n，因此，算法的时间复杂度为O(n*m)。

2 模式匹配的KMP算法

分析以上算法可知，BF算法是一种带回溯的匹配算法，也正是回溯使得BF算法效率低下。事实上，这些回溯并不一定是必要的。

例如 ：主串 T=t0t1…tn-1，模式 P= p0p1…pm-1。用前面介绍的BF算法做第s趟比较时，从目标T的第s个位置ts与模式P的第0个位置p0开始进行比较，直到在目标T第s+j位置ts+j“失配”。这时，应有 tsts+1ts+2…ts+j-1= p0p1p2…pj-1(1), 按 BF 算法，下一趟应从目标T的第s+1个位置起用ts+1与模式P中p0对齐，重新开始匹配比较。如果在模式P中，p0p1…pj-2≠p1p2…pj-1（2），则第s+1趟不用进行比较，就能断定它必然“失配”。因为由（1）式和（2）式可知：p0p1…pj-2≠ts+1ts+2…ts+j-1（= p1p2…pj-1）既然如此，第s+1趟可以不做。依次类推，直到对于某一个值k，使得 ：p0p1…pk+1≠ pj-k-2pj-k-1…pj-1且 p0p1…pk= pj-k-1pj-k…pj-1才有 p0p1…pk= ts+j-k-1ts+j-k…ts+j-1(=pj-k-1pj-k…pj-1),这样，我们可以把在第s趟比较“失配”时的模式P从当前位置直接向右“滑动”j-k-1位。这时，因为目标T中ts+j之前已经与模式P中pj之前的字符匹配了，故而可以直接从T中的ts+j与模式中的pk+1开始，继续向下进行匹配比较。

在这个算法中，目标T在第s趟比较失配时，扫描指针s不必回溯。算法下一趟继续从此处开始向下进行匹配比较；而在模式P中，扫描指针p应退回到pk+1位置。

关于k的确定方法，可以用一个next特征函数来确定：当模式P中第j个字符与目标T中相应字符失配时，模式P中应该由哪个字符（设为第k+1个）与目标中刚失配的字符重新继续进行比较。特征函数next定义如下：

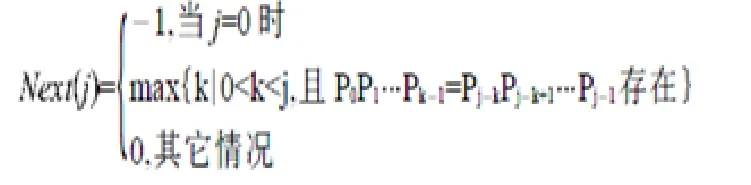
设模式串长为m，则求next的算法时间复杂度是O(m)。若主串长为n，KMP算法的时间复杂度是O(n)；如果包括求next(j)的时间，KMP算法的时间复杂度是O(n+m)。

3 改进的模式匹配算法

串模式匹配算法待解决关键问题是：模式串在主串某个位置比较失败时，如何使模式串向右移动最佳距离，尽量多的跳过不必要比较的字符，减少匹配的次数。通过上述匹配算法的分析研究，可以看出KMP算法避免了BF算法频繁回溯，提高了模式匹配的工作效率，但是我们对于模式匹配算法还可以进一步改进，最大限度的减少匹配的次数。改进后的算法简单实用，便于理解。

改进算法的精髓是对模式串移动距离的确定。同理设主串T=t0t1…tn-1，模式 P= p0p1…pm-1。我们做匹配比较时，设目标 T 的第i个位置ti与模式P的第0个位置p0开始进行比较。在比较过程中失配于 pj处，即 titi+1ti+2…ti+j-1= p0p1p2…pj-1，且 ti+-j≠pj。首先定义一个特征函数S来确定主串中出现的字符x（x的值为当前字符）在模式P中的位置。此算法还要在模式P中补充一个字符pm，该字符的位置紧随pm-1，取值可任意，其目的一是方便对特征函数S（x）的定义；二是x能取到ti+m的值。这样模式P= p0p1…pm-1pm。

特征函数S（x）定义如下：

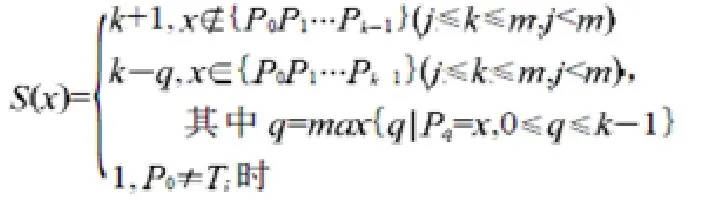
其中，x在目标T中取值，取失配位置j和其后的字符即x=ti+k，j≤k≤m，且x取值位置的变化可产生前面模式串的子串p0p1…pk-1长度的变化。特征函数S（x）的作用是求失配时模式串P向右滑动的合理距离，这样就可以减少匹配次数。

此算法如果模式P字符数m较大，此时在逐一的计算求滑动距离，那么算法收益明显降低。其实可采用目标T中的三个位置的字符来计算，分别为ti+j、ti+j+1和ti+m。之所以让ti+j+1和ti+m参与进来决定模式P的滑动距离其目的有二：一是减少函数S的运算次数；二是如果前面发生失配，那么模式势必需要向右滑动。假如S（ti+j+1）和S（ti+m）的取值有一方属于函数S的第二种情况，最终移动距离的确定属于该方，这时ti+j+1和ti+m对于移动距离属于该方的必然会有模式移动的距离与模式中和它相同的字符对齐。假如这两位置上的字符有一方不属于模式串时，最终移动距离的确定属于该方，这时能够获得最大的滑动距离。所以我们之需要考虑它们参与所产生的移动距离即可。此算法最终移动距离的确定是通过计算 S（ti+j）、S（ti+j+1）和 S（ti+m）并取其最大值。

下面通过一个实例来说明滑动距离的求解。

例 ：T=“thefollowsamaselomesample”,P=“sample”。第 一趟比较：i=0，j=0，0≤k≤6，S(x=t0=t)=1(因为p0≠ti，取函数S的第三种情况)；S(x=t1=h)=2（k=1，h∉ {p0}，取函数S的第一种情况）；但 S(x=t6=l)=2（k=6，l∈ {p0p1p2p3p4p5}且q=4，取函数S的第二种情况）。模式移动位移为2。

第二趟比较：i=2，j=0，0≤ k≤ 6，S(x=t2=e)=1；S(x=t3=f)=2；S(x=t8=w)=7。模式移动位移为7。

第三趟比较：i=9，j=3，3≤ k≤ 6，S(x=t12=a)=2；S(x=t13=s)=4；S(x=t15=l)=2。模式移动位移为4。

第四趟比较：i=13，j=1，1≤ k≤ 6，S(x=t14=e)=2；S(x=t15=l)=3；S(x=t19=s)=6。模式移动位移为6。

第五趟比较：i=19，匹配成功。

匹配过程如下图所示

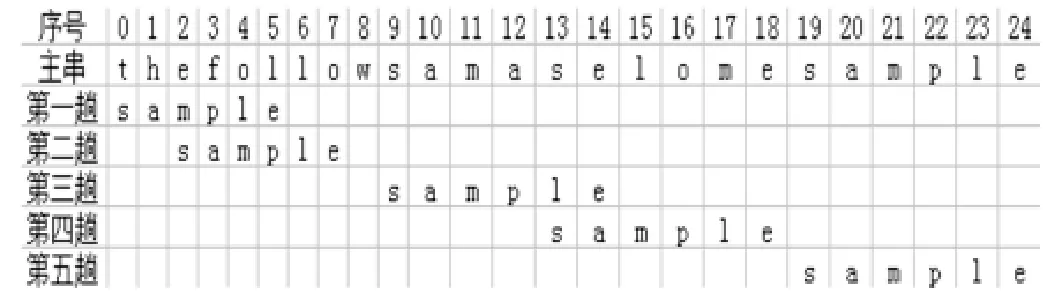
图1 模式匹配过程

笔者通过实验论证，对于上述实例用改进后的算法需要进行5趟共12次字符比较；而KMP算法需要18趟共27次字符比较。如果问题规模很大时，此算法更能体现出它的高效求解。

4 结束语

字符串模式匹配技术在当今已经成为解决计算机科学中的关键技术之一。本文改进后的算法能够很大程度上提高匹配检测的效率。如何能更好的应用此算法，是我们今后研究的工作重点。

[1]李洋,王康,谢萍.模式匹配改进算法[J].计算机应用研究,2004,21(4):58-59.

[2]程伟,刘玉军,卢泽新.最佳比较序字符串匹配算法研究和应用[J].计算机工程与设计2004,25(9):1430-1432.

[3]殷人昆.数据结构(用面向对象方法与C++语言描述)[M].北京:清华大学出版社,2007.