面向动态特性快速求解的铣刀等效建模方法
张 俊,黄保华,赵万华,刘春时,卢秉恒
(1.西安交通大学机械制造系统工程国家重点实验室,陕西 西安 710049;2.沈阳机床(集团)有限责任公司高档数控机床国家重点实验室,辽宁 沈阳 110141)
引 言
高速/超高速加工由于具有效率高、加工精度好等优点现已逐步应用于航空航天、发电设备等行业的结构件加工上,然而影响其有效高速加工的一个主要因素就是颤振。在实际工程中为避免颤振发生的一个有效方法是借助于该机床的切削稳定性极限图(俗称“叶瓣图”)来选择合适的切削参数[1~3]。采用锤击法得到叶瓣图是一种常用的方法,但是该方法费时且适用性差,当机床结构发生变化时,其叶瓣图也会发生变化,需重复使用锤击法测试,因此不适合如今生产中频繁更换刀具和刀柄的各种加工中心。
2000年Schmitz等学者提出了一种计算刀尖点频响函数的快速求解方法[4],该方法通过将机床整机分成若干个子结构,如刀具、刀柄、主轴以及机床其他部件,分别计算或测试出各子结构的频响函数,再耦合成整机的频响特性,从而得到整机的切削稳定性极限图。对于其中的刀具结构,如常用的整体立铣刀,由于刀齿部分较为复杂,不利于频响函数的快速计算,通常将其等效成均匀直径梁。Kops和Vo利用刀齿柔度相等(也就是刚度相等)的原则计算出了其等效梁模型的直径[5],对于所测试的2齿和4齿立铣刀,等效模型和实际模型的受力变形误差大约在2.25%。Zhang等则在当量直径的计算上采用了刀齿质量相等的方法[6],从最终预测的整机频响函数与实测结果来看,拟合精度较好。而其他绝大部分文献在计算刀具频响时[7~9],均不区分刀杆和刀齿,统一将其等效为一均匀直径梁,取铣刀最外端的包络圆直径作为等效直径,这一简化大大方便了频响计算,但均未提及其带来的影响。
刀齿等效模型的准确建立是影响整机频响特性准确预测的一个重要方面,从目前发表的文献来看,还未有学者对此问题做一个系统的研究。因此本文从刀具结构出发,分别借助于等质量、等截面积、等刚度的原则,比较这3种方法在刀具等效模型建立上的优缺点,为今后模型的合理建立提供依据。
1 铣刀等效模型的建立
以整体立铣刀为研究对象,图1(a)为某型号立铣刀,采用激光扫描测量系统(型号:Faro P12-7)对其进行三维轮廓扫描,再根据扫描的点云数据进行实体重构得到其三维模型,如图1(b)所示。为了快速计算铣刀的频响特性,将其刀齿部分等效为均匀直径梁,如图2所示。
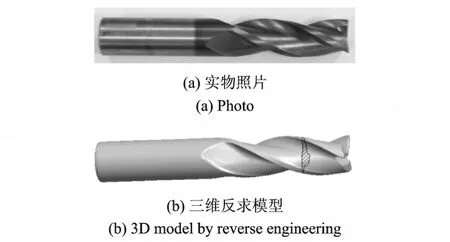
图1 某型号整体立铣刀Fig.1 Endmill

图2 整体立铣刀的等效模型Fig.2 Equivalent model of endmill
1.1 等质量法(EqM)
根据刀齿部分质量与等效后均匀直径梁质量相等的原则,计算得出等效模型的直径dm,如下式所示
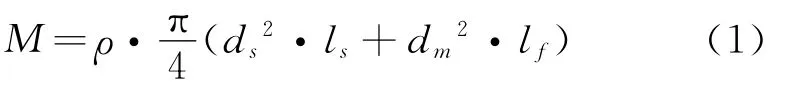
式中M为铣刀总质量,ρ为刀具材料密度,且ρ=14 605kg/m3,ds和ls分别为刀杆直径和长度,lf为刀齿长度。
1.2 等截面积法(EqA)
整体立铣刀的刀齿为螺旋形,其截面面积均相等。因此以任一截面为基准,根据面积相等的原则,将刀齿截面等效为圆截面,利用下式计算出等效模型的直径da

式中Af为刀齿的截面积。如果不考虑刀齿前端和刀齿向刀杆过渡的局部特征,则等质量法计算所得的dm与等截面积法算出的da是相同的。
1.3 等刚度法(EqK)
将实际状况下的刀齿看成一悬臂梁,则其刚度可通过下式计算

对同一长度梁而言,可以用截面的惯性矩来表征整个梁的刚度,因此该方法也称为“等惯性矩”法。根据刀齿结构等效前后的刚度相等原则,根据下式计算出等效模型的当量直径dk

式中k和I分别为刀齿的刚度和二阶惯性矩,E为弹性模量,且E=560GPa。
以图3中的4把整体立铣刀为研究对象,其切削齿t分别为2,3,4和6。应用以上3种方法对其等效处理,铣刀的原始结构尺寸(刀齿长度lf,刀杆长度ls,刀齿和刀杆直径d)和等效后的当量直径(等质量法dm,等截面积法da,等刚度法dk)如表1所示。由表1可知,无论是哪把铣刀,等刚度法得到的等效直径都为最大。

图3 4种整体立铣刀结构Fig.3 Four endmills used for analysis

表1 4种铣刀的结构参数与3种等效直径Tab.1 Geometry and equivalent diameters of four endmills
2 铣刀等效模型的频响特性
2.1 频响函数计算
等效后的刀杆和刀齿均为均匀直径梁,考虑到其长径比不够大,数值计算时采用考虑截面效应和剪切效应的Timoshenko梁模型[10],该模型比不考虑以上两效应的Euler-Bernoulli梁更为精确,其微分方程为
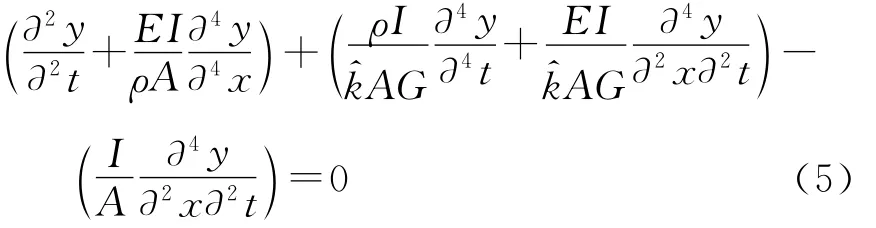
式中为梁截面的形状因子[11],G为剪切模量。
两端均自由的梁有4个自由度(两个转角θ和两个位移x),共分成n个单元进行求解,每个单元通过质量M矩阵和刚度K矩阵建立起力f(力矩m)和位移(转角)之间的关系,如式(6)所示。
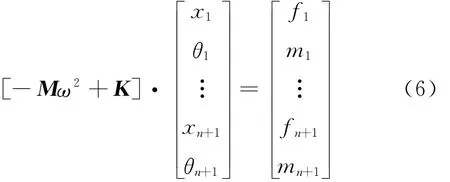
式中f和m分别为施加在梁单元两端的力和力矩。因此,单元的频响函数矩阵Rij可以写成
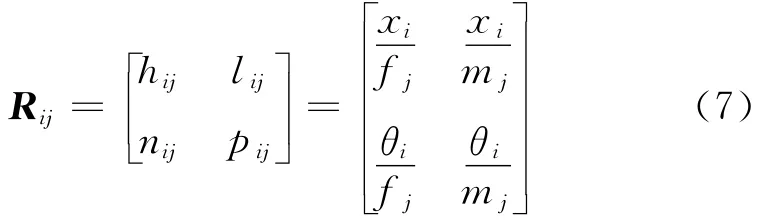
2.2 刀齿和刀杆的频响函数耦合
通过Timoshenko梁模型计算出刀齿和刀杆的频响函数后,再根据子结构法对其进行刚性耦合,得到铣刀两端自由状态下的频响函数[12],如下式所示
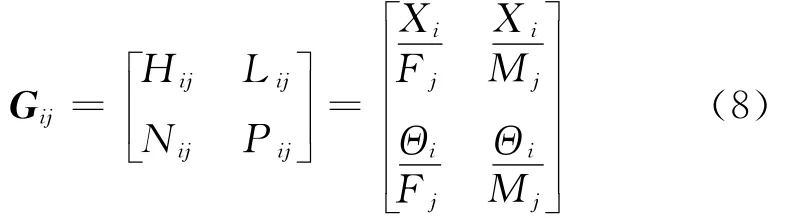
3 铣刀的频响特性测试
将整体立铣刀的两端用弹性皮筋悬挂起,以模拟其自由状态。在铣刀刀尖处布置一个PCB微型加速度传感器(型号:352C23),传感器采用蜂蜡粘结。考虑到试件的结构尺寸,选用了PCB小型力锤(型号:M352C65)。测振系统为LMS Test.Lab(型号:SCM05)。通过数据采集与分析系统在计算机中显示出其频率响应函数曲线,每次均取10次有效锤击(相干系数大于0.8)的统计平均值作为最后分析结果。
为验证实验装置和测试方法的准确性,特以一均匀直径钢棒(直径27.8mm,长度224.40mm)为验证对象(图4),原点响应的测试值和理论计算值如图5所示,二者吻合很好,说明测试系统和测试方法均为可行。
按照上述方法对图3中的4把整体立铣刀分别进行测试(图6),就可以获得铣刀刀尖点的原点响应。

图4 验证用的测试钢棒、力锤和传感器Fig.4 Tested cylinder,hammer and sensor
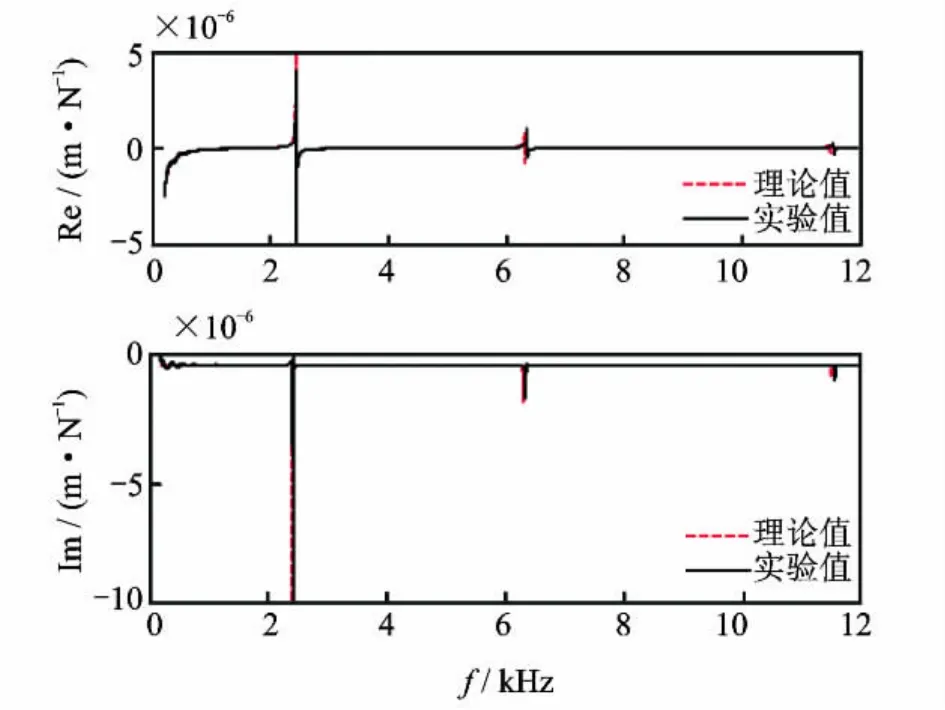
图5 钢棒原点响应的理论值和测试值Fig.5 Theorical and measured direct receptance of tested cylinder

图6 铣刀的频响特性测试Fig.6 Impact testing for endmill′s FRF
4 结果分析与讨论
4.1 频响特性
图7给出了铣刀B和D在8 000Hz范围内的频响函数曲线(实部Re和虚部Im),包括锤击法的实验测试(Exp)和3种等效模型方法(EqM,EqA和EqK)的计算结果。在非固有频率区域,等效模型预测值与实验测试结果吻合很好;在固有频率附近,不同的等效方法表现出不同的吻合程度,二者的详细误差分析见下节。
采用等效模型和子结构方法计算铣刀的频响函数曲线可以在很短的时间内完成。然而,如果通过采用构建铣刀三维模型,再对其进行有限元谐响应分析得到其频响函数曲线,则需要数百倍的时间。因此,等效模型的合理建立可以为后续整机稳定性的快速预测奠定基础。
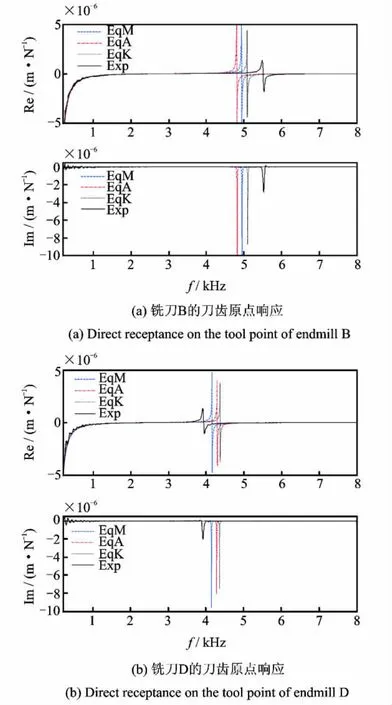
图7 铣刀的频率响应曲线Fig.7 Endmill′s FRF
4.2 固有频率
由于铣刀在自由状态下前6阶固有频率均为零,所以本文为便于表述,将其不为零的第7阶作为第1阶。表2~4分别列出了4把立铣刀前3阶固有频率的实验测试值和等效模型计算值及其绝对误差。由3种等效模型的计算值误差率可以看出,对于铣刀A,B和C,即2齿、3齿和4齿的铣刀而言,等刚度法的误差最小,具有最好的预测精度。而对于具有6齿的铣刀D而言,等质量法的预测精度要高于等截面积法和等刚度法。
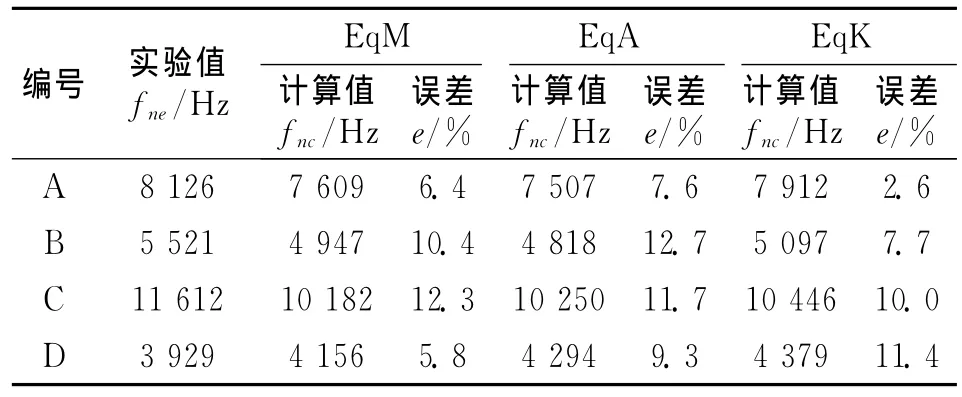
表2 第1阶固有频率Tab.2 The first natural frequency
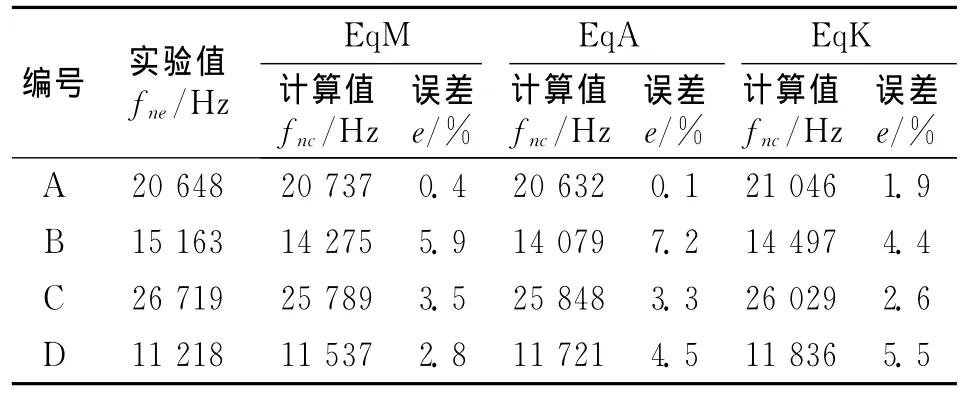
表3 第2阶固有频率Tab.3 The second natural frequency
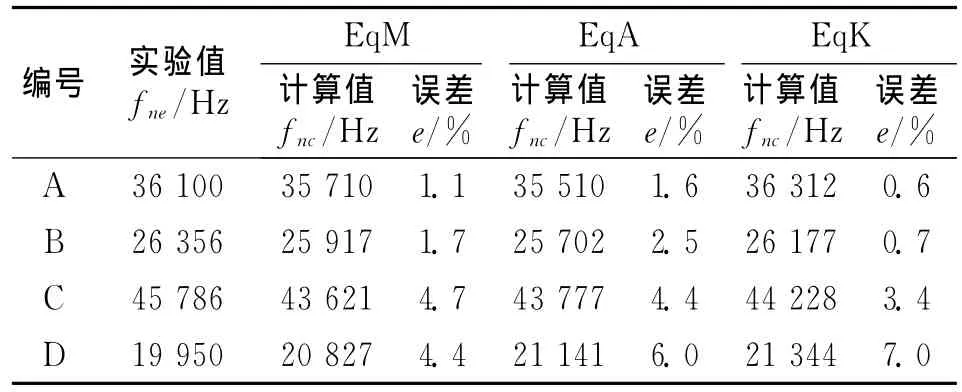
表4 第3阶固有频率Tab.4 The third natural frequency
4.3 讨论
对于4把铣刀,采用等刚度法得到的等效模型(或者说等效直径),再计算其质量,并将等效模型的质量与铣刀的原始质量对比,如表5所示,不难发现铣刀A,B和C的误差比较接近,在3%左右;而铣刀D的误差达到了5.6%,明显大于前三者。因而对于铣刀D而言,采用等刚度法达到的精度显然要低于铣刀A,B和C。

表5 采用等刚度法后的等效模型质量及误差Tab.5 The mass of equivalent model and its error by using equal stiffness method
然而,从以上的分析结果并不能下结论说等刚度法适合用于疏齿铣刀(如铣刀A,B和C),而等质量法适合用于密齿铣刀(如铣刀D)。实际上3种方法的适用范围会随铣刀结构参数而改变的。借助于有限元方法对整体立铣刀进行了单因素的影响分析,分析之前通过以上的实验测试结果验证了有限元计算的准确性。图8分别给出了不同刀齿截面惯性矩(体现为不同的齿数t)、螺旋角β、刀齿长度占铣刀总长比例κ=lf/l,以及刀具长径比γ=l/d参数下,3种等效方法相对误差er的变化曲线(从相对误差可以看出该参数的具体数值下,3种等效方法所引起的是正偏差还是负偏差,因为多因素综合作用下,各因素所带来的误差可能会相互抵消),从变化的误差值可知这4个因素都将影响3种等效模型的适应范围,其中β和κ的影响要大于其他两因素。
各参数间引起的相对误差与总误差之间可采用多元线性关系下式表示
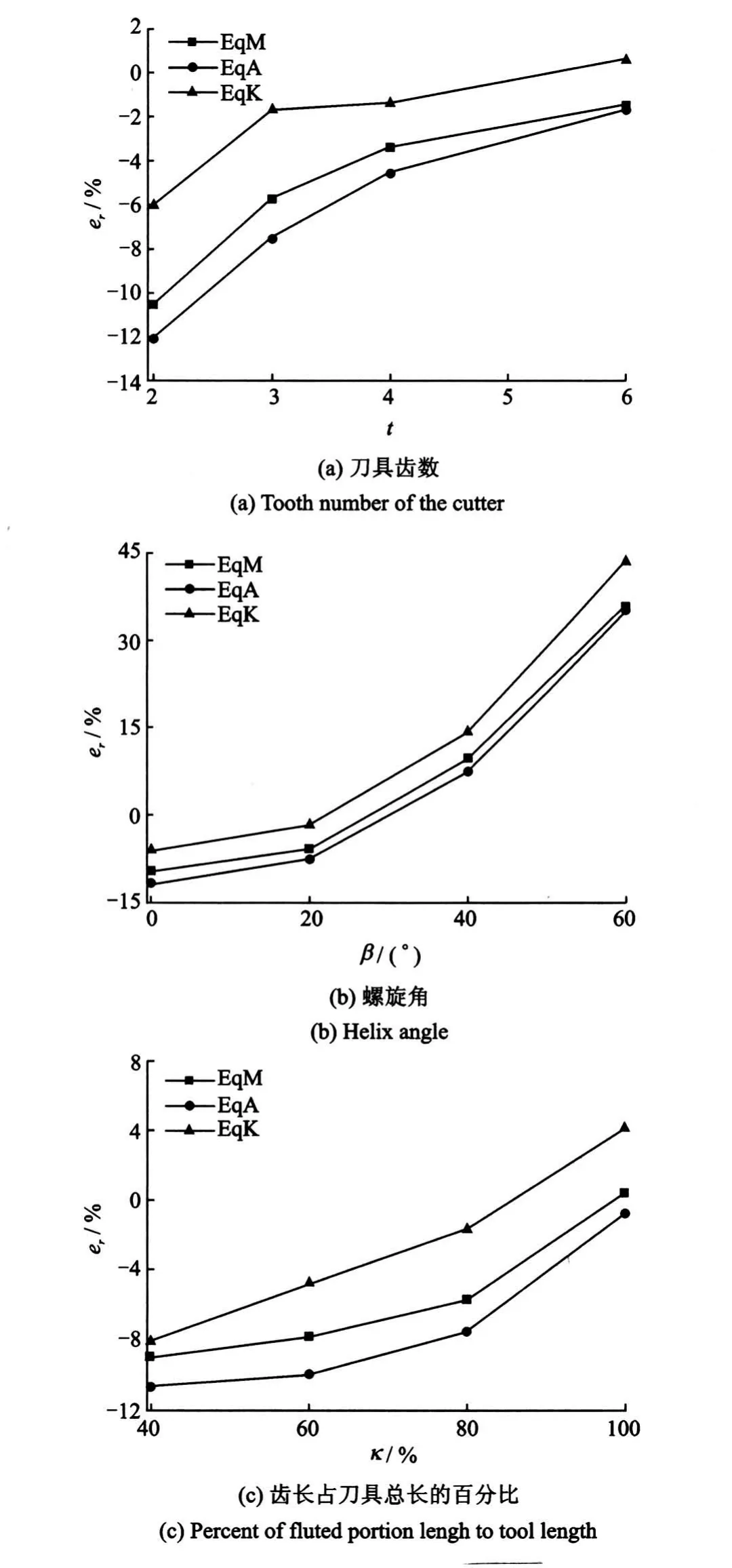
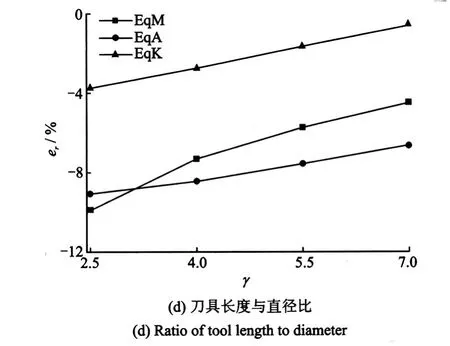
图8 4因素引起的3种等效方法的相对误差Fig.8 Relative error of three equivlent model by four factors
式中et为总相对误差,αi为因素引起的相对误差的影响系数。假设忽略影响系数α,则可得到et与eri之间的简单代数关系。将上文的4把铣刀(A,B,C和D)的参数分别参照图8的分析结果,得到每参数的相对误差值E,综合后得到总误差,结果如表6所示。由表6中数据同样可以看出对于铣刀A,B和C而言,等刚度法预测精度最高;对于铣刀D,等质量法预测精度更好。这与前文4.2的分析结果很吻合,但表6中数据不能代表其实际误差值,因为未考虑各因素的影响程度,即影响系数α。
5 结 论
(1)基于机床整机稳定性快速预测的思想,分析了铣刀频响函数快速求解的3种等效模型方法(等质量法、等截面积法、等刚度法)的优缺点和各自的适应性。
(2)可将铣刀分成刀杆和刀齿两部分,分别求解其频响函数,再通过子结构方法将其耦合为铣刀整体的频响函数,该方法有效克服了采用有限元方法计算整体铣刀频响函数速度慢的缺点。
(3)分析了刀齿截面惯性矩、刀齿螺旋角、刀齿长度占总长百分比和铣刀长度与直径比值等4个因素对3种等效方法所引起的相对误差变化规律,并根据此规律解释了铣刀A,B,C采用等刚度法计算精度最高,而铣刀D采用等质量法计算精度最高的原因。
[1] Gradisek J,Kalveram M,Insperger T,et al.On stability prediction for milling[J].International Journal of Machine Tools and Manufacture,2005,45:769—781.
[2] Solis E,Peres C R,Jime J E,et al.A new analyticalexperimental method for the identification of stability lobes in high-speed milling[J].International Journal of Machine Tools and Manufacture,2004,44:1 591—1 597.
[3] 赵宏伟,王晓军,于骏一.机床再生型切削颤振系统稳定性极限预测[J].西南交通大学学报,2003,38(5):547—552.
Zhao Hong-wei,Wang Xiao-jun,Yu Jun-yi.Prediction of stability limits for regenerative chatter system of machine tools[J].Journal of Southwest Jiaotong University,2003,38(5):547—552.
[4] Schmitz T,Donaldson R.Predicting high-speed ma-chining dynamics by substructure analysis[J].Annals of the CIRP,2000,49(1):303—308.
[5] Kops L,Vo D.Determination of the equivalent diameter of an end mill based on its compliance[J].Annals of the CIRP,1990,39(1):93—96.
[6] Zhang J,Schmitz T,Zhao W H,et al.Receptance coupling for tool point dynamics prediction on machine tools[J].Chinese Journal of Mechanical Engineering,2011,24(3):340—345.
[7] Park S S,Altintas Y,Movahhedy M.Receptance coupling for end mills [J].International Journal of Machine Tools & Manufacture,2003,43(9):889—896.
[8] Ert¨urk A,¨Ozg¨uven H N,Budak E.Analytical modeling of spindle-tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF[J].International Journal of Machine Tools & Manufacture,2006,46(15):1 901—1 912.
[9] Filiz S,Cheng C H,Powell K,et al.An improved tool-holder model for RCSA tool-point frequency response prediction[J].Precision Engineering,2009,33(1):26—36.
[10]Weaver W,Timoshenko S P,Young D H.Vibration Problems in Engineering[M].5th ed.New York:John Wiley and Sons,1990.
[11]Hutchinson J R.Shear coefficients for Timoshenko beam theory[J].Journal of Applied Mechanics,2001,68(1):87—92.
[12]Schmitz T,Smith K.Machining Dynamics:Frequency Response to Improved Productivity[M].New York:Springer,2009.

