基于改进离散粒子群的蜂窝网络信道分配

冯志强，贾振红，许国军

（1.新疆大学 信息科学与工程学院，新疆 乌鲁木齐830046；2.中国移动通信集团新疆有限公司，新疆乌鲁木齐830063）

0 引 言

在蜂窝移动通信网络中，随着用户的急剧增长，可用的频率资源变得极为稀少，为了提高频谱的利用率必须要引入较优的频率分配策略。频率分配，又称为信道分配问题 （channel assignment problem），属于组合优化中的 NP（nondeterministic polynomial）完备问题。针对信道分配问题国内外提出的优化算法有：蚁群算法、神经网络算法、模拟退火算法、遗传算法和进化策略等［1－7］，这些优化算法已经被证明可以用来解决信道分配问题，但这些算法在搜索最优解的过程中，依然存在算法复杂、收敛率较低、容易陷入局部最优解等缺点。粒子群算法是新兴的群智能算法，参数简单和收敛迅速使其得到了广泛的关注和应用。粒子群算法极易早熟，如何增加算法的全局搜索能力，已经成为研究的热点。针对上述问题，本文提出了一种改进的离散粒子群优化算法 （IDPSO）。该算法根据文化算法的思想设计了最优渐进式变异算子，使一个最优粒子向着全局最优解变异，其它最优粒子进行随机变异，增加了粒子的多样性，提高了算法的收敛率。又因采用了最小间距编码，压缩了求解空间，使得算法的收敛速度得到提高。

1 信道分配问题模型

在蜂窝小区制中，CAP要考虑的电磁兼容 （EMC）限制有：①同信道约束 （CCC）；②邻信道约束 （ACC）；③同小区约束 （CSC）［8］。数学上建立的信道分配问题模型详见文献 ［8］，代价函数为

其中F是一个n×m的矩阵，表示一种信道分配方案，若f（i，a）＝1，表示信道a分配给小区i，若f （i，a）＝0，表示信道a未分配给任何小区。当所有的限制都满足时，代价函数C（F）＝0，表示找到了一种最优的分配方案。CAP问题的目的就是找到一个解F使得C （P）＝0。

2 离散粒子群算法

粒子群优化算法是一种新兴的智能优化算法，算法结构简单，求解速度快。离散粒子群算法在粒子群算法的基础上被提出，用来解决工程中的离散问题。离散粒子群算法根据如下公式更新粒子的速度和位置［9］

其中c1、c2和c3是取值在0到1之间的常数，vi（t）表示t时刻粒子i的速度，xi（t）表示t时刻粒子i的位置，pi（t）表示t时刻粒子i的局部最优位置，pg（t）表示t时刻粒子i的全局最优位置。

3 改进的离散粒子群算法

3.1 个体编码

本文采用了文献 ［10］的最小间距编码方案，编码前的二进制串长度n，编码后二进制串的长度是：n－ （d－1）（dmin－1）。n表示可用的信道数，d表示小区的信道需求，dmin表示同小区的最小信道间隔。对于固定的信道数，小区需求d越大，编码后的长度越小，解空间的压缩比越大。编码后的粒子满足CSC约束条件，代价函数可以简化为［10］

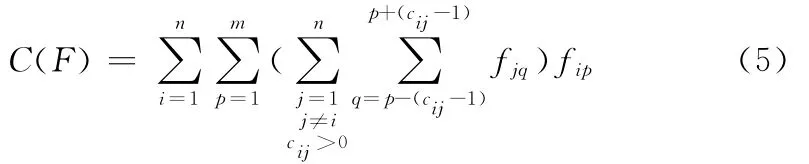
在工程实际应用中，在满足用户需求的情况下，必须使已用频点数越小越好。为了求得最小频点数，采用如下代价函数

其中α和 （是取值介于0和1之间的系数，M表示当前分配方案中所需的频点数。当O （F）求得最小值时，C （F）和M也必然求得最小值。

3.2 粒子的位置和速度

粒子的位置P表示为分配给一个小区的频率组成的m维向量，m表示小区的频率需求。P的第i维表示小区的第i个需求所分配的频率号，其公式表示如下

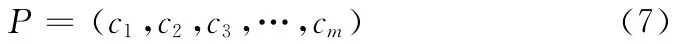
其中ci∈ ｛1，2，3，…，C｝，C表示最大的频率数目，m表示小区的频率需求。

本文使用交换算子 （i，j）表示小区的当前信道i和即将要切换到的信道j，m个交换算子就构成了粒子的速度

如果令V1＝ （i1，i2，i3，…，im），V2＝ （j1，j2，j3，…，jm），V1就是粒子的当前位置，V2就是粒子要移动到的目的位置。粒子的位置减法运算公式［9］变为：V＝V1ΘV2，V1＝P1，V2＝P2。因此，可以由粒子位置P1和P2直接得到粒子的速度。P1和P2中可能存在相同的信道，直接由P1和P2得到的速度交换算子，使粒子在移动后可能就不再满足小区的信道需求了。因此，将得到的V2限定如下

这样就由粒子位置P1和P2形成了粒子速度V，粒子按速度V移动后仍满足小区的频点需求。式 （3）和式 （4）中的其他运算规则详见文献 ［9］。

3.3 最优渐进式变异算子

在粒子的位置更新过程中，随着粒子向最优粒子的靠拢，会出现多个最优粒子，从而降低了粒子的多样性，使算法陷入局部最优解而无法获得全局最优解。为了提高算法的局部搜索能力，保证算法的收敛速度和收敛率，本文设计了最优渐进式变异算子：①统计当前粒子群中的最优粒子个数，并从最优粒子中随机选择一个做为全局最优粒子。②对这个全局最优粒子，将小区i的第n个已分配信道随机替换为未分配的信道 （i表示小区号，n表示小区i中的第n个需求）。③计算已替换后粒子的适应度，如果该适应度优于替换前粒子的适应度，则用变异后的粒子替代之前的粒子，否则，恢复已变异的元素。④反复执行②和③直到所有小区的所有信道需求元素都经过替换。⑤当所有的需求信道都替换后仍无较优粒子出现，则保留这个最优粒子，对剩下的最优粒子进行随机变异。这种变异方式使最优粒子总是朝着问题的最优解方向变异，防止了退化的出现，减少了最优粒子的个数，提高了粒子的多样性，使粒子跳出局部最优值，增强了算法的全局搜索能力。最优渐进式变异算子可以表示为

式中：F——最优渐进式变异操作，fi——粒子i的适应度，fb——最优粒子的适应度。粒子按式 （3）更新位置后，按式 （10）更新位置。最优渐进式变异算子是以增加算法的运算时间来提高进化过程中的种群多样性的，从而使算法的收敛率得到提高。

3.4 变异概率的确定

粒子位置的不同而表现出的多样性称为种群多样性，它是评价粒子群搜索可能解的重要尺度［11］。当粒子的多样性降低时，粒子开始出现聚集现象。只有粒子出现聚集的时候才需要对粒子进行变异，而且每个粒子的变异概率应该是不一样的。本文引入文献 ［11］中的方法来判断粒子的聚集程度。定义

式中：fi——第i个粒子的适应度，favg——全体粒子的平均适应度。从式 （11）可以看出：α2反映了粒子的聚集程度，其值越小，说明粒子的聚集程度越高，可以将这个值作为变异发生的条件。当α2＝0时算法要么陷入局部最优，要么已经找到全局最优。

为了保证进化的平稳性，在粒子没有聚集或聚集较小的时候，应以较小的概率对粒子进行变异甚至不变异，而粒子聚集比较严重时，应该以较大的概率对粒子进行变异。因此，在迭代的过程中，变异概率应该是动态变化的，不同粒子的变异概率也是不同的。本文修改正态分布函数为变异概率公式

当个体适应度接近平均适应度时取得较大的变异概率，相反，变异概率会很小。变异概率在0和1之间，只有当粒子聚集严重时才会以概率1进行变异。综上，当α2＜C时，按照式 （12）的变异概率执行最优渐进式变异算子。

3.5 算法复杂度分析

粒子群算法的时间复杂度主要依赖于迭代次数t、粒子维数m和粒子的适应度计算，这里认为粒子数是一个常数。在本文中一个m×n的二维矩阵代表了一个粒子，则适应度函数执行一次的时间复杂度是O （m2×n），在求解的过程中的时间复杂度是O （m2×n×t）。本文引入了最优渐进式变异算子，根据上文表述可知其时间复杂度是O （m2×n×p），其中p是最优粒子的个数，在每次迭代中，最优粒子数目都是在变化的，则在求解过程中的时间复杂度是O（m2×n×p×t）。综上，本文算法的时间复杂度是O （m2×n×p×t）。

3.6 粒子位置初始化

实践表明：根据先验知识对粒子位置进行初始化，能够生成适应度较高的初始粒子群，能够提高算法的收敛速度和收敛率。本文根据最大需求最小冲突的思想，对文献［11］的初始化方法进行了简化：对一个小区，在可用的频率中找到一个不与其它小区冲突的频率，从这个频率开始按照频率号递增和递减交替形成频率分配表，再按照小区的需求进行分配。此方法可有效的提高初始种群的质量，和其它初始化方法相比，此方法更易实现。

3.7 本文算法步骤

（1）设置算法的参数，设置粒子数目、最大迭代次数、以及c1，c2，c3的初始值，根据本文的方法初始化粒子的位置。

（2）根据式 （5）或式 （6）计算粒子的适应度，更新粒子的局部最优值和全局最优值。

（3）根据式 （11）判断当前粒子是否出现聚集，若出现聚集按式 （12）的变异概率对最优粒子执行最优渐进式变异；若未出现聚集执行步骤 （4）。

（4）根据式 （3）形成粒子的新速度。

（5）根据式 （4）得到粒子的新位置。

（6）终止条件判断，若已寻找到最优个体或者达到最大迭代次数，则算法结束，否则执行步骤 （2）。

4 仿 真

本文算法采用MATLAB语言编写，21小区问题的兼容矩阵和需求向量见文献 ［5］。本文先设置最大迭代次数为500，粒子个数为50，c1＝0.9，c2＝0.5，c2＝0.7，α＝0.6，β＝0.4，C＝25，粒子的适应度评价函数是式 （6），进行迭代计算寻找到最小的可用频点数。寻找到最小可用频点数后，粒子的适应度评价函数是式 （5），按照频点数为80、70、52、51、45、42、40进行了100次实验，其他参数不变。

图1给出了以式 （6）为个体的适应度评价函数的仿真图，从图中可见：当迭代进行到第11代时C（P）为0，即出现了满足EMC需求的频率分配方案，此时需要的频点数为57。随着迭代的继续进行，系统所需的最小频点数仍然在降低，最终收敛于42。因此，系统所需要的最小频数应该在42左右。

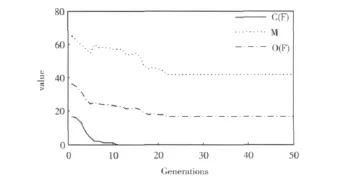
图1 寻找最小可用频点数的进化曲线

图2给出了可用频点数为51的仿真图，采用DPSO算法时，经过13次迭代，历时4.3秒求得一个最优解。采用本文算法时，经过6次迭代，历时3.9秒求得一个最优解。本文采用的最优渐进式变异算子增加了算法每次迭代的时间，但是减少了算法的迭代次数。综合来说本文算法耗时略小于DPSO算法。由图2可见，在2秒之前，DPSO算法和本文算法均未收敛，这是由于本文采用的粒子位置初始化方法增加了粒子初始化时的时间。

由表1可见，在频点数为40时，本文算法仍能达到100%的收敛，即由本文算法求得的最小频点数为40，远远优于文献 ［12］中求得的51个频点。表1中，采用DPSO算法时，随着可用频点数的降低，算法的收敛率在逐渐降低，而算法的平均收敛代数并没有明显的变差，和其它算法相比，粒子群算法能够迅速收敛。当频点数为51时，文献 ［12］的平均收敛代数为54.5，DPSO算法的平均收敛代数为10.2，而本文算法的平均收敛代数为仅为5.5。采用了本文的IDPSO算法后，收敛率得到了显著的提升，收敛代数也略有提高。本文中参数C需要合理的设置，C设置的过大在每一代进化中都要对最优个体进行变异操作，必然会增加算法的运算时间，C设置的过小就不能使粒子跳出局部最优值。

图2 可用频点数为51的仿真

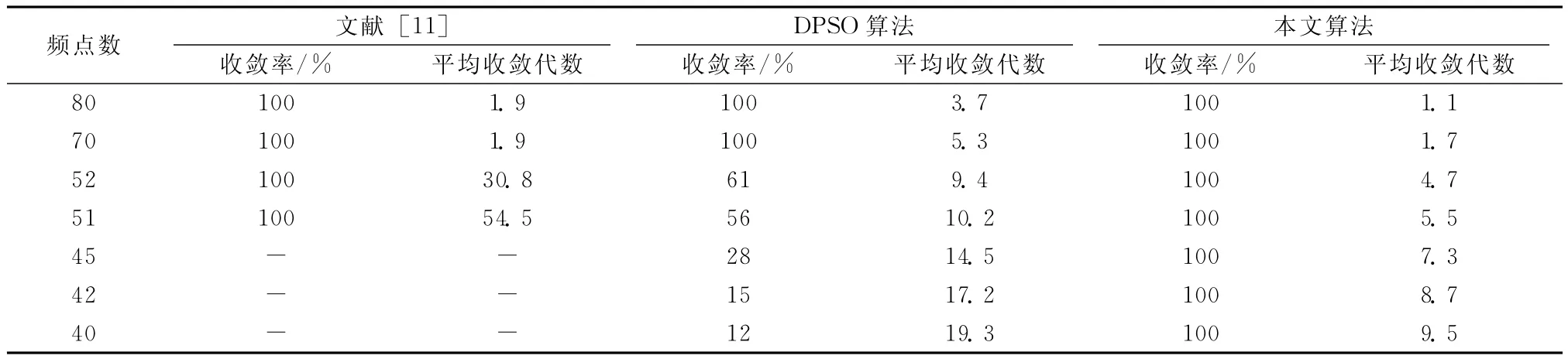
表1 算法仿真结果比较

5 结束语

本文对离散粒子群算法做了改进，在每代最优粒子中引入最优渐进式变异算子，增加了粒子的多样性，提高了算法的抗早熟能力。采用了最小间距编码，压缩了求解空间，加快了算法收敛。将改进的离散粒子群算法用于频率分配问题上，仿真结果表明此算法能够较好的解决该问题，在收敛率和收敛速度上优于离散粒子群算法和混洗蛙跳算法。

文中参数C需要合理的设置，C设置过大会增加算法的运行时间，C设置的过小会降低算法的抗早熟能力。简单合理的设置参数C是一项值得进一步研究的问题。

［1］ZHANG Chunfang，CHEN Juan.Solving frequency assignment problem using an adaptive multi colony ant algorithm ［J］.Mini－Micro Systems，2006，27 （5）：837－741 （in Chinese）.［章春芳，陈娟.求解频率分配问题的自适应的多种群蚁群算法 ［J］.小型微型计算机系统，2006，27 （5）：837－741.］

［2］ZHU Xiaojin，CHEN Yanchun，SHAO Yong，et al.Stepped annealing chaotic neural network model for the channel assignment problem ［J］.Journal on Communications，2008，29（5）：122－127 （in Chinese）. ［朱晓锦，陈艳春，邵勇，等.面向信道分配的分段退火混沌神经网络模型 ［J］.通信学报，2008，29 （5）：122－127.］

［3］SAN Joserevuelta L M.A new adaptive genetic algorithm for fixed channel assignment ［J］.Information Sciences，2007（177）：2655－2678.

［4］KIM Visale，LIU Wei，CHEN Xiaohui，et al.Distributed constraint satisfaction of an improved channel assignment approach in cellular network ［J］.Computer Science，2012，39（6）：81－83 （in Chinese）. ［韦沙，刘威，陈小惠，等.蜂窝网中基于分布式约束满足算法的改进信道分配 ［J］.计算机科学，2012，39 （6）：81－83.］

［5］XU Junjie，XIN Zhanhong.A frequency assignment approach based on microcanonical annealing algorithm ［J］.Journal of Beijing University of Posts and Telecommunications，2007，30 （2）：67－70（in Chinese）.［徐俊杰，忻展红.基于微正则退火的频率分配方法 ［J］.北京邮电大学学报，2007，30 （2）：67－70.］

［6］YU Shicai，WEI Xingang.Channel assignment strategy combining guard channel with queuing ［J］.Computer Engineering and Applications，2012，48 （1）：112－113 （in Chinese）. ［於时才，魏鑫刚.保护信道和排队相结合的信道分配策略 ［J］.计算机工程与应用，2012，48 （1）：112－113.］

［7］JIANG Fu，PENG Jun.Dynamic channel assignment based on swarm intelligence in emergency communication ［J］.Application Research of Computers，2012，29 （6）：2293－2296 （in Chinese）.［蒋富，彭军.应急通信系统中基于集群智能的动态 信 道 分 配 ［J］. 计 算 机 应 用 研 究，2012，29 （6）：2293－2296.］

［8］Benameur L，Alami J，El Imrani A.A new discrete particle swarm model for the frequency assignment problem ［C］／／IEEE International Conference on Computer Systems and Applications，2009：139－144.

［9］GAO Guang’en，LIU Quanli，WANG Wei.Multi－channel assignment algorithm of industrial wireless networks based on discrete particle swarming optimization ［J］.Control and Decision，2012，27 （5）：697－702 （in Chinese）. ［高广恩，刘全利，王伟.基于离散粒子群优化的工业无线网多信道分配算法 ［J］.控制与决策，2012，27 （5）：697－702.］

［10］ZHONG Xiangyuan，JIN Min，ZHONG Xiangqian，et al.Channel assignment in cellular network based on self－adaptive genetic algorithm ［J］.Computer Enginee－ring，2010，36（17）：189－191 （in Chinese）.［仲向远，金敏，仲向前，等.基于自适应遗传算法的蜂窝网络信道分配 ［J］.计算机工程，2010，36 （17）：189－191.］

［11］LIU Hongbo，WANG Xiukun，TAN Guozhen.Convergence analysis of particle swarm optimization and its improved algorithm based on chaos ［J］.Control and Decision，2006，21（6）：636－640 （in Chinese）.［刘洪波，王秀坤，谭国真.粒子群优化算法的收敛性分析及其混沌改进算法 ［J］.控制与决策，2006，21 （6）：636－640.］

［12］HE Di，JIA Zhenhong.Frequency allocation approach based on shuffled frog－leaping algorithm ［J］.Computer Engineering，2011，37 （21）：133－135 （in Chinese）. ［何迪，贾振红.基于混洗蛙跳算法的频率分配方法 ［J］.计算机工程，2011，37 （21）：133－135.］