二阶混合型方程的边值问题

闻国椿，许克明，杨广武

（1.北京大学 数学科学院，北京 100871；2.河北科技大学 数学系，河北 石家庄 050018）

1 关于混合型方程边值问题的提出

设D是复平面C上具有边界∂D＝F∪L的单连通有界域，这里（0＜α＜1）是具有端点z1＝一1＋i，z2＝1＋i的一条曲线，L＝L1∪L2，L1＝｛x＋y＝－2，－1≤x≤0｝，L2＝｛x－y＝2，0≤x≤1｝是内两特征线族，而z0＝jy0是L1与L2的交点，又，其中.本文中的符号与参考文献［6－12］中的相同。我们分别在D＋中使用复数x＋iy和复函数w（z）＝u（z）＋iv（z），而在内使用双曲数x＋jy和双曲函数w（z）＝u（z）＋jv（z），其中带有条件j2＝1的j叫作双曲单位。不失一般性，我们可以假定边界Γ是一条光滑曲线，具有形式和在z＝z1，z2处垂直于抛物线这是一条在z＝z1，z2的导数分别为1／2和－1／2的曲线，该曲线可以通过共形映射实现。我们于内考虑二阶线性混合型方程

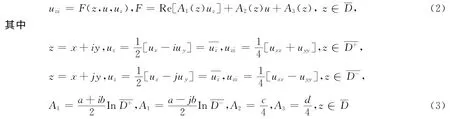
假定方程（2）满足下面的条件，即

条件C方程（2）中的系数Al（z）（l＝1，2，3）在D＋是可测的，而在内是连续的，还满足

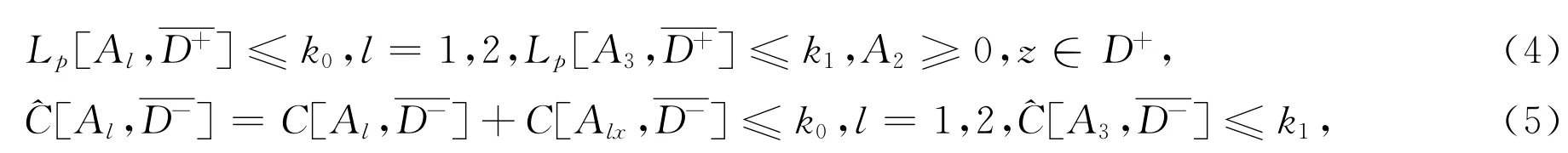
其中p（＞2），k0，k1都是正常数。如果条件（5）由下述所代替：

此处α（0＜α＜1）是一个实常数，则条件将被称为条件C′。

问题P求方程（2）在内一个连续可微解，其在¯D内是连续的，且满足边界条件

其中ν是在Γ∪L2上的每一点处的已给向量，满足条件λ（z）＝a（x）＋ib（x）＝cos（ν，x）－icos（ν，y），z∈Γ，λ（z）＝a（z）＋jb（z）＝cos（ν，x）＋jcos（ν，y），z∈L2，b0，b1，b2都是实常数，而λ（z），r（z），b0，b1满足条件

其中n是在Γ上每一点的外法线向量，α（0＜α＜1），k0，k2是正常数。为方便起见，我们可以假定b1＝0，否则通过一个函数变换这个要求就可以被实现。根据文献［7］第V章第1节，可以看出上述问题P包括Tricomi问题作为其特殊情况，由于Tricomi问题的边界条件如下：

方程（2）带有条件A3（z）＝0，r（z）＝0和b0＝b1＝b2＝0的边值问题称为问题P0.数

称为问题P和问题P0的指数，其中

其中t1＝z1，t2＝z2.这里，我们在D＋的边界∂D＋上选K＝0.若在Γ上cos（ν，n）＝0，并且值u（z0）＝b2可以被u（z1）所确定，即

简言之，我们选取K＝0，点条件是

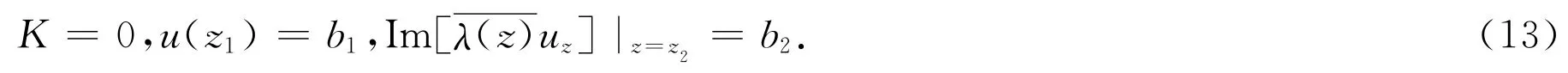
如果我们选指数K＝－1／2，则（7）中的第二个点条件可以取消。这就是上述边值问题适定性的一种提法（参看文献［10］第Ⅱ章）。

假定在D＋内置w（z）＝uz＝［ux－iuy］／2，在内置uz＝w（z）＝［ux－juy］／2，很明显方程（2）的问题P等价于一阶混合型复方程和边界条件

的Riemann－Hilbert边值问题（问题A）。根据文献［7］公式（2.10），我们看出上述积分在D内与积分路径是无关的，并且u（z）内在内是连续可微的。

2 混合型方程边值问题解的表达式与唯一性

现在我们给出方程（2）的解的表示定理。

定理1设方程（2）在D＋内满足条件C，u（z）是方程（2）在内一个连续解，并且在内是连续可微的，其可从式（15）和式（16）推导出来。则u（z）可以被表示为

此处ψ（z），Ψ（z）是D＋内方程（2）的解，并且

在Γ∪S上，它们分别满足边界条件

这里ψ（z），Ψ（z）满足估计式

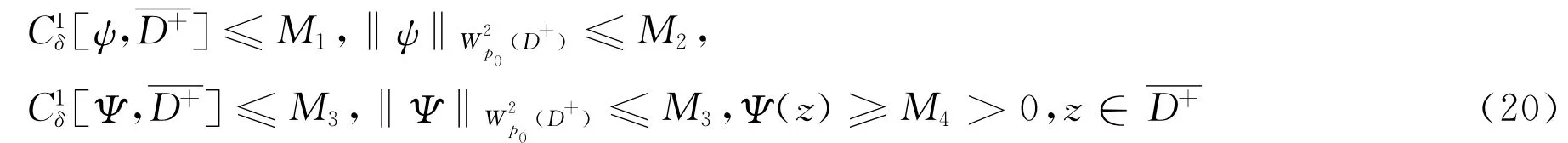
其中δ（0＜δ≤α），p0（2＜p0≤p），Ml＝Ml（p0，δ，k，D）（l＝1，2，3，4）是正常数，k＝（k0，k1，k2）.此外U（z）是方程

的解，其中Im［φ（z）］＝0，z∈Sandφ（z）满足估计式

此处δ（0＜δ≤α），M5＝M5（p0，δ，k0，D）是正常数。φ（z）在D＋内是解析的。如果u（z）是方程（2）在D＋内满足边界条件（7）和

的一个解，则下述估计成立：

其中k3是一个正常数，s（x）如同后面的（33）式所述，并且

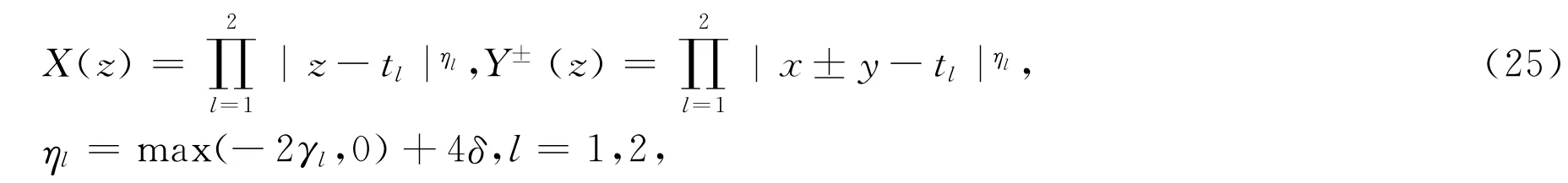
这里γl（l＝1，2）是（11）式中所示的实常数，而δ是一个充分小的正常数，又M6＝M6（p0，δ，k0，D＋）也是正常数。

证明根据文献［11］定理2.1.2证明中的方法，在D＋内方程（2），（18）分别有解ψ（z），Ψ（z），它们满足边界条件（19）和估计（20）。不难看出

是方程（21）的解，且w（z）可以表示成公式（17）的第二式，其中φ（z）满足如（22）式的估计，且Φ（z）是D＋内的解析函数。如果（23）式中的s（x）是一个已知函数，则边值问题（2）、（7）、（23）有唯一解u（z），如（17）式中所示，它满足估计式（24）。

定理2设方程（2）满足条件C，则方程（2）的问题P的任意解可表示为

此处在D＋内及内，而w0（z）在D内是复方程

带有边界条件（7），（8）（w0（z）＝u0z）之问题A 的一个解，且W（z）具有形式

的解，这里（30）的第二式中的λ（z）＝1－i，z∈S，而（30）式的第三式中λ（z）＝1－j，z∈S，又s（z）可由以下公式（33）表出。此外，根据文献［7］第Ⅳ章定理2.2，方程（27）问题A 的解w0（z）和u0（z）满足如下形式的估计式

其中w±（z）＝Rew（z）±Imw（z），X（z），Y±（z）如前所述，且

此处M7＝M7（p0，δ，k0，D）是一个正常数。由（32）式可得出如下

其中M8＝M8（D）是一个正常数。

证明令u（z）是方程（2）的问题P的一个解，且将w（z）＝uz，u（z）代入（29）式中w，u的位置，这样在（28），（29）式中，在内的函数和在内的Ψ（z）都可被确定。此外，我们可以找到方程（27）具有边界条件（30）在D＋内的解˜Φ（z）和在内的解Φ（z）。于是在S＝｛－1≤x≤1，y＝x2｝上，有

上述函数类似于文献［7］第Ⅴ章中的公式（2.33）。这里及后面，在L2上有R（z）＝，因而求得复方程

关于问题A 的解

此解如（28）式所示，又u（z）是方程（2）的问题P的一个解，如（26）式中的公式所示。

定理3若方程（2）满足条件C，则方程（2）的问题P在D 内最多有一个解。

证明令u1（z），u2（z）是方程（2）的问题P的两个解。根据条件C，我们看出u（z）＝u1（z）－u2（z），且w（z）＝uz满足齐次方程和边界条件

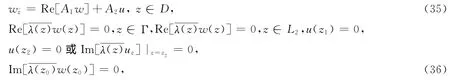
根据定理2，解w（z）可以表示为如下形式

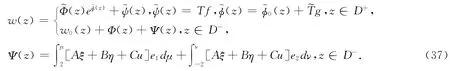
其中g（z）如（29）中所示,是D＋内的一个解析函数，且Φ（z）是方程（27）在内满足边界条件（30）的一个解，具有类似于定理1中φ（z），ψ（z）的性质。若D＋内A2＝0，则.此外，函数在S上满足边界条件

利用逐次逼近法并注意到

这里M0＝M0（D）是一个正常数，于是可得估计式

的解，其中λ（z）＝1－i，z∈S.类似于文献［10］第Ⅱ章定理1.4的证明，利用椭圆型方程解的极值原理，我们可以得到在内u（z）＝0.这表明方程（2）的问题P的解的唯一性。

3 混合型方程边值问题的可解性

定理4假定混合型方程（2）满足条件C，则方程（2）的问题P在D 内有一个解。

证明显然方程（2）的问题P等价于一阶复方程

和边界条件

以及关系式（16）的问题A.根据（16）式得出

其中X（z），Y±（z），w±（z）如（31）中所述，M8＝M8（D）是一个正常数。下面，应用逐次逼近法，我们将找到在D 内复方程（42）的问题A 的解。首先用方程（27）的问题A 的解w0（z）（＝ξ0e1＋η0e2）和（32）中的u0（z），代入到方程（42）右半部的w（＝ξe1＋ηe2）和u（z）的位置，类似于文献［7］第Ⅳ章定理4.2，文献［11］第Ⅱ章定理2.3.1的证明，我们有相应的函数f1（z），g1（z）,和

其中μ＝x＋y，ν＝x－y，这里Φ1（z）是内方程（27）满足边界条件

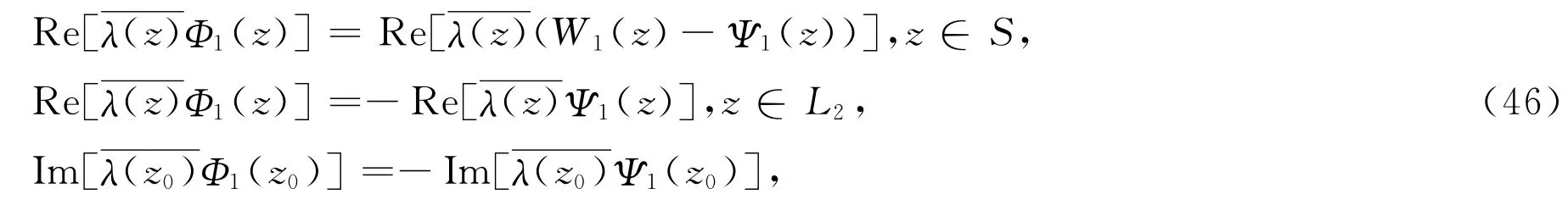
满足估计式

进而把w1（z）＝w0（z）＋W1（z）和相应的函数w1（z），ξ1（z）＝w＋（z）＝Rew1（z）＋Imw1（z），η1（z）＝w－（z）＝Rew1（z）－Imw1（z），u1（z）分别代入到（26），（28），（29）中w（z），ξ（z），η（z），u（z）的位置，类似于（45）－（47）式，我们可以找到内相应的函数以及相应的函数Φ2（z），W2（z）＝Φ2（z）＋Ψ2（z），并且函数

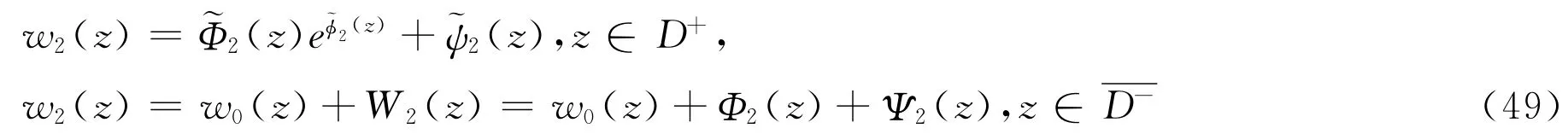
满足类似（48）形式的估计式。于是存在一个函数序列：｛wn（z）｝，也就是

此处n＝1，2，… 从上述等式和

这里M0＝M0（D）是一个正常数，我们可以得到估计式

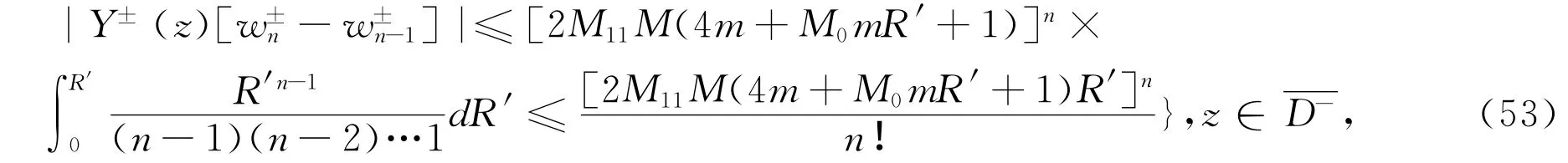
这样相应的函数u＊（z）恰是方程（2）在区域内的问题P的解，且w＊（z）满足估计式

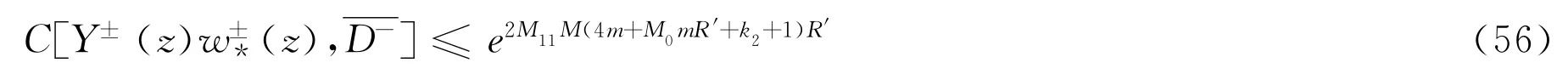
同时我们可以得到估计式

因此从序列｛X（z）wn（z）｝，我们可以选出一个子序列，在内一致收敛于X（z）w＊（z），并且w＊（z）满足相同的估计式（57）。联合（56）和（57），显然看出方程（2）的问题A在内的解满足估计式

其中M13是一个正常数。此外（17）中的函数u（z）是方程（2）的问题P 的解，这里w（z）＝w＊（z）.

从定理3和4我们看出：在条件C情况下，方程（42）的问题A有唯一解w（z），它可以用逐次逼近法找到，并且相应的问题P的解u（z）满足估计

其中X（z），Y±（z）如（31）中所述，且Ml＝Ml（p0，δ，k，D），（l＝14，15）都是正常数，k＝（k0，k1，k2）.

此外，我们可以推出下述定理。

定理5假定方程（2）满足条件C，则方程（2）的问题P的任意解u（z）满足估计

其中Ml＝Ml（p0，δ，k0，D）（l＝16，17）都是正常数。从估计式（58）、（59），我们看到方程（2）的问题P的解的正则性。

［1］Bers L..Mathematical aspects of subsonic and transonic gas dynamics［M］.New York，Wiley，1958.

［2］Bitsadze A.V..Some classes of partial differential equations［M］.New York，Gordon and Breach，1988.

［3］Rassias J.M..Lecture notes on mixed type partial differential equations.Singapore，World Scientific，1990.

［4］Smirnov M.M..Equations of mixed type.Providence，RI，Amer.Math.Soc.，1978.

［5］Sun H.S..Tricomi problem for nonlinear equation of mixed type［J］.Sci.in China（Series A），1992，35，14－20.

［6］Wen G.C.，Begehr，H..Boundary value problems for elliptic equations and systems.Harlow，LongmanScientific and Technical Company，1990.

［7］Wen G.C..Linear and quasilinear complex equations of hyperbolic and mixed type.London，Taylor ＆Francis，2002.

［8］Wen G.C..Conformal mappings and boundary value problems，Translations of Mathematics Monographs106.Providence，RI，Amer.Math.Soc.，1992.

［9］Wen G.C..Solvability of the Tricomi problem for second order equations of mixed type with degeneratecurve on the sides of an angle［J］.Math.Nachr.，2008，28，1047－1062.

［10］Wen G.C..Elliptic，hyperbolic and mixed complex equations with parabolic degeneracy.Singapore，World Scientific，2008.

［11］Wen G.C.，Chen D.C.，Xu Z.L..Nonlinear complex analysis and its applications，Mathematics Monograph Series 12.Beijing，Science Press，2010.

［12］Wen G.C..Recent progress in theory and applications of modern complex analysis［Z］.Beijing，Science Press，2008.