基于距离的K－Means划分式聚类算法及其编程实现

马宝秋，连翠玲，赵 旭

（1.石家庄职业技术学院 机电工程系，河北 石家庄 050081；2.河北省科学院自动化研究所，河北 石家庄 050091）

俗话说：“物以类聚，人以群分”，在自然科学和社会科学中，存在着大量的分类问题。

类，就是指相似元素的集合。聚类就是按照事物间的相似性进行区分和分类的过程，实际就是一种分组的过程。聚类分析又称群分析，它是研究（样品或指标）分类问题的一种统计分析方法，可以作为其他分析算法的一个预处理步骤。聚类同分类不同，聚类并不关心某类是什么。聚类的目标只是把相似的东西聚到一起，因此一个聚类算法通常只需要知道如何计算相似度就可以了。

聚类分析以相似性为基础，其由若干模式组成。这里的“模式”是指根据一个度量标准所得到的结果。在一个聚类中的模式之间比不在同一聚类中的模式之间具有更多的相似性，也就是让在同一个聚类集合中的成员对象都有相似的一些属性。所以，聚类分析主要依赖于对被观测对象间的接近程度或相似程度的理解，例如对象间的距离，颜色相似度等。也正因为如此，定义不同的距离量度和相似性量度就可以产生不同的聚类结果。

聚类分析内容非常丰富，有不同的聚类方法。例如划分法（分割式）、层次法（阶层式）、基于密度的方法、基于网格的方法、基于模型的方法等等［1］［2］。本文所论述的K－Means算法是划分法中的一种。划分式聚类算法在实现时需要首先确定聚类数量和聚类中心位置，然后根据划分原则通过反复迭代运算，逐步降低目标函数的误差值，使聚类中心接近实际聚类中心。当目标函数值收敛时，就会得到最终聚类结果［1］。

1 K－Means算法

给定一个由N 个元素组成的数据集，构造K（K＜N）个聚类，每一个聚类实际就是一个分组。数据对象和分组间满足以下要求：

（1）每一个分组至少包含一个数据对象；

（2）每一个数据对象属于且仅属于一个分组。

对于给定的K个聚类，按照给出的分组方法规则（算法）通过反复迭代的方式改变分组，使得每迭代一次之后的分组结果都比前一次更接近真实分组情况。我们可以把——同一分组中的数据对象按算法所得到的结果越接近越好，而不同分组中的数据对象按算法所得到的结果越远越好，作为确定接近真实分组的标准［2］。

把N个数据聚类为K类的K－Means算法数学表达如下：

其中：Ji为第i类聚类的目标函数；

K为聚类个数；

Xj为第j个输入向量；

Ci为第i个聚类中心（向量）；

wji为权重（Xj是否属于聚类Ci）。

wji满足以下关系：

因为每个数据对象都有其权重wji，这样就由wji构成了一个矩阵，该矩阵也称为隶属度矩阵。如图1所示为有9个数据，分3个聚类的隶属度矩阵。

图1 隶属度矩阵

K－means算法根据不同应用可以确定不同的算法模式，本数学表达式算法模式是基于求各个数据对象与其对应聚类中心点距离平方和的值最小，属于划分法，也称为C－Means算法。

2 K－Means算法的实现步骤

根据上节K－means数学表达式的算法，可知，按照以下几步即可实现本算法［3］。

步骤1：初步确定聚类中心。随机选取K个数据点Ci，i＝1，…，K，并将之分别视为各聚类的初始中心。

步骤2：根据确定的聚类中心进行分组。也就是根据计算规则判断各数据对象属于哪一个聚类，若某个数据对象Xj被判定属于第i个聚类，则其权重值wji＝1，否则为0。

步骤3：判断聚类中心是否收敛。由（1）式计算目标函数J，如果J的结果保持不变或其变化达到允许的精度范围内，代表聚类结果已经稳定不变或可以接受，则可结束此迭代方法，否则进入步骤4

步骤4：更新聚类中心。以（4）式更新聚类的中心点。回到步骤2

式（4）是通过对（1）式求最小值得到的，若求（1）式最小值，求下式最小值即可：

令F’＝0，则可导出（4）式。

针对二维图像实现K－Means算法编程的计算机伪代码步骤如下［4］：

（1）设定聚类数目K，允许的最大执行步骤tmax和一个很小的容忍误差ε＞0；

（2）随机或人为决定聚类中心起始位置Cj（x，y）0，0＜j≤K；

（3）fort＝1，…，tmax

（A）forj＝1，…，N

（i）计算图像中各点到聚类中心的距离；

（ii）计算各图像点属于哪一聚类（建立隶属度矩阵）；

（B）更新聚类中心；

（C）根据收敛准则计算，若E（t）＝‖J（t）－J（t－1）‖＜ε成立则退出循环，否则进行下一轮迭代。

Nextt

（4）若t循环正常结束，则所得到的Ci（xi，yi），i＝1，…，K，即为每个聚类的中心点。

若t循环是因为达到tmax而结束，则表示所聚类的数据是发散的，没有聚类中心；或者在限定的次数内聚类中心还不稳定，可以采用增大循环次数tmax的方式解决。

笔者通过以上方法实现了基于距离划分的K－Means聚类算法。对于笔者分类应用中的一个结果如图2所示。

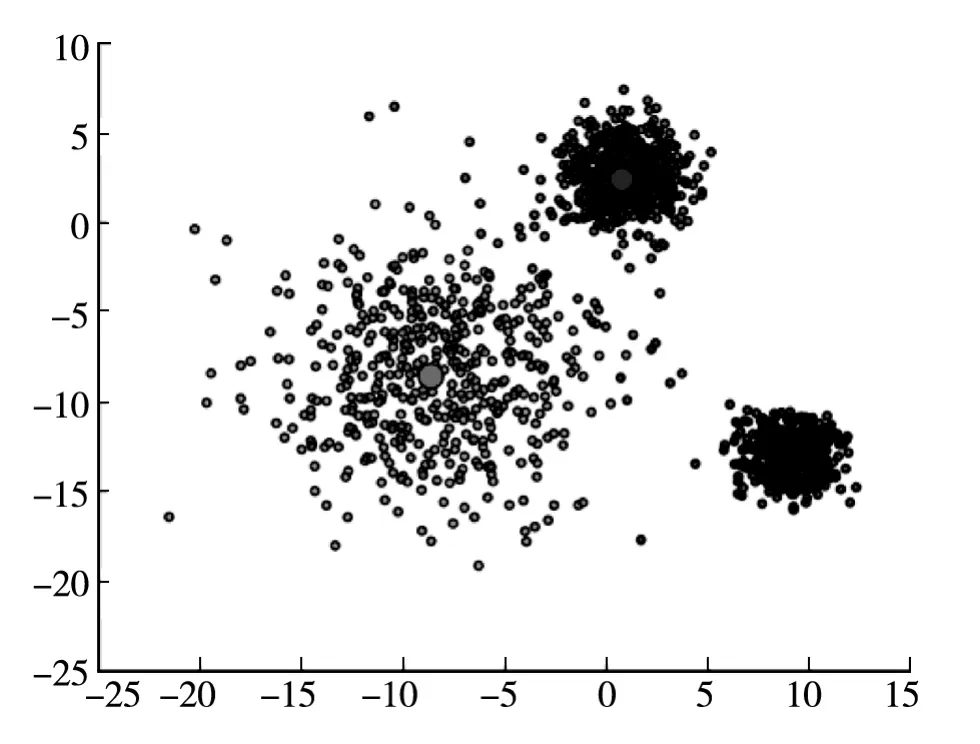
图2 K－Means算法验证

3 算法实现中的注意事项

（1）需先设计数据输入对话框，用来输入聚类的数目K以及容忍误差ε。

（2）通常情况下采用计算机随机函数来产生聚类K个中心，但是针对具体的问题可以有一些启发式的选取方法或者直接人工选取。

（3）计算图像中各点到聚类中心的距离时，使用欧式几何计算2点间距离即可。

（4）隶属度矩阵保存于一个2维数组中。内层j循环每循环一次，根据结果对矩阵中的数值进行相应的修改。

（6）所得到的计算结果是各个聚类分组的几何中心。

4 算法总结

K－Means算法在运算过程中没有任何先验的知识可以应用，因此是一种无监督的分类［1］［5］。每个聚类结果都属于高斯分布。大多数情况下能够给出令人满意的结果，算是一种简单高效应用广泛的聚类方法。

K－Means聚类算法也有其局限的方面。首先，初值的选取对是否能收敛到全局最优解有很大的关系。因为初始聚类中心位置可能是随机函数产生的，即不是理想的位置，使得目标函数J很容易落入局部解，不能保证全局最优，导致分类出来的结果不理想［6］。所以应该多次选取初值运行K－Means，并取其中最好的一次结果。

其次，运算量大，因为每迭代一次就需要遍历所有数据一遍，其运算复杂度为O（tKmn），其中，t为迭代次数，K为聚类数，m为特征属性数，n为待分类的对象数［1］。因此该算法的数值运算量较大，对于大的数据量一般不能进行实时运算。

第三，所产生每个聚类的大小相差不会很大，而且对于噪声数据很敏感。

第四，该算法聚类结果以近圆形为主，对于图3所示的图形就不适合分类了；对于这种情况可以采用基于密度的方法进行分类。这样就能克服基于距离的算法只能发现“类圆形”的聚类的缺点。

最后，该算法是一种硬划分，它把每个待辨识的对象严格地划分到某个类中，具有非此即彼的性质，对于一些特殊的场合就不合适了。

5 结束语

论述了基于欧式距离的划分式K－Means算法，笔者使用C＋＋编程实现本文算法，并应用于“基于实时超声影像的软组织形变跟踪技术”课题软件中，实现了对感兴趣区域（ROI）的前期分类，为后续的图像处理打下了坚实的基础。但由于其固有的缺点，还不能够满足实时性的需要，后续工作中将对其进行进一步的改进以提高系统实时性。

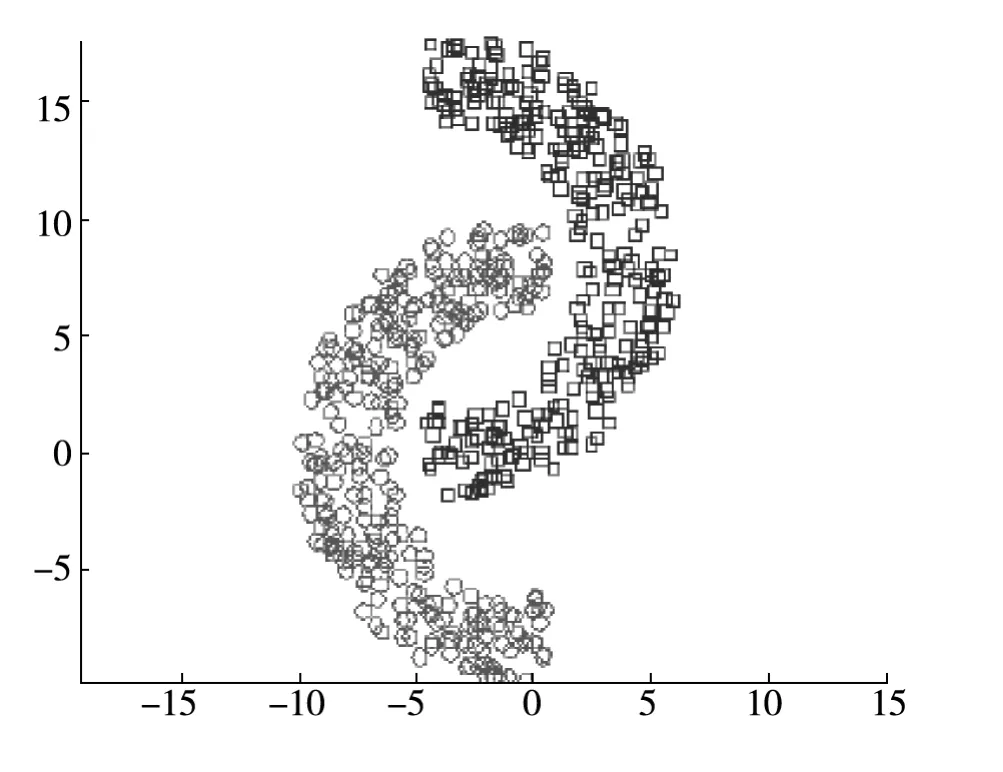
图3 不规则分布数据的分类

［1］孙吉贵，刘杰，赵连宇.聚类算法研究［J］.软件学报，2008，19（1）：48－61.

［2］蔡元萃，陈立潮.聚类算法研究综述［J］.科技情报开发与经济，2007，17（1）：145－146.

［3］步媛媛，关忠仁.基于K－means聚类算法的研究［J］.西南民族大学学报·自然科学版，2009，35（1）：198－200.

［4］陈寿文，李明东.基于面向对象思想K－Means算法实现［J］.滁州学院学报，2008，10（3）：42－44.

［5］杨燕，靳蕃，KAMEL Mohamed.聚类有效性评价综述［J］.计算机应用研究，2008，25（6）.

［6］韩晓红，胡彧.K－means聚类算法的研究［J］.太原理工大学学报，2009，40（3）：236－239.