自适应SAR 图像噪声识别和去噪算法研究

彭 浩，刘明生

（1.石家庄铁道大学 信息科学与技术学院，河北 石家庄 050043；2.石家庄铁路职业技术学院，河北 石家庄 050041）

合成孔径雷达（Synthetic Aperture Radar，简称SAR）是微波遥感的代表。SAR 是主动遥感器，不依靠太阳辐射，可以昼夜工作，即具有全天时的特性［1］。由于SAR 图像的相干成像机制，使得图像内原本具有相同后向散射系数的均质区域表现有颗粒状等噪声，而且在雷达信号受到敌方针对性的电子干扰时，SAR 系统所成的像是模糊的。SAR 图像噪声大大提高了对成像后图像解译的复杂性，降低了对图像分割、目标分类以及其他信息提取的有效性。

对SAR 图像进行干扰的噪声类型有多种。目前对SAR 成像系统能进行干扰的技术方面主要分为压制性干扰和欺骗式干扰。由于不同于常规雷达干扰，对SAR 干扰的结果是反映在成像后的图像上。在图像噪声分类上可主要分为：椒盐噪声、高斯噪声、泊松噪声、斑点噪声、动感模糊、模糊噪声、锐化噪声等7类噪声。因此针对不同类型的噪声干扰信号可采取不同的抗干扰去噪方法。

1 典型的噪声信号类型与特征提取

1.1 数字图像噪声类型

下面将主要考虑7类数字图像的噪声，针对不同噪声图像，实验以圣地亚国家实验室公开的图像来介绍对SAR 图像自适应噪声识别与去噪系统对噪声类型的识别及去噪处理的全过程。（1）椒盐噪声一般可由图像传感器，传输信道，解码处理等产生黑白相间的亮暗点噪声。去噪算法：FRINR［2］。（2）高斯噪声是指噪声的概率密度函数服从正态分布。若高斯噪声的功率谱密度服从均匀分布，则称它为高斯白噪声。去噪算法：模糊自适应加权均值滤波器（Iterative Weighted Maximum Likelihood Denoising With Probabilistic Patch－Based Weights［3］）。（3）泊松噪声一般在照度非常小的时候出现，或在高倍电子放大线路中出现。Poisson噪声就是指围绕拟合线上下波动的大小，其可以用频率公式表示，当取值x不等于0的时候便出现噪声，噪声的大小取决于x可以取多少个数值，和计算出结果与理想曲线之间差距得出。去噪算法：Optimal Inversion of the Anscombe Transformation in Low－Count Poisson Image Denoising［4］。（4）SAR 是基于相干成像技术，而这一技术的理论基础存在着原理性缺陷：在雷达回波信号中，相邻的像素点的灰度会由于相干性而产生一些随机变化，这种随机变化存在某一均值。当接收机连续观测同一地表区域时，具有相同后向散射系数均质区域在SAR 图像中并不具有均匀灰度，呈现出颗粒状起伏，这种即是SAR 相干斑点噪声。去噪算法：2DDFT－DWT。（5）动感模糊是由SAR 雷达设备、物体、背景间沿着两个矢量方向相对运动而造成的。任何沿着SAR 相机相对方向运动的物体将会看起来模糊或被晃动。动感模糊可能发生在高速拍摄移动中的SAR 雷达波被干扰延迟及重放。去噪算法原理可参照文献［5］。（6）锐化噪声可能发生在高速拍摄移动中的SAR 雷达波被干扰重放使得两个相干波叠加。去噪算法可利用快速小波分解算法，将锐化图像分解为高频分量与低频分量，然后利用阈值滤波算法对高频分量进行滤波，同时采用Retinex算法对低频分量图像进行亮度调整。（7）模糊噪声是SAR 雷达设备、物体、背景间沿着单个方向相对运动而造成的效果。任何沿着SAR 相机相对方向运动的物体将会看起来模糊或被晃动。模糊噪声可能发生在高速拍摄移动中的SAR 雷达波被干扰延迟。本噪声去噪算法参照文献［8］。

1.2 干扰信号特征的提取

首先，需要对SAR 图像样本部分数据进行数据归一化，防止图像差异对识别结果造成影响。实验中，选择噪声信号较为敏感的8个特征值（见图1－图8）。本图像噪声的能量熵通过具有旋转不变性的二维Zernike矩的值来体现。引入噪声曲面的以下数学特征：曲面边界法矢、曲面变化率、弹性变化率、曲面能量离散率、外载荷修正量等来识别不同噪声来源。

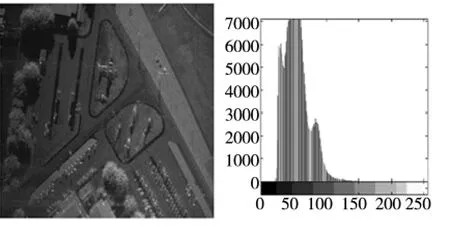
图1 SAR image

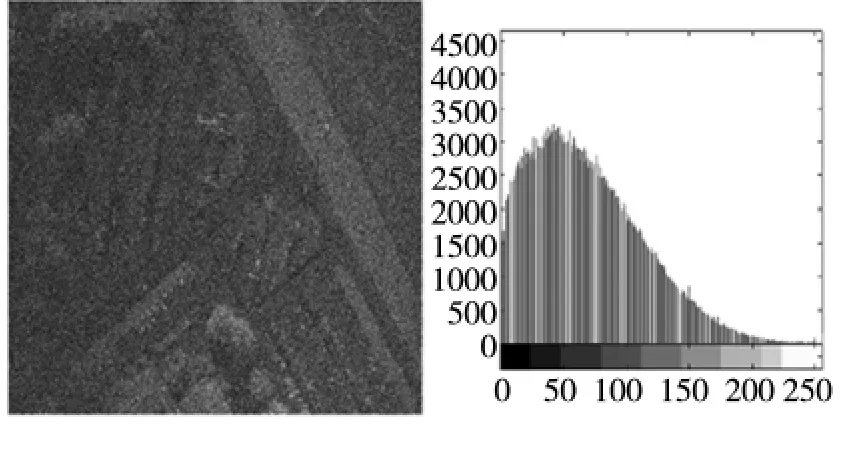
图2 Salt＆Pepper noise image snr＝－5.28db

图3 Gaussian noise image snr＝－1.30db

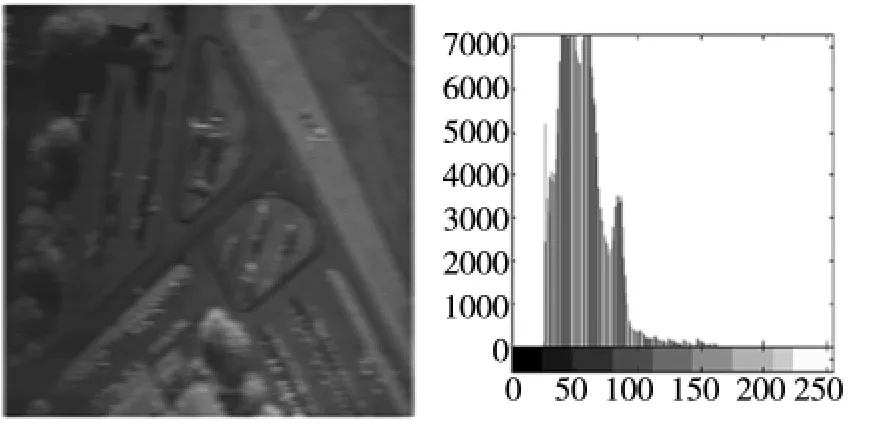
图4 Poisson noise image snr＝36.20db

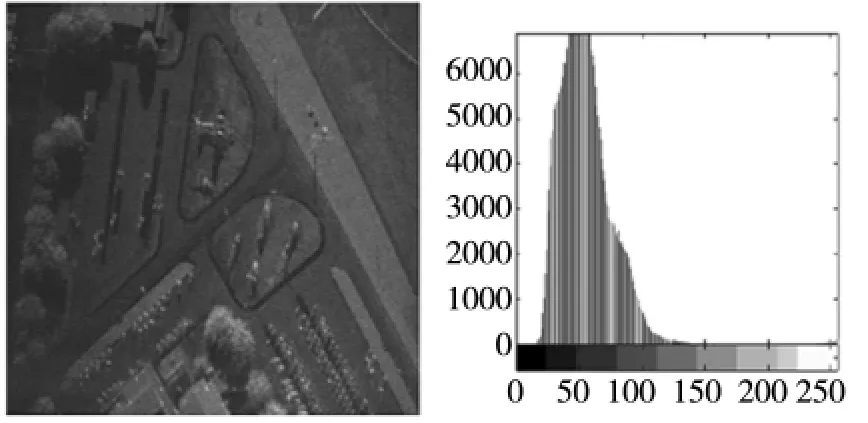
图5 Speckle noise image snr＝－11.84db

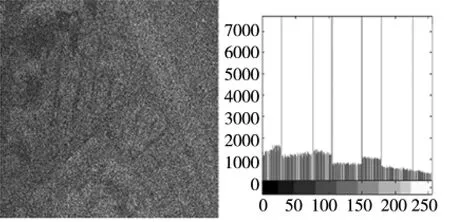
图6 Motion Blur noise image snr＝21.97db

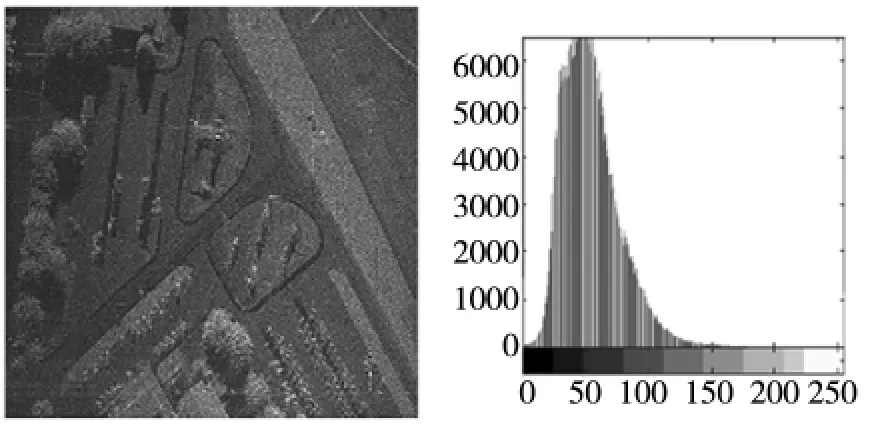
图7 Sharpened noise image snr＝29.70db

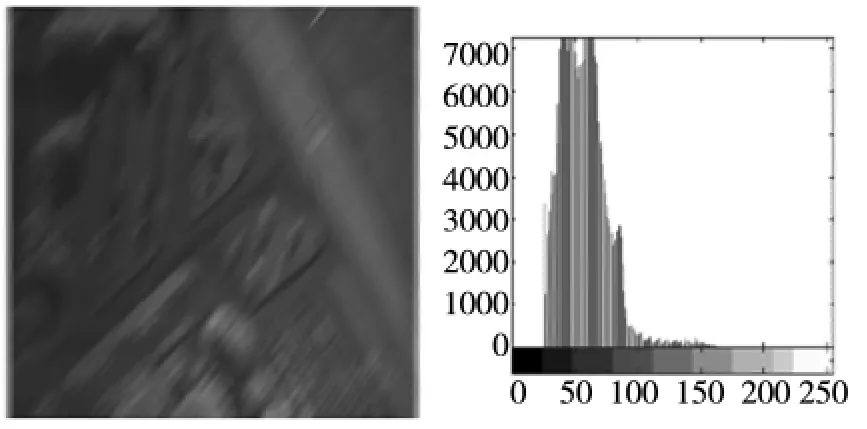
图8 Blur noise image snr＝25.33db

（1）小波高频系数直方图的不显著系数能量比

由小波变换原理，含噪信号的高频部分影响的是小波分解的高频第1层，低频部分影响小波分解后的最深层和其低频层。图象噪声信号主要在各个尺度信号中高频信号部分表现出来。利用小波变换后的高频系数的直方图和曲线拟合图的不同特征表现识别出图像受干扰噪声的类型。对图像进行小波分解后，各子带表征了图像的不同特性.而噪声主要集中在图像的高频子带中即HH 子带。因此分析高频HH 子带是能够识别出噪声类型的。

设HH 子带系数矩阵为D（i，j），然后按系数幅值绝对值的大小划分出较小系数DT（i，j）＝｛｜D（i，j）｜，｜D（i，j）｜＜T｝式中T为判别系数是否是较小系数的阈值，较小系数能量与子带总能量比为：

式中：mun为总的HH子带系数个数，而munT为满足较小系数条件的系数个数［7］。在本文中取该项数值的过程中是将含噪声图像的三维影像分为3个平面图像，并对每一部分进行小波分解，提取第一层分解后的高频信息，在阈值为T＝30时，计算高频系数的较小系数的能量比，得到3个方向上的较小系数能量比。

（2）噪声能量熵分布梯度特征平面Zernike矩

根据噪声图像亮度能量理论，由于亮度反映信号强弱，信息熵反映信息量，因此基于频域的图像能量熵可为噪声能量紊乱和信息冗余提供衡量指标。Zernike矩是一组正交矩，具有旋转不变性的特性，即旋转目标并不改变其模值。由于Zernike矩可以构造任意高阶矩，所以Zernike矩的识别效果优于其他方法［8］。

式中：mn为正整数，n－｜m｜＝偶数，｜m｜≤n；γ是零点到（x，y）的矢量长度，－1＜x，y＜1；Rnm（γ）表示点（x，y）的径向多项式。

下面讨论噪声曲面的边界法矢、曲面变化率、弹性变化率、曲面能量离散率、外载荷修正量等特征值。由Terzopoulos和Gossard借鉴弹性力学中的薄板弹性变形方程，提出了能量优化法创建自由曲面的一般应用模型［6］：

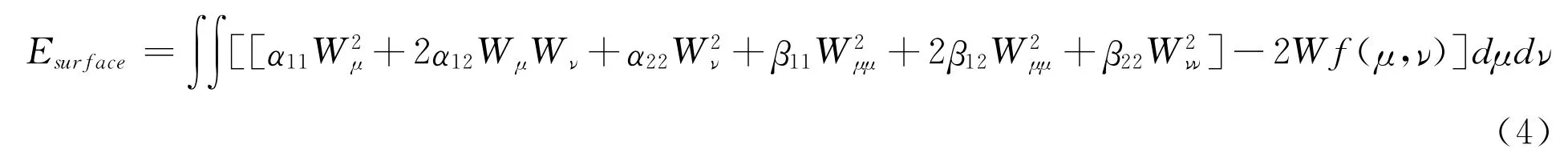
式中：W为所求的以μ，ν为参数的曲面；Wμ，Wν，Wμμ和Wνν分别为曲面沿着μ，ν方向的一、二阶偏导矢，Wμν为混合偏导矢；α，β为材料特性参数，f为外载荷，用以改变曲面形状。在通常情况下未考虑α，β与f的影响，因此材料特性参数均赋为1，外载荷均赋值为0。

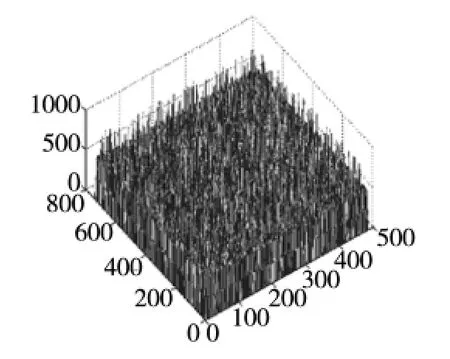
图9 椒盐噪声能量分布图像

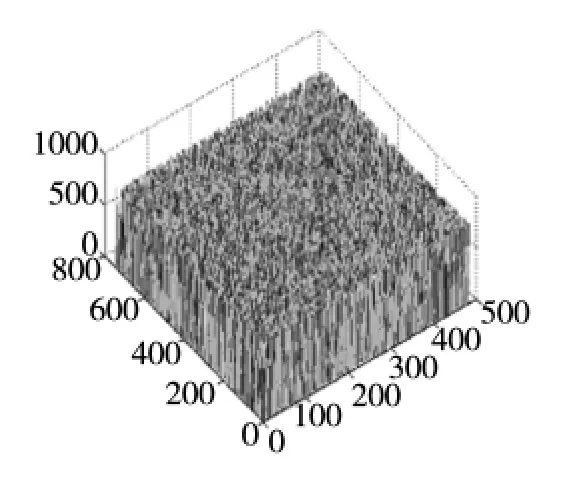
图10 高斯噪声能量分布图像

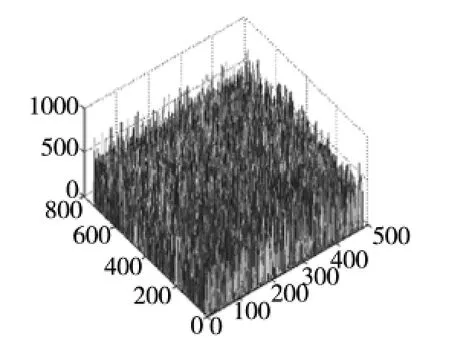
图11 泊松噪声能量分布图像

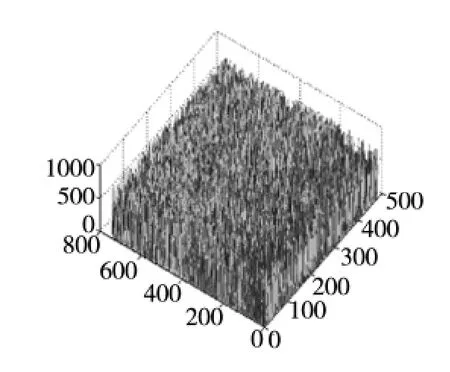
图12 斑点噪声能量分布图像

图13 动感模糊噪声能量分布图像

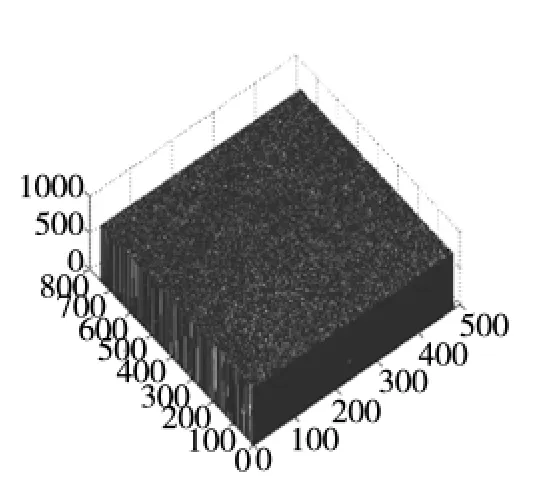
图14 锐化噪声能量分布图像

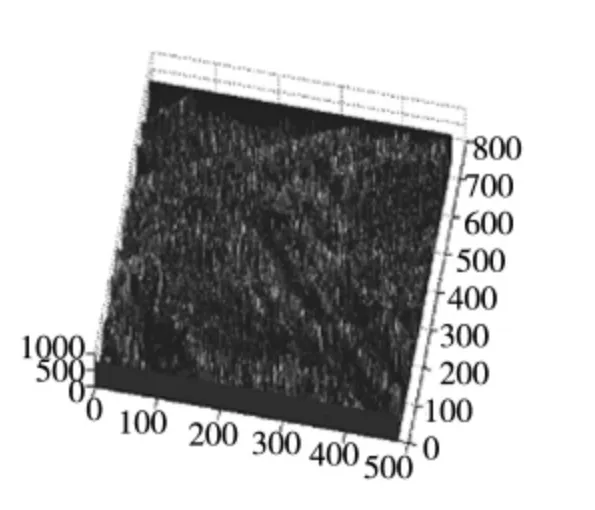
图15 模糊噪声能量分布图像

（3）噪声曲面的曲面边界法矢

式中：Si为曲面上任意三点所组成三角曲面的面积，nj为组成的三角曲面的发矢［9］。

（4）噪声曲面的曲率变化率

式中：ki、kj为沿着主方向ei、ej的主曲率。

（5）噪声曲面的μ、ν向弹性变化率

式中：W为所求的以μ，ν为参数的曲面；Wμ，Wν，Wμμ和Wνν分别为曲面沿着μ，ν方向的一、二阶偏导矢，α，β为给定参数，f（μ，ν）为给定的矢量函数。

（6）噪声曲面的曲面能量离散率

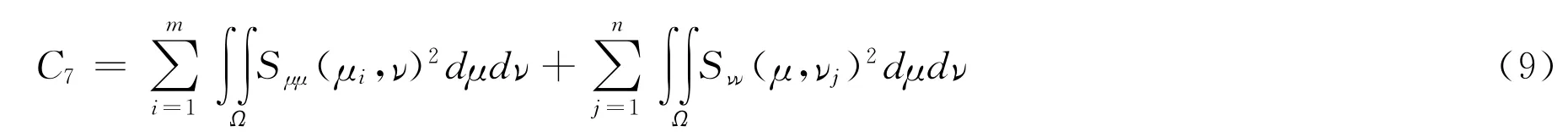
式中：Sμμ（μi，ν）、Sνν（μ，νj）为曲面分别在μ，ν两个方向上的二阶导数。

（7）噪声曲面的曲面外载荷修正量

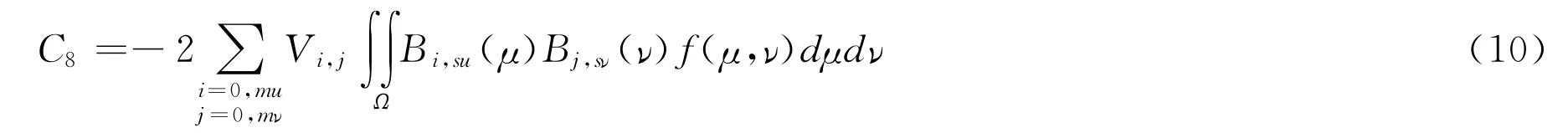
式中：Bj，sν（μ）Bj，sν（ν）分别为曲面沿着μ，ν方向控制参数B样条曲线。

特征向量C将作为BP神经网络分类器的输入向量，对各种干扰进行分类识别。表1为图2至图8的各项实验数据值。

表1 噪声图像的各项特征数据值

2 BP神经网络的SAR 图像噪声干扰信号的识别

BP神经网络是一种多层前馈网络。其主要思想是从后向前（反向）逐层传播输出层的误差，以间接计算出隐层误差。设计BP神经网络分类器使用各项参数为：网络层数3 层（输入层、隐含层、输出层）；10个输入层节点，15个隐含层节点，3个输出层节点。激励函数形式为logistic函数：，式中α＝1，学习系数为0.30，动量因子为0.015，训练步长为0.35，显示间距因子为25。网络输入为100组受上述7类噪声干扰的SAR 图像的7×100组输入域数据。网络输出为由格雷码组成的数字识别系统。在系统识别噪声类型过程中，得到具体的SAR 噪声实际输出向量yi后，求取输出向量参数与每组噪声类型理想参数的马氏距离：

式中，σi是xi的标准差，yi为网络的实际参数向量组（网络实际输出）［y1，y2，y3］，yi∈［0，1］，xi代表7类预定参数（网络理论输出）。在计算出来的7个马氏距离中，以最小的马氏距离值所对应的理想噪声类型作为判断噪声类型的标准。当最小马氏距离和理想目标输出｜dpracticadtheoretical｜≤0.3时，可以判断dtheoretical所对应的噪声类型就是测试图像的噪声类型。对于受到多种噪声污染的SAR 图像也可采用多种过滤去噪算法，对SAR 图像进行综合去噪处理。表2第三列是本文中各种噪声图像在BP网络中的分类数据，第四列为最小马氏距离值。

3 SAR 图像噪声识别率分析

为对新方法进行评价，选择几种典型图像噪声识别算法，对以上样本进行实验，并在计算速度以及识别率两方面进行比较。编程语言选择C＃，实验环境基于.Net4.0＋AForge.NET Framework－2.2.4平台。计算机处理器配置为4核Intel（R）Core（TM）i7－2630QM CPU＠2.00GHz，8G 内存。

表3 算法时间效率比较图

4 SAR 图像选择去噪算法的分析

下面以在过滤高斯噪声方面比较优秀的算法Probabilistic Patch－Based filter（以下简称：PPB filter）为例，来演示根据不同噪声类型采取不同去噪算法和单独使用PPB filter算法的去噪效果图。下面图中左侧为PPB filter算法过滤噪声后的图像，右侧为本文根据不同噪声类型采用不同的相对优秀的算法过滤图像结果图。

图16 Salt＆Pepper denoising image

图17 Gaussian denoising image

图18 Poisson denoising image

图19 Speckle denoising image

图20 Motion Blur denoising image

图21 Sharpened denoising image

图22 Blur denoising image

5 结语

针对7类典型的数字图像噪声污染，在本文中提取了8类SAR 噪声图像特征数据，设计了BP神经网络分类器，引入了格雷码和马氏距离分类来区分不同噪声类型与选择去噪算法。采用了100组含SAR 噪声图像对网络有效进行训练，对噪声图像的识别和去噪的效果比较好，系统可以采用多种算法综合去噪。同时，本系统还有样本数据不够多和综合判断受到多重噪声污染时缺乏理论依据的不足之处。当场景变化大时，识别率会降低，现有噪声干扰的特征值的提取不一定就能有很好的识别，对噪声干扰的研究还需要继续深入。

［1］Ananya Roya and Barry Craverb，Image noise in helium lithography，Science ＆ Technology of Materials，Interfaces，and Processing.

［2］TRIETLE，RICK CHARTRAND，THOMAS J.ASAKI＊J，A Variational Approach to Reconstructing Images Corrupted by Poisson Noise，Math Imaging Vis 27：257－263，2007.

［3］Lukinl，Krivenko1，Zriakhov1，LOSSY COMPRESSION OF IMAGES CORRUPTED BY MIXED POISSON AND ADDITIVE GAUSSIAN NOISE.

［4］Isabel Rodrigues，Jõao Sanches and Jos′e Bioucas－Dias，DENOISING OF MEDICAL IMAGES CORRUPTED BY POISSON NOISE.

［5］Deledalle and R.Willett＿Z.Harmany，POISSON NOISE REDUCTION WITH NON－LOCAL PCA J.Salmon＿C－A.

［6］Markku Mäkitalo and Alessandro Foi，Optimal Inversion of the Anscombe Transformation in Low－Count Poisson Image Denoising，IEEE TRANSACTIONS ON IMAGE PROCESSING，VOL.20，NO.1，JANUARY 2011.

［7］Xiang Zhu and Peyman Milanfar，A NO－REFERENCE SHARPNESS METRIC SENSITIVE TO BLUR AND NOISE.

［8］Zhang Chunxiao，Zhao Yan，Xu Dong，Identification of blur support size in blind image restoration with moderate／intense noise.

［9］Image Thumbnails That Represent Blur and Noise，Ramin Samadani，Senior Member，IEEE，Timothy A.Mauer，David M.Berfanger，and James H.Clark，IEEE TRANSACTIONS ON IMAGE PROCESSING，VOL.19，NO.2，FEBRUARY 2010.