复杂网络的社团结构发现

贾宁宁，封 筠

（石家庄铁道大学 信息科学与技术学院，河北 石家庄 050043）

复杂网络是由数量巨大的节点和节点之间错综复杂的连边共同构成的网络，可以刻画Internet网、交通网、生物信息网、社会交往关系网等等实际系统。社团结构是复杂网络的一个重要拓扑特征，2002年Girvan等提出了社团结构的概念，指出社团内部结构紧密，社团间结构稀疏［2］。揭示复杂网络中的社团结构并对其进行分析是了解现实生活中各种网络组织结构的一种重要途径。根据节点是否属于且仅属于一个社团可将社团分为非重叠社团和重叠社团。本文从社团结构发现的历程角度列出了非重叠社团发现的典型算法，较全面地归纳总结了重叠社团发现算法，并指出了未来新的研究方向。

1 非重叠社团发现技术

复杂网络社团分析早期的研究始于非重叠社团发现，主要是通过发现有效算法，找到网络中相互独立的社团。目前最具有代表性的非重叠社团发现方法有计算机科学中的图分割方法、社会学领域中的层次聚类方法和GN 算法。

1.1 图分割方法

图形分割方法最初用于解决并行计算问题，通常情况下，找到这类分割方法是个NP 难题。随着图的规模不断增大精确解越难得到，但是在试探性算法下可以得到满意解。基于Laplace矩阵的传统谱平分法［1］是典型的试探性算法。该算法的理论基础是同一社团节点对应的Laplace矩阵特征向量的分量较接近。将节点的无向图转化为Laplace矩阵，矩阵的非零向量对应的特征分量元素中，符号相同的属于同一社团。

1.2 层次聚类方法

层次聚类方法最先应用于社会学中，社会分析网络中的层次聚类的思想与复杂网络中社团结构的划分思想很接近，目的是根据节点间的相似度划分网络中的社团结构。该方法根据添加边还是移除边分为聚集（Agglomerative）和分裂（Divisive），其中典型算法为聚集算法［1］，其思想是计算每对节点的相似度，再按相似度从高到低依次合并节点对，形成树状图，可在任意时刻终止合并，得到相应的社团结构。

该算法的特点是在求解社团结构时与原网络拓扑结构无关，拓扑结构仅在计算相似度时运用，缺陷是由于可在任意时刻终止合并，会导致若干节点无法确定归属。

1.3 GN 算 法

Girvan和Newman在PNAS上发表的论文［2］研究了社会网络和生物网络中的社团结构，首次提出社团结构是网络普遍具有的拓扑特征，并给出了基于边介数（边介数为所有节点对之间的最短路径中经过该边的路径数的个数）的分裂式算法以识别网络中的社团结构。GN 算法的思想是计算网络中每条边的边介数，删除边介数最大的边，然后重新计算剩余每条边的边介数，再删除边介数最大的边，可在任意时刻终止删除操作，得到相应的社团结构。

GN 算法是基于删边的分裂式方法，解决了若干节点无法确定归属的问题。缺陷在于要计算重复每条边的边介数，因此计算量较大。

1.4 模块度函数

Newman等提出了模块度［1］的概念大大推动了社团结构的研究，模块度是指网络中连接社团结构内部节点的边所占比例与另外一个随机网络中连接社团结构内部节点的边所占比例的期望值的差值。构造这个随机网络的方法为：每个顶点的社团属性保持不变，节点间的边根据节点的度随机连接。若是社团结构划分得好，则社团内部连接的密集程度会高于随机连接网络的期望水平。模块度的提出也为研究人员提供了一个目标函数，通过比较真实网络中各个社团的边密度和随机网络中对应子图的边密度的差异衡量社团结构的显著性。可以作为网络中非重叠社团划分好坏的一个度量。

网络的所有可能划分数量巨大，找出划分构成的空间里模块度最优的划分是困难的。因此模块度函数的缺陷在于模块度优化困难。

2 重叠社团发现算法

前面介绍的非重叠社团发现技术，都将节点集严格分为相互独立的社团，而真实系统中这种硬性的划分并不能真正地反映出网络中节点与社团之间的实际关系，如蛋白质相互作用网络中蛋白质功能具有多样性，单个蛋白质可在不同的时间空间条件下参与到不同的功能模块中。因此网络中重叠社团的识别能够更真实的反映出网络的结构和性能特征，已成为了社团结构发现的新热点。

2.1 派系过滤算法（Clique Percolation Method，CPM）

Palla等［3］提出的派系过滤算法是首个能够发现重叠社团的算法，指出复杂网络社团结构的一个重要特征是重叠性和嵌套性，认为社团是由一系列相互可达的K－派系（即大小为K 的完全子图）组成。通过合并相邻的K－派系以实现K－派系社团发现，而那些处于多个K－派系社团中的节点即是社团之间的重叠部分。

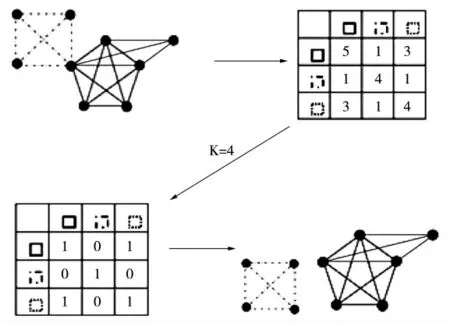
图1 利用K 派系重叠矩阵寻找4派系的社团

图1中左上角的图表示原网络，右上角的图表示该网络的派系重叠矩阵，左下角的图表示对应K＝4的K 派系的社团连接矩阵。右下角是计算结果的K－派系社团连接示意图。

图示寻找4派系的社团步骤为：

（1）找出网络中的K－派系，此处K 取值为5，4；

（2）根据派系间的公共节点数得到重叠矩阵，对角线上元素为派系节点数，非对角线元素为派系间公共节点数；

（3）K 取4，将对角线上小于K 的元素置1，非对角线上小于K－1的元素置0，得到K 派系的社团连接矩阵；

（4）由K－派系的社团连接矩阵得到K－派系社团连接示意图。

派系过滤思想的算法缺陷在于需要以派系为基本单元发现重叠社团，适用于完全子图较多的网络，而对于很多真实网络而言，限制条件过于严格，只能发现少量的重叠社团。

2.2 模糊聚类算法（Fuzzy Clustering Method，FCM）［1］

聚类算法以某种距离为度量将数据分类，模糊算法将求解精确解的问题转化为求解满意解，以隶属度函数为基准去求解问题。将模糊与聚类相结合后的模糊聚类算法通常从构建节点距离出发，再计算节点到社团的模糊隶属度以揭示节点的社团关系。由于模糊聚类算法FCM 本身要求预先知道社团数，因此在模块度Q 值的基础上引入新的模块度指标模糊模块度Q′，选使得Q′值取得最大的模糊聚类结果作为最终的社团划分结果［1］。此类算法的关键在于距离矩阵的构建，需要针对不同的应用选取不同的距离作为度量标准。

2.3 基于种子扩展思想的算法

Lancichinetti等［4］提出以若干个节点为种子，通过扩展形成对整个网络的覆盖，即LMF算法。该算法是首个能够同时找到重叠社团和其层次结构的算法。基于种子扩展算法的思想是通过特定的选择策略，将最大满足选择策略的节点作为种子节点，再根据设定的适应度函数计算其它节点与种子节点的适应度，将适应度最大的节点与种子节点归为一个社团，依次执行以上操作，直到所得到的的社团满足评价函数取得最大值为止。

选用不同的种子选择策略和扩展方式可构成不同的种子扩展算法。如文献［5］以最大中心度节点作为种子选择策略，以适应度进行扩展，通过相似度进行合并得到最终的社团结构。

2.4 基于局部的社团发现［1］

对于很多超大型的网络，特别是动态的网络而言，提前得知其网络拓扑结构花销巨大，基本不可能实现。这时可以从局部出发去挖掘网络的社团结构。基于局部的社团发现算法的思想是从某些特定节点出发，依据给定的算法进行扩展，最终得到满意的社团结构。基于局部的社团发现降低了算法的复杂度，与实际应用需求联系紧密，适用于对万维网的研究。

2.5 边聚类的社团发现

以上四种典型算法都是从节点角度来发现重叠社团，以边为基准来划分社团在近些年得到关注。Evens等人提出通过构建“边图”（以边为节点的图）来发现重叠社团结构［1］。边聚类算法提出的同时，还使得研究者注意到重叠社团中层次性的特性。相对于节点而言，边通常表示某种功能及节点间的某种联系，以边为研究对象可以更准确地揭示出网络的特征和性能结构。

3 总结与展望

除小世界与无标度特征外，复杂网络中社团结构作为一种新的基本特征得到了广泛关注，取得了许多有价值的成果，特别是在社团发现算法方面的研究。本文以社团结构发现的算法为主线，简单回顾了社团结构的研究历程。概要了复杂网络中非重叠社团发现的典型方法和首个用于非重叠社团评价的模块度函数的思想。归纳总结了一些重叠社团发现算法的基本思想及特点，其中基于局部的社团发现和边聚类的社团发现有待进一步深入探讨和研究。

复杂网络的社团结构识别是一个崭新的研究领域，虽然已经提出了一些社团发现算法，但仍然存在着一些开放性的问题需要解决和值得进一步深入研究的方向。

（1）尚无社团和社团结构的定量定义，一定程度上阻碍了社团结构统一的框架和度量标准的形成；

（2）针对重叠社团发现问题，还没有一个合适的评价算法来度量社团的重叠程度，缺乏对算法性能优劣的衡量；

（3）同时揭示重叠社团的层次性、重叠性和嵌套性等特征的算法有待进一步发展；

（4）对于超大规模的复杂网络中社团结构发现算法只是在启发式方法的基础上应用现有的算法，花费的时间比较长，发现超大规模复杂网络中的社团结构算法是个值得深入研究和极具研究价值的方向。

［1］程学旗，沈华伟.复杂网络的社团结构［J］.复杂系统与复杂性科学，2011，8（1）：57－70.

［2］Girvan M，Newman MEJ.Community structure in social and biological networks［J］.Proc Natl Acad Sci USA，2002，99（12）：7821－7826.

［3］Palla G，Derenyi I，Farkas I，et al.Uncovering the overlapping community structure of complex networks in nature and society［J］.Nature，2005，435：814－817.

［4］Lancichinetti A，Fortunato S，Kertesz J.Detecting the Overlapping and Hierarchical Community Structure in Complex Networks［J］.New Journal of Physics，2009，11：033015.

［5］马兴福，王红.一种新的重叠社团发现算法［J］.计算机应用研究，2012，29（3）：844－846.