带分数布朗运动和Markovian跳的种群系统的近优控制*
张启敏,史建伟
(宁夏大学数学计算机学院,宁夏银川 750021)
带分数布朗运动和Markovian跳的种群系统的近优控制*
张启敏,史建伟
(宁夏大学数学计算机学院,宁夏银川 750021)
讨论了一类带有分数布朗运动和Markovian调制的随机种群系统最优逼近控制问题,给出了模型的伴随方程、哈密顿函数,应用Ekeland变分原理、Ito公式及一些不等式给出了随机种群系统最优逼近控制存在的必要条件.
随机种群;分数布朗运动;Markovian链;最优逼近控制;Ekeland变分
1 问题的提出
近年来一些专家建立了确定性的种群模型,并取得一些研究成果[1-3].确定性的种群模型可以由以下偏微分方程来描述:

在上述模型中,Q∶=(0,A)×[0,T],其中t∈(0,T),a∈(0,A),A表示种群的预期寿命,即最大年龄.[r1,r2]表示种群中雌性的生育区间.其余的参数含义如下:K(t,a)为t时刻年龄为a的种群密度;N(t)为t时刻种群的总量;σ(a)表示年龄为a的种群的死亡率;K(t,0)为种群初始分布函数;γ(t)为年龄为t时刻雌性生育率,且0<γ(t)<1;u(t,a)是人为的控制变量;m(t,a)为t时刻年龄为a的种群中雌性所占的比例,I(t,K)表示外界环境对整个种群系统的影响.然而,现实生活中总存在一些不确定性的、不连续的、突然的扰动,如海啸、地震、外来物种的侵入、种群迁徙等等,这些因素的产生致使种群的稳定性受到一定的影响.由于种群系统这种复杂的、受到的影响不连续且不可预测的特性,因此在考虑种群系统的模型时,笔者将分数布朗运动和Markovian链考虑到模型中去,并且假设I(t,K(t,a))被一个随机扰动产生影响,即
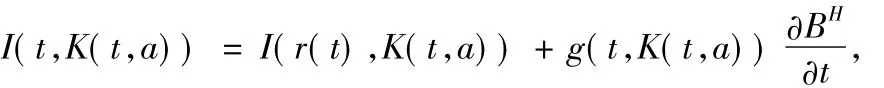
则带有分数布朗运动和Markovian调制的随机资产积累模型有如下表示形式:

目前,关于分别带有Markovian和分数布朗运动的相关研究已经有很多,如文献[4]研究了带有Markovian的随机种群系统的数值解法,文献[5]讨论了一类带有分数布朗运动且与年龄相关的人口模型的数值解,但是对带有分数布运动和Markovian调制的随机扰动的种群系统最优控制的研究并不多见.
众所周知,一般情况下由于最优控制的条件要求比较严格[6-8],所以并不是任何一个问题的最优控制都存在.为此,一些学者便开始研究最优逼近控制[9].笔者主要采用Ekeland变分原理、Ito公式及一些特殊不等式等方法来证明带有分数布朗运动和Markovian调制的随机种群系统的最优逼近控制问题,并给出系统的最优逼近控制存在的必要条件.
2 预备知识
定义1(分数布朗运动)设0<H<1,BH={BH(t),t∈R}是Hurst参数为H的分数布朗运动,其为一连续的高斯过程,是一个半鞅,且满足
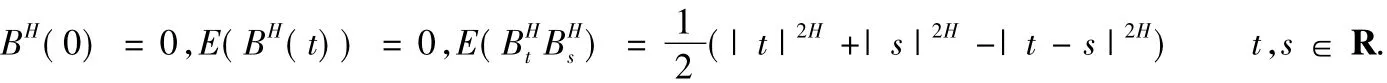
设{r(t),r≥0}是定义在概率空间上取值于有限状态S={1,2,…,N}的右连续的Markovian链,其生成元Γ = (γij)N×N如下给定:


方程(1)的积分形式为

其中Kt=K(t,a).在[0,T]上,考虑如下目标函数:



定义2(ε-最优逼近)[9]对于任一给定的ε>0,设ξ是ε的函数,且满足ξ(ε)→0当ε→0时,此时对于充分小的ε,若|J(uε(·)-V)|≤ξ(ε)成立,则称uε(·)为ε-最优逼近,其中ξ(ε)称为误差阶.若对于一些独立于常数C的δ>0,有ξ(ε)=Cεδ,则称uε(·)为εδ阶的最优逼近.

其中lu(t,K(t,a),u(t,a))是l(t,K(t,a),u(t,a))关于u(t,a)的偏导数.
(H3)(局部利普希茨条件)存在常数C3i>0使得



对任意的u(t,a)∈Uad和其相应的状态变量K(t,a),参照文献[10],引入伴随方程和相应的Hamiltonian函数如下:

显然(λ(t,a),ψ(t,a))是相应于状态过程K(t,a)的伴随过程.很容易看出在(H1),(H2)条件下,伴随方程存在唯一的-适应解(λ(t,a),ψ(t,a),φ(t,a))K(t,a))是有界的,所以存在与K(t,a),u(t,a)独立的常数C4>0,使得伴随过程满足



且对∀v∈V,∀u∈Uad,定义
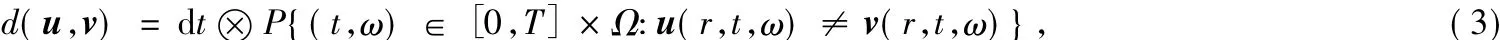
其中dt⊗q是Lebesgue测度dt和概率测度q的乘积测度,显然,(Uad,d)是一个完备的距离空间[11].
3 最优逼近的必要条件
在这一部分,将给出最优逼近控制存在的必要条件.
引理2对∀0<α<1,0≤p≤2,存在常数C1=C1(α,p>0)使得∀u(t,a),u'(t,a)∈Uad以及相应的K(t,a),K'(t,a),有
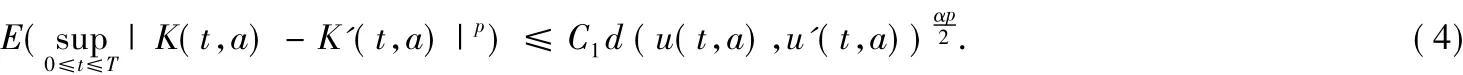
证明首先假设p=2,对|K(t,a)-K'(t,a)|2采用Ito公式,有
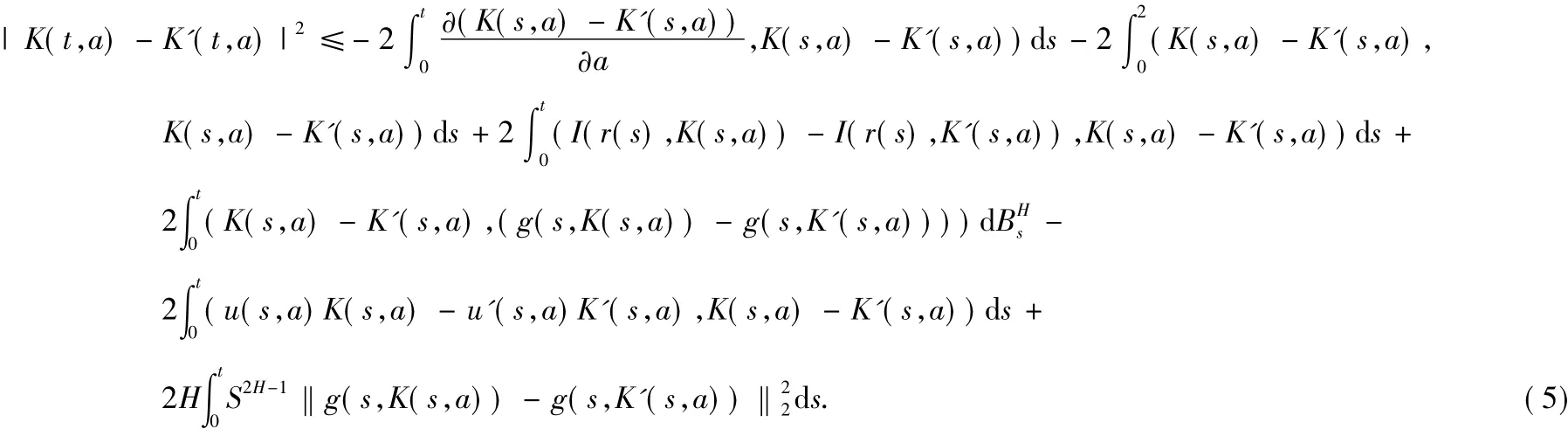
首先来证明(5)式的第一部分.

利用局部利普希茨条件,可得
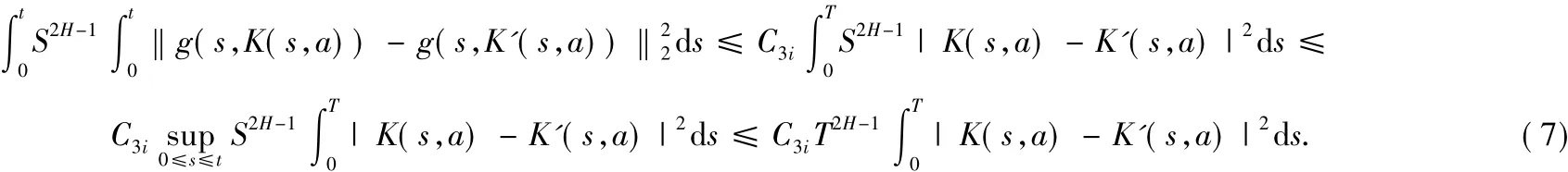
对于(5)式的倒数第三部分,由不等式和定义1可得

C2至C4都是常数.对于(5)式的倒数第三部分,

引理3 对∀0<α<1,1<p<2满足(1+αβ)p<2,存在常数C5=C5(α,β,p)>0,对∀u(t,a),u'(t,a)∈Uad,及相应的状态变量K(t,a),K'(t,a)和伴随变(λ(t,a),ψ(t,a)),(λ'(t,a),ψ'(t,a)),有

证明令((t,a)t,a))≡(λ(t,a)-λ'(t,a),ψ(t,a)-ψ'(t,a)),且满足如下方程:

假设η是如下方程的解:

对任意的向量a≡(a1…an)*有sgn(a)≡(sgn(a1)…sgn(an))*.在(H1),(H2)条件下,方程(10)有唯一的解并且

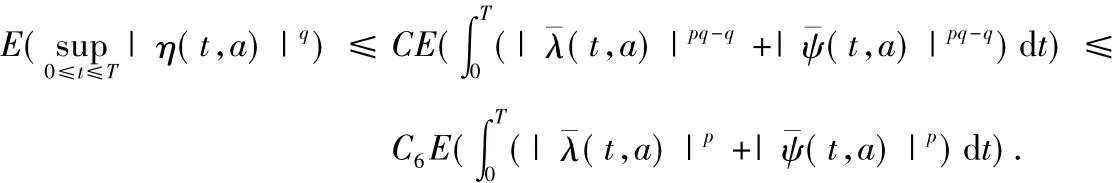
显然由(2)式可知,(10)式右端有界.
另一方面,对¯λ(t,a)·η(t,a)进行Ito积分并取期望,可得

进一步来证明(10)式.首先,

同理,容易得到

由(11),(12)式得到,

综上,(9)式成立,从而引理3得证.
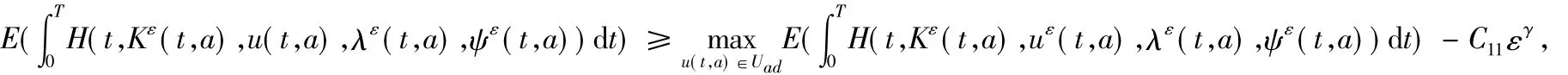
其中Kε(t,a)和(λε(t,a),ψε(t,a))分别为状态方程和伴随方程的解.
证明 现分2步进行.
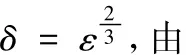
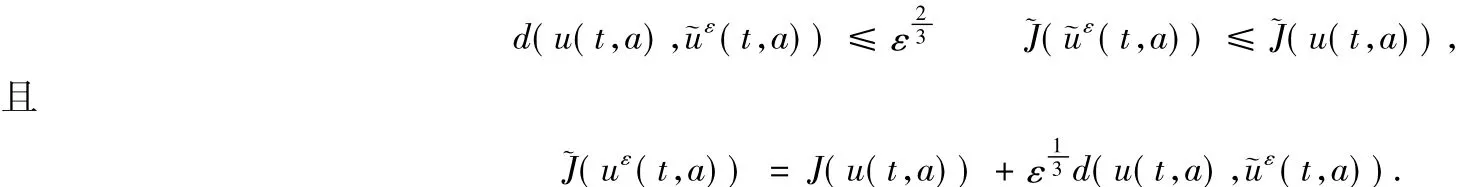

对(14)式按Taylor展开,可得


在(H1)条件下,将(15)式代入(13)式并根据引理1,可得
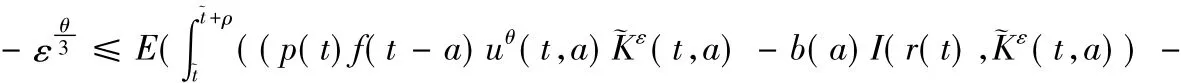

在(16)式中令ρ→0,得到

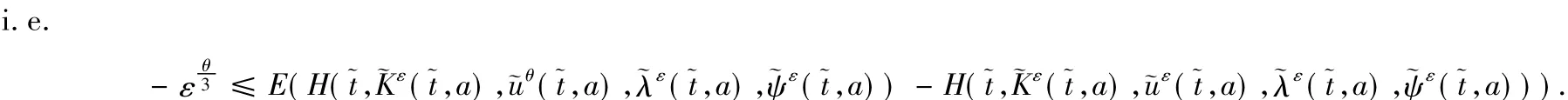
第2步.讨论(Kε(t,a),uε(t,a))成立的必要条件.

综上,关于资产积累系统的最优逼近控制存在的必要性证明完毕.
4 结语
引入一类带有分数布朗运动和Markovian调制的随机种群系统,证明了随机种群系统的最优逼近控制存在的必要.在证明过程中引入伴随方程和哈密顿函数,主要利用Ekeland变分原理、Ito公式以及一些特殊不等式等来证明结论成立.
[1] CHEN Jun-jie,HE Ze-rong.Optimal Control for a Class of Nonlinear Age-Distributed Population Systems[J].Applied Mathematics and Computation,2009,214:574-580.
[2] ZHAO Chun,WANG Mian-sen,ZHAO Ping.Optimal Control of Harvesting for Age-Dependent Predator-Prey System[J].Mathematical and Computer Modelling,2005,42:573-584.
[3] LUO Zhi-xue.Optimal Harvesting Control Problem for an Age-Dependent Competing System of n Species[J].Applied Mathematics and Computation,2006,183:119-127.
[4] ZHANG Qi-min.The Numerical Solutions for Stochastic Age-Dependent Capital System with Markovianswitching[J].Journal of Ecmode,2010(12):143-153.
[5] MA Wen-jun.Numerical Analysis for Stochastic Age-Depedent Population Equations with Fractional Brow-Nian Motion[J].Commum Nonlinear Sci.Numer.Simulat.,2012,17:1 884-1 893.
[6] XU Zhen.Stochastic Maximum Principle for Optimal Control Problem of Forward and Backward[J].Aust.Math.Soc.Ser.B,1995,37:172-178.10.
[7] BAHLALI K,MEZERDI B,OUKNINE Y.The Maximum Principle for Optimal Control of Diffusions with Non-Smooth Coefficient[J].Stoch Rep.,1996,37:303-316.
[8] ELLIOTT R J,KOHLMANN M.The Variational Principle and Stochastic Optimal Control[J].Stochastic Verlag,1999(3):1 -4.
[9] ZHOU Xun-yu.Stochastic Near-Optimal Controls:Necessary and Suffcient Conditions for Near-Optimality[J].STAM.J.Control Optim,1998,36(3):917-929.
[10] YONG Jiong-min,ZHOU Xun-yu.Stochastic Controls,Hamiltonian Systems and HJB Equations[M].New York:Springer Verlag,1999.
[11] MEZERDI B.Necessary Conditions for Optimality for a Diffusion with Non-Smooth Drift[J].Stochastic,1988,24:305-320.
(责任编辑 向阳洁)
Near-Optimality in Stochastic Control of Stochastic Age-Dependent System with Markovian Switching and Fractional Brownian Motion
ZHANG Qi-min,SHI Jian-wei
(School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China)
A class of stochastic age-dependent system with Marvokian switching and fractional Brownian motion is introduced,and the necessary conditions for near-optimality are established.The conditions are described by an adjoint process and a nearly maximum condition on the Hamiltonian.The proof of the main results is based on Ito formula,Ekeland’s variational principle and some estimates on the state and the adjoint process with respect to the control variable.
stochastic age-dependent system;fractional Brownian motion;markovian switching;near-optimal;ekeland’s variational principle
O211.63
A
10.3969/j.issn.1007-2985.2013.02.002
1007-2985(2013)02-0005-07
2012-12-06
国家自然科学基金资助项目(11061024;11261043)
张启敏(1964-),女,天津人,宁夏大学数学计算机学院教授,博士,博士生导师,主要从事随机计算及其
应用研究.

