关于正定Hermite矩阵迹的不等式*
宋 园,周其生
(1.安庆师范学院数学与计算科学学院,安徽安庆 246133;2.滁州职业技术学院,安徽滁州 239000)
关于正定Hermite矩阵迹的不等式*
宋 园1,2,周其生1
(1.安庆师范学院数学与计算科学学院,安徽安庆 246133;2.滁州职业技术学院,安徽滁州 239000)
研究了正定Hermite矩阵迹不等式的问题,在2个已知实数不等式的基础上,利用Neumann不等式,得到了2个正定Hermite矩阵迹的不等式.
不等式;正定Hermite矩阵;迹
矩阵不等式的研究在现代数学中发挥着重要的作用.矩阵的迹是矩阵重要的数字特征,在实际问题(如滤波、随机控制以及计量经济学等)中有广泛的应用.关于矩阵迹的不等式也不断地有新的成果出现.关于正数的不等式,能推广到矩阵的非常少,如:对于任意2个实数a,b有a2+b2≥2ab,而任意2个半正定Hermite矩阵A和B,A2+B2≥2AB一般不成立,重要原因是矩阵的乘法不具有交换性;又对2个半正定Hermite矩阵A与B,一般也不能由A≥B推出A2≥B2.不过,对于矩阵的迹,情况要好得多,这也是人们对研究矩阵迹不等式感兴趣的另一个原因.
1 问题的提出
最近文献[1-2]分别研究了将某些实数不等式推广为矩阵迹和范数的不等式,其中2个不等式如下:
定理A[1]设A与B为n×n正定Hermite矩阵,则tr A2B-1+tr A-1B2≥tr A+tr B,当且仅当A=B时不等式取等号.
定理B[2]设A与B为m×m阶正定Hermite矩阵,则

当且仅当A=B时不等式等号成立.
上述2个矩阵迹不等式是针对一对正定Hermite矩阵给出的,笔者进一步研究上述不等式,将它推广到n个矩阵的情形.
2 相关定义和引理

若λ1,λ2,…,λn为A的特征值,则

注1矩阵迹满足线性性,即
引理1[4](Neumann不等式)设A与B为n阶Hermite阵,它们的特征值分别为λ1≥λ2≥…≥λn和 μ1≥μ2≥…≥μn,则


引理3[2]设a>0,b>0,则有an+bn≥akbn-k+an-kbk(1≤k≤n-1)成立,当且仅当a=b时等号成立.
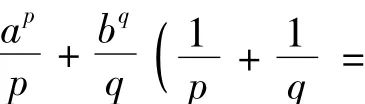
3 主要结果及证明
引理2推广到多个实数的情形也是成立的,于是得到下面的引理:
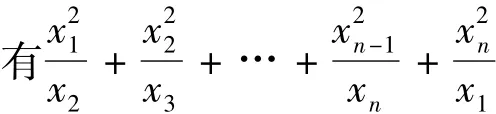

定理1设A1,A2,…,An为n个m×m正定Hermite矩阵,则
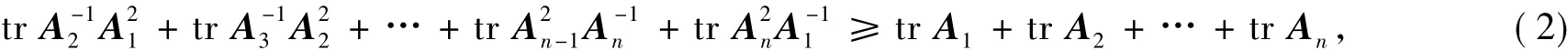
当且仅当A1=A2=…=An时取等号.
证明令Ak的特征值是λ1(Ak)≥λ2(Ak)≥…≥λm(Ak)>0,k=1,2,…,n,则A-1k的特征值为
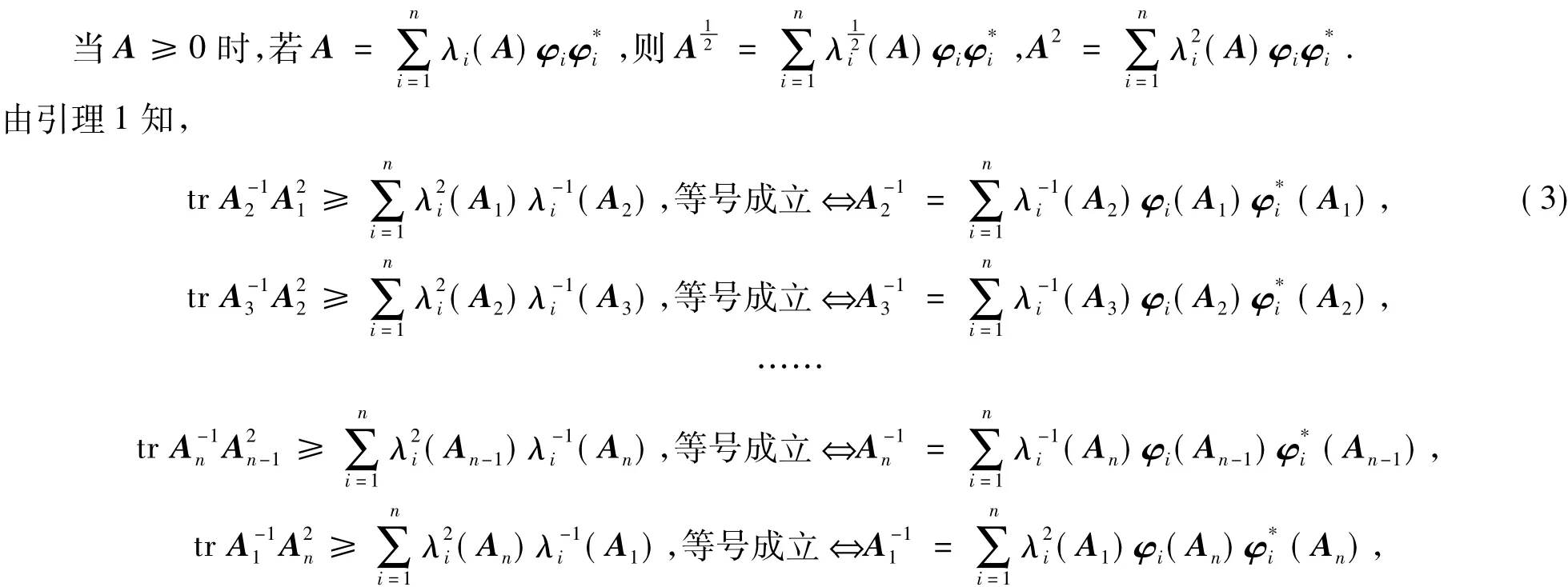
其中φi(Aj)为Aj对应于λi(Aj)的某一组标准正交化特征向量(i=1,2,…,m;j=1,2,…,n).
将以上各不等式两边分别相加,并应用由引理5,可得

又由引理5,(4)式第2个不等式等号成立当且仅当λi(A1)=λi(A2)=…=λi(An),i=1,2,…,m.再由(3)式即得=,从而A2=A1.依次推得A3=A2,…,A1=An.因此,(2)式当且仅当A1=A2=…=Am时取等号.证毕.
引理3推广到多个实数的情形也是成立的,于是得到如下引理:
引理6设a1,a2,…,an>0,则有++…+≤a+…+,1≤k≤n-1,当且仅当a1=a2=…=an等号成立.
证明用引理4可得

当且仅当a1=a2=…=an时等号成立.
文献[2]将an+bn≥akbn-k+an-kbk推广到矩阵中得到迹的不等式tr An+tr Bn≥ t r AkBn-k+t r An-kBk,进一步,将引理6推广到矩阵中得到如下结果:
定理2设A1,A2,…,An为n个m×m正定Hermite矩阵,则
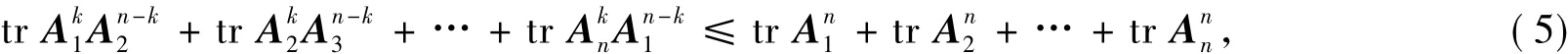
当且仅当A1=A2=…=An时取等号(1≤k≤n-1).
证明因为A1,A2,…,An为正定Hermite阵,所以,…,也为正定Hermite阵.设Ai的特征值为λj(Ai)(i=1,2,…n;j=1,2,…,m),并设φj(Ai)(i=1,2,…,n;j=1,2,…,m)为Ai的对应于λj(Ai)的某一组标准正交特征向量.由引理1和引理6得,


下面讨论等号成立的充分必要条件.

(6)式成立等号当且仅当以上各充要条件均成立.而从引理6可知,(7)式成立等号当且仅当λi(A1)=λi(A2)=…=λi(An),i=1,2,…,m,再结合以上各充要条件得(5)式等号成立当且仅当A1=A2=…=An.证毕.
3 结语
在2个实数不等式的基础上,将它推广到矩阵的迹的不等式中.进一步的工作是能否将这些实数不等式推广到矩阵的范数、矩阵的奇异值、矩阵的特征值中.
[1] 魏 禹,桂 楚,周其生.一个实数不等式在矩阵论中的推广[J].安庆师范学院学报,2011(4):101-103.
[2] 胡 汭,周其生.关于正定矩阵幂的乘积的一些不等式[J].安庆师范学院学报,2012(2):44-46.
[3] 王松桂,吴密霞,贾忠贞.矩阵不等式[M].第2版.北京:科学出版社,2006:129.
[4] BHATIA R.Matrix Analysis[M].New York:Springer,1997.
[5] 匡继昌.常用不等式[M].第3版.济南:山东科学技术出版社,2004:393.
[6] FENG Tian-xiang,LIU Hong-xia.Several Results on the Trace of Hermite Positive Definite Symmetric Matrix[J].数学杂志,2012(2):263-268.
[7] WANG Bo-ying,ZHANG Fu-zhen.Trace and Eigenvalue Inequalities for Ordinary and Hadamard Products of Positive Semidefinite Hermitian Matrices[J].SIAM Matrix Anal.Appl.,1995,16:1 173-1 183.
[8] 张 瑞,周其生.关于Hermite矩阵迹的不等式的几点注记[J].安庆师范学院学报,2011(4):1-3.
(责任编辑 向阳洁)
Two Notes on the Inequalities of Positive Definite Hermite Matrix Trace
SONG yuan1,2,ZHOU Qi-sheng1
(1.School of Mathematics and Computational Science,Anqing Teachers’College,Anqing 246133,Anhui China; 2.Chuzhou Vacational and Technical College,Chuzhou 239000,Anhui China)
In this paper,we study the ineqeality’s problem for the trace of positive definite Hermite matrix.Based on two results of real inequalities,together with Neumann inequality,two inequalities of positive definite Hermite matrix trace are obtained.
inequality;positive definite Hermite matrix;trace
O151.21
A
10.3969/j.issn.1007-2985.2013.02.005
1007-2985(2013)02-0022-04
2012-10-19
安徽省高校省级自然科学基金项目(KJ2012Z300)
宋 园(1982-),女,安徽滁州人,滁州职业技术学院助讲,在职硕士研究生,主要从事矩阵理论研究.

