地震作用下相邻结构间阻尼器的优化参数研究

黄 潇，朱宏平

(1.华中科技大学 土木工程与力学学院，武汉 430074;2.华中科技大学 控制结构湖北省重点实验室，武汉 430074)

现代城市人口密集而土地有限，以致很多建筑结构建造得越来越靠近。当强震发生时，相邻建筑结构间可能会发生碰撞［1］。若采用耗能减震装置来连接相邻结构，既可吸收部分地震能量，又能避免结构间的碰撞。相邻结构耗能减震体系已在多个实际工程中得到了广泛的应用，例如我国的上海国际贸易大厦，采用40个粘滞流体阻尼器将裙房与主结构连接起来，减小了裙房结构的地震扭转效应［2］。在相邻结构振动控制体系中，阻尼器的参数选取是非常重要的。原有的相邻结构间阻尼器的优化参数都是通过繁琐的参数化研究得到的［3-4］，但这种方法不具有通用性。因此若能采用通用的解析表达式来直接计算得到阻尼器的优化参数，这对于相邻结构振动控制体系的应用推广非常必要。

Zhu等推导出了白噪声激励下，两单自由度结构间连接的Kelvin型粘弹性阻尼器［5］和Maxwell型粘滞流体阻尼器［6］的优化参数理论表达式，阻尼器的优化参数可直接由相邻单自由度结构的质量和自振频率得到。朱宏平等［7］将两平行结构简化为两单自由度体系，用Voigt粘弹性阻尼器模型表示被动连接单元，运用Kuhn-Tucker优化原理导出了随机激励下连接单元的优化刚度和优化阻尼的一般表达式。Bhaskararao等［8］推导出了白噪声激励下，对应于不同控制目标的双体单自由度体系间粘滞流体阻尼器的优化阻尼的理论表达式。上述所作研究均是基于双体单自由度结构进行的，结构模型均过于简单。Zhu等［9］将基于相邻单自由度结构体系推导的阻尼器优化参数表达式推广到了相邻多自由度结构体系，得出阻尼器的优化参数与相邻结构的第一阶自振频率和总质量有关的推论。但上述结论仅限于单一场地条件同一地震强度作用下的相邻线弹性结构。对于不同场地特性不同强度地震作用下的相邻结构，阻尼器优化参数表达式的适用性是一个值得关注的问题。本文首先采用随机振动的虚拟激励法，研究了小震作用下相邻结构处于线弹性状态时阻尼器优化参数的取值，详细分析了结构模态阻尼比和场地条件的变化对阻尼器优化参数的影响，并与理论表达式算得的优化值进行了比较;其次采用Bouc-Wen模型模拟结构的滞回特性，分别采用时域和频域分析方法研究了强震作用下结构进入弹塑性状态时阻尼器优化参数的取值，与理论值进行了对比分析;最后对阻尼器的控制性能作了详细的评价。

1 相邻结构计算模型

图1是层数分别为n1和n2的相邻高层建筑结构采用阻尼器连接的示意图，阻尼器在同一标高楼板处水平连接两结构。采用两种类型的阻尼器进行连接，分别为粘弹性阻尼器和粘滞流体阻尼器。

图1 相邻结构简化模型Fig.1 Simplified model of adjacent structures

1.1 阻尼器计算模型和优化参数理论表达式

1.1.1 粘弹性阻尼器

粘弹性阻尼器采用Kelvin模型模拟，阻尼器输出力表达式为f(t)=kdΔx(t)+cdΔ(t)，其中kd和cd分别为阻尼器的刚度和阻尼，Δx(t)和Δ(t)分别为阻尼器两端的相对位移和相对速度。

(1)控制目标1:使结构1的平均相对振动能量最小

设β=ω2/ω1为结构2和结构1的第一阶自振频率比，μ=m1/m2为结构1与结构2的总质量比，则阻尼器的优化刚度系数βopt与优化阻尼系数Δopt表达式如下［9］:

当β≤1时，

当β＞1时，

(2)控制目标2:使相邻结构总的平均相对振动能量最小

将刚度较大的结构1视作主结构，刚度较小的结构2视作从结构，限制结构2与结构1的频率比β≤1，对于β＞1只需将结构1与结构2角色互换。阻尼器的优化刚度系数βopt与优化阻尼系数Δopt表达式为［9］:

当μ＜1时，

当μ≥1时，

可算得Kelvin型粘弹性阻尼器总的优化刚度与优化阻尼分别为:

1.1.2 粘滞流体阻尼器

(1)控制目标1:使结构1的平均相对振动能量最小［9］

阻尼器的优化阻尼系数ξopt与优化松弛时间系数χopt的表达式分别为:

当β≤1时，

当β＞1时，

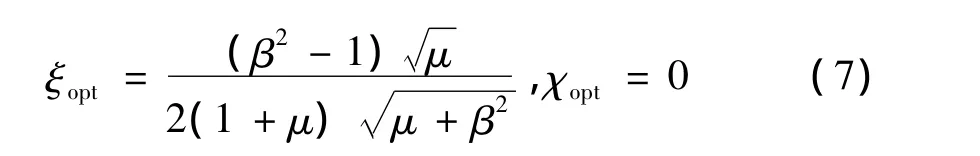
(2)控制目标2:使相邻结构总的平均相对振动能量最小

限制结构2与结构1的频率比β≤1，β＞1需将结构1与结构2角色互换。则阻尼器的优化阻尼系数ξopt与优化松弛时间系数χopt表达式分别为［9］:

当μ≥1时，

当 μ＜1且β2＜μ(2μ-1)/(2-μ)时，

当 μ ＜1且 β2≥μ(2μ-1)/(2-μ)时，

可算得Maxwell型粘滞流体阻尼器总的优化零频率阻尼与优化松弛时间为:

对于两种类型的阻尼器，当Kelvin型阻尼器的优化刚度kd取为0时，阻尼器的输出力表达式为f(t)=cdΔ(t);当Maxwell型阻尼器的松弛时间λ取为0时，阻尼器的输出力表达式为f(t)=c0Δ(t)。二者形式一样，阻尼器的输出力表达式均为阻尼与阻尼器两端相对速度的乘积，此时两种阻尼器可统一为线性流体阻尼器。

1.2 层间恢复力模型

本文考虑了结构处于线弹性状态和弹塑性状态两种情况，层间恢复力fji表达式给出如下。

对于线性层间恢复力，fji=kji(xji-x(j-1)i)，其中kji为结构i第j层的层间刚度，xji是第j层的位移。对于非线性的层间恢复力，采用Bouc-Wen模型模拟［10］，fji的表达式为:

式中:αji为j层屈服后刚度与屈服前刚度的比值;yji=xji-x(j-1)i为第j层的层间相对位移;zji为层间滞回位移;dji为层间屈服位移;Aji、βji、γji和 ηji为控制滞回曲线的参数。按照等效线性化理论，假设yji和zji为联合高斯过程，则滞变位移可作如下线性化处理［11］:

式中:ceji和keji为等效参数。当ηji=1时，等效参数的表达式为:

等效线性化后，滞变系统的运动方程可表示成状态方程的形式。然后通过迭代求解Lyapunov方程来得到等效参数中的响应统计量。

2 结构运动方程

地震激励下，Kelvin型阻尼器连接的相邻结构振动控制体系的运动方程为:

式中:M、C和K为结构体系的n×n(n=n1+n2)维质量、阻尼和刚度矩阵;阻尼矩阵C采用瑞利阻尼模型;Cd和Kd为阻尼器的阻尼和刚度矩阵;X(t)为n维位移向量(t)为地震动加速度;I为n维单位列向量。该运动方程采用状态方程表达如下:

对于Maxwell型阻尼器连接的相邻结构的状态方程和结构随机响应的计算可参考文献［9］。

3 数值算例

某两相邻高层建筑结构，结构1与结构2的层数分别为25层和15层，层高均为3.3 m。各楼层集中质量取为1.56×106kg，剪切刚度均为4.0 ×109N/m。则结构1与结构2的第一阶自振频率分别为3.12 rad/s和5.17 rad/s。采用瑞利阻尼模型，设结构的第一、二阶模态阻尼比相同，均为0.02。过滤白噪声参数取为ωg=15.6 rad/s与 ζg=0.6，地面运动激励强度S0取为4.65×10-4m2/rad·s3，假设在此地震强度激励下并且由于阻尼器的耗能作用，两结构仍处于线弹性阶段。在本文中阻尼器仅布置在相邻结构的第8层和第15层，各个阻尼器的参数均相同。

3.1 结构模态阻尼比的变化对阻尼器优化参数的影响

为了研究结构模态阻尼比的变化对阻尼器优化参数的影响，将结构1和结构2的模态阻尼比分别取为0.02和0.05。图2中给出了当两结构的阻尼比均为0.02时，结构的振动能量均方差随Kelvin型阻尼器总的刚度kd的变化曲线。从图中可以看出，对应于控制目标1，当kd小于临界值4.0×106N/m时，阻尼器的刚度对控制效果影响很小;对应于控制目标2，当kd小于临界值8.0×106N/m时，阻尼器的刚度对控制效果几乎没有影响。但当kd的取值超过临界值后，结构的振动能量会随着kd的增加急剧增大。

图3给出了当结构1的阻尼比为0.05、结构2的阻尼比为0.02时，结构的振动能量均方差随Maxwell型阻尼器总松弛时间λ的变化曲线。从图中可以看出，当λ增加时，结构的振动能量均方差仅略微增大，可见Maxwell型阻尼器的松弛时间对结构控制效果影响很小。当结构1与结构2的阻尼比均为0.02时，请参考文献［9］。可看出当结构的阻尼比取不同数值时，结构振动能量随总松弛时间λ的变化规律是相同的。

从图2和图3可以看出，Kelvin型阻尼器的刚度和Maxwell型阻尼器的松弛时间在较大范围内变动时，对控制效果影响很小，因此Kelvin型阻尼器的优化刚度kd与Maxwell型阻尼器的优化松弛时间λ均可取为0。采用理论表达式算得的kd和λ也均为0，二者的计算结果是一致的，此时两种类型的阻尼器均变为经典的线性流体阻尼器。图4中给出了当结构1和结构2的阻尼比分别取为0.02和0.05时，结构振动能量均方差随Kelvin(Maxwell)型阻尼器的阻尼cd(c0)的变化曲线。从图中可以看出，当结构的模态阻尼比变化时，阻尼器的优化阻尼不变。对于控制目标1，优化阻尼约为5.0×107N·s/m;对于控制目标2，优化阻尼约为4.5×107N·s/m。对于控制目标1和控制目标2，采用Kelvin(Maxwell)型阻尼器优化参数表达式算得的优化阻尼分别为4.80×107N·s/m 和4.43×107N·s/m，可见参数化研究值与理论值吻合的非常好。可得出，虽然理论表达式中忽略了结构的阻尼项，但通过参数化研究发现，当两结构的阻尼比相同或者不同时，阻尼器的优化参数值都不变，并且都与阻尼器优化参数理论值非常一致。

图2 结构振动能量均方差随Kelvin型阻尼器刚度系数变化曲线(ξ1= ξ2=0.02)Fig.2 Vibration energy changes with the sum of stiffness of visco-elastic damper(ξ1= ξ2=0.02)

图3 结构振动能量均方差随Maxwell型阻尼器松弛时间变化曲线(ξ1=0.05，ξ2=0.02)Fig.3 Vibration energy changes with the sum of relaxation of viscous fluid damper(ξ1=0.05，ξ2=0.02)

图4 结构振动能量均方差随Kelvin(Maxwell)型阻尼器阻尼系数变化曲线Fig.4 Vibration energy changes with the sum of damping coefficients of dampers

3.2 场地条件的变化对阻尼器优化参数的影响

地震激励模型中的ωg与ζg分别代表场地土的卓越角频率和阻尼比，取不同的数值可代表不同的场地土类型。为了研究场地条件的变化对阻尼器优化参数的影响，采用如下4种地震激励:

场地1:ωg=15.6 rad/s，ζg=0.60，S0=4.65 ×10-4m2/rad·s3，

场地2:ωg=9.55 rad/s，ζg=0.50，S0=4.65 ×10-4m2/rad·s3，

场地3:ωg=5.18 rad/s，ζg=0.40，S0=4.65 ×10-4m2/rad·s3，

场地4:ωg=3.14 rad/s，ζg=0.30，S0=4.65 ×10-4m2/rad·s3，

其中，场地1和场地2分别代表坚硬土质和中硬土质;场地3和场地4代表软弱土质。可发现，所选场地的卓越角频率分别对应于结构1和结构2的第一阶和第二阶自振频率。由于在计算阻尼器优化参数理论值时，仅考虑了结构的第一阶自振频率，因此本文选取这四种场地土类型来研究理论表达式的适用性。

根据前一小节的研究成果，结构的阻尼比变化对阻尼器的优化参数值影响很小，在本节中仅研究两结构阻尼比均为0.02的情况。采用参数化研究方法，得出不同场地条件下，结构振动能量均方差随Kelvin型阻尼器的刚度以及Maxwell型阻尼器的松弛时间的变化曲线同图2和图3，因此优化的kd和λ均为0。图5为结构振动能量均方差随Kelvin(Maxwell)型阻尼器的阻尼cd(c0)的变化曲线。从图中可以看出，当场地土的卓越角频率改变时，阻尼器的优化阻尼变化不大，与理论值吻合良好。该结论更进一步的验证了基于两结构的第一阶自振频率和总质量来得到阻尼器优化参数的正确性。

3.3 强震作用下阻尼器优化参数的取值

本小节研究结构进入弹塑性状态时阻尼器优化参数的取值，结构滞回特性采用Bouc-Wen模型来模拟，结构各层极限屈服位移dji取为 2.5 cm，αji取为 0.1，滞回控制参数A=1、β =1.95、γ =-0.75、η =1。分别从频域和时域两个方面进行分析，频域分析采用等效线性化方法，各场地类型的地面运动激励强度S0取为4.65×10-2m2/rad·s3。在进行时域分析时共采用三条地震波，分别是 EI Centro波、Northridge波和 Kobe波，并将地震加速度峰值均调幅为0.4 g。

图5 结构振动能量均方差随Kelvin(Maxwell)型阻尼器阻尼系数变化曲线Fig.5 Vibration energy changes with the sum of damping coefficients of dampers

图6 结构1底层速度均方差随Kelvin型阻尼器刚度系数和阻尼系数的变化曲线Fig.6 Velocity of first floor of structure 1 changes with the sum of kdand cd

图7 结构相对振动能量随Kelvin(Maxwell)型阻尼器阻尼系数的变化曲线Fig.7 Vibration energy changes with the sum of damping coefficients of dampers

图6(a)为对应于不同场地类型的结构1底层速度均方差随Kelvin型阻尼器的刚度kd的变化曲线，与结构处于线弹性状态时的变化趋势是一致的，优化刚度为0。图6(b)为结构1底层速度均方差随Kelvin型阻尼器的阻尼cd的变化曲线，优化阻尼约为5.5×107N·s/m，这与线弹性状态下采用理论表达式计算得到的优化值非常接近。

根据频域分析结果，Kelvin型阻尼器的优化刚度kd与Maxwell型阻尼器的松弛时间λ均为0，两种类型的阻尼器均变为经典的线性流体阻尼器。图7为采用时程分析方法计算得到的在三种地震波激励下，结构的相对振动能量随Kelvin(Maxwell)型阻尼器阻尼cd(c0)的变化曲线。从图中可以看出，对应于控制目标1，优化阻尼分别为6.0 ×107N·s/m、5.5 ×107N·s/m和4.0×107N·s/m;对应于控制目标2，优化阻尼分别为6.5×107N·s/m、5.0 ×107N·s/m 和 4.0 ×107N·s/m。可得出在不同地震波作用下，阻尼器的优化阻尼相差不大，并且都与理论值4.80×107N·s/m和4.43×107N·s/m比较接近。以EI Centro波为例，没有阻尼器控制时结构1和两结构总的相对振动能量分别为和添加阻尼器进行控制后，相对振动能量分别降低到1.62 ×107J和2.19 ×107J，减小百分比分别达到34.9%和 41.0%。

4 结论

本文对相邻结构间连接的Kelvin型粘弹性阻尼器和Maxwell型粘滞流体阻尼器优化参数理论表达式的适用性作了详细的研究，并得出如下结论:

(1)结构阻尼比的变化对阻尼器优化参数值影响不大，当两结构的阻尼比相同或者不同时，阻尼器的优化参数值都不变，并且都与理论值非常一致。

(2)不同场地条件下阻尼器的优化参数值均与理论值吻合良好，更进一步的验证了基于两结构的第一阶自振频率和总质量来得到阻尼器优化参数的正确性。

(3)结构进入弹塑性状态时的阻尼器优化参数取值与结构在线弹性状态的取值相差不大，均与理论值比较接近。并且采用此优化参数值，对弹塑性状态下结构的响应也能起到很好的控制效果。该结论非常有利于阻尼器的优化参数理论表达式的应用。

［1］赵建伟，邹立华，方雷庆.考虑相邻建筑物碰撞的基础隔震结构的地震反应分析［J］.振动与冲击，2010，29(5):215-219.

ZHAO Jian-wei， ZOU Li-hua， FANG Lei-qing. Seismic response analysisofbase-isolated structuresconsidering pounding of adjacent buildings［J］.Journal of Vibration and Shock，2010，29(5):215-219.

［2］ Lu X L，Gong Z G，Weng D G，et al.The application of a new structural control concept for tall building with large podium structure ［J］. Engineering Structures， 2007，29(8):1833-1844.

［3］Zhang W S，Xu Y L.Dynamic characteristics and seismic response of adjacent buildings linked by discrete dampers［J］.Earthquake Engineering and Structural Dynamics，1999，28(10):1163-1185.

［4］ Zhang W S，Xu Y L.Vibration analysis of two buildings linked by Maxwell model-defined fluid dampers［J］.Journal of Sound and Vibration.2000，233(5):775-796.

［5］ Zhu H P，Iemura H.A study of response control on the passive coupling element between two parallel structures［J］.International Journal of Structural Engineering and Mechanics，2000，9(4):383-396.

［6］Zhu H P，Xu Y L.Optimum parameters of Maxwell modeldefined dampers used to link adjacent structures［J］.Journal of Sound and Vibration，2005，279(1-2):253-274.

［7］朱宏平，杨紫健，唐家祥.利用连接装置控制两相邻结构的地震动响应［J］.振动工程学报，2003，16(1):56-61.

ZHU Hong-ping，YANG Ze-jian，TANG Jia-xiang.Control of the seismic response of two adjacent structures using a damped link［J］.Journal of Vibration Engineering，2003，16(1):56-61.

［8］Bhaskararao A V，Jangid R S.Optimum viscous damper for connecting adjacent SDOF structures for harmonic and stationary white-noise random excitations［J］.Earthquake Engineering and Structural Dynamics，2007，36(4):563-571.

［9］Zhu H P，Ge D D，Huang X.Optimum connecting dampers to reduce the seismic responses of parallel structures［J］.Journal of Sound and Vibration，2011，330(9):1931-1949.

［10］ Wen Y K.Method for random vibration of hysteretic systems［J］.Journal of the Engineering Mechanics Division，1976，102(EM2):249–263.

［11］林家浩，张亚辉.随机振动的虚拟激励法［M］.北京:科学出版社，2004.