热声激励下金属薄壁结构的随机疲劳寿命估算
沙云东,魏 静,高志军,钟皓杰
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
超高音速飞行器结构在工作时承受复杂的机械力载荷、气动力载荷、热载荷和高温强噪声载荷[1]。其中,在高温强噪声载荷作用下,薄壁结构表现出复杂的大挠度非线性响应,热载荷引起的热应力可以引发结构热屈曲,强声载荷可使屈曲前结构围绕初始平衡位置做大幅值振动,使得屈曲后结构在多个屈曲后平衡位置之间做剧烈跳动,即跳变运动,或围绕一个屈曲后平衡位置振动[2]。热声载荷作用下出现快速的交变作用应力,薄壁结构会发生裂纹的萌发、扩展甚至失效。因此高温强噪声作用下结构的响应分析和疲劳寿命估算已经成为先进飞行器设计的关键问题。
热声载荷作用下,结构跳变响应时位移近似服从Fokker-Plank分布[3-4],无法确定应力峰值概率密度函数,因此无法直接使用基于高斯分布或者瑞利分布假设的功率谱密度法、概率密度法[5-7]等频域方法。时域方法直接针对结构的载荷时间历程,适用于任何概率分布的平稳或非平稳响应的寿命估算。本文采用时域方法直接对结构的应力时间历程进行采样和雨流循环计数。由于围绕一个屈曲后平衡位置的非线性振动具有极高的应力循环均值,无法直接使用一般的对称循环试验得到的零平均应力的S-N曲线进行疲劳寿命估算,因此采用Morrow TFS、SWT平均应力模型获得零平均应力的等效循环,结合Palmgren-Miner线性损伤理论进行损伤估算。以四边简支铝合金板为研究对象,计算了在不同热声载荷下的结构的动态响应和疲劳寿命,并分析了结构疲劳寿命的变化规律。
1 平均应力模型
结构大挠度非线性振动时,薄膜应力的出现使得应力循环不对称,应力均值不为零。试验结果表明等幅值时,平均应力的增大可使疲劳寿命下降[8]。本文在基本的应力寿命关系模型基础上,给出了考虑平均应力影响的寿命估算模型。
疲劳循环可以循环最大值Smax,循环最小值Smin也可以使用循环幅值和均值表示。应力循环幅值为:

应力循环均值为:


对称循环载荷作用下,使用Basquin方程表示的应力-寿命基本关系为:

由式(4)确定疲劳寿命:

本文采用 Baseline(不考虑平均应力)、Morrow TFS、SWT三种模型进行疲劳寿命分析,按等损伤原则将非零应力均值循环转换为零应力均值的循环。
Morrow TFS平均应力公式:
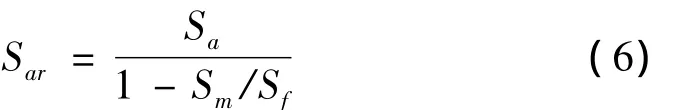
式中:Sf表示真实断裂强度。
SWT平均应力公式:

其他的平均应力模型还包括 Walker模型、修正的Walker模型、MMPDS模型等。其中Walker模型的精度较高,但是需要通过非零均值试验数据的获得拟合参数[8]。试验数据的匮乏限制了它们的使用。
2 累积损伤理论
Miner线性损伤累积理论,忽略了加载次序及载荷间相互作用的影响,由于形式简单,而广泛应用于实际工程中。线性疲劳累积损伤表示为:

式中:Ni表示在第i级等幅值应力载荷下的工作循环次数;(Nf)i为第i级等幅值应力载荷下,构件发生破坏时的循环数。
随机响应的损伤期望可以使用数学期望和概率密度表示为:
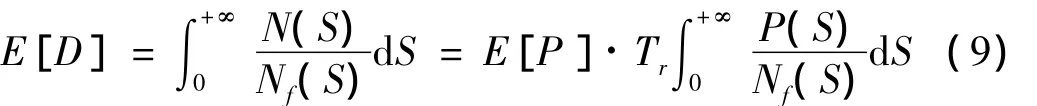
式中:Ni=N(S)=E[P]·T·P(S);S为应力幅值;P(S)为应力峰值概率密度函数;E[P]为单位时间内的峰值期望;Tr为响应信号时长。
窄带随机信号的峰值概率密度服从瑞利分布,宽带信号的峰值概率密度是高斯分布与瑞利分布的不同组合,两者可以通过经验公式获得其表达式。本文中热声载荷作用下结构应力响应幅值的分布律目前还没有明确的表达式,因此通过雨流循环计数获得应力循环的联合概率密度函数的数值估计。
假设第k次雨流循环(RFC)的局部极大值和极小值分别为Smax和Smin,时间Tr内的总损伤为:

式中:P(Smin,Smax)为应力循环极小值和极大值的联合概率密度函数;Nf(Smin,Smax)为应力循环作用下的疲劳寿命,取决于平均应力模型的选择。使用有限时长信号的雨流循环矩阵(RFM)估算P(Smin,Smax):

式中:NRF为雨流循环次数。
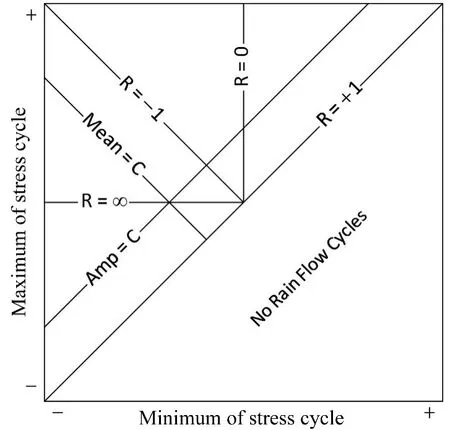
图1 雨流循环矩阵示意图Fig.1 RFM
本文中利用MATLAB工具箱WAFO[9]获得RFM。RFC可以使用三维图象表示。如图1平面直方图所示,在RFM中,X轴和Y轴分别为循环对的极小值和极大值,循环计数结果对应RFM中一点。将RFM离散为n×n块后,(i,j)块对应Z轴的循环对数目即RFM(Si,Sj)的数值。由于循环对中极小值必然小于极大值,所以循环只分布在平面图的左上区域。循环对于R=1对角线距离越远,循环的幅值越大;循环对于R=-1对角线的距离越远,循环的平均应力越大。
对于有限时长响应信号Tr:E[P]≈NRF/Tr;
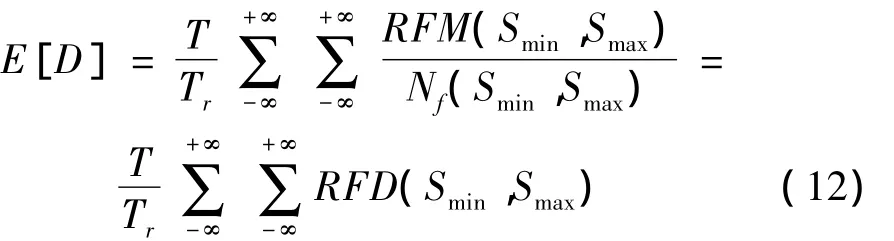
式中:RFD(Smin,Smax)为2维雨流循环损伤矩阵。当E[D]=1,结构发生疲劳失效。疲劳寿命时间为:

3 应用实例
将研究的疲劳寿命估算方法,应用于四边简支铝合金板(2024-T3)。假定在拉、压载荷下的屈服应力不变,材料特性不随温度变化。结构尺寸为a=0.2 m,b=0.2 m,h=0.005 m,密度为 ρ=2 723 kg/m3,弹性模量E=73.11 GPa,泊松比为 μ=0.33,热膨胀系数为 α=22.32 ×10-61/K。
结构的模态频率和临界屈曲温度,见表1和2。
采用Basquin公式拟合的2024 T3铝合金的S-N曲线表达式为:S6.4935n=1.289 8 ×1021。
Morrow TFS模型中,2024 T3铝合金的材料常数为[10]:Sf=610 MPa,σ'f=1 602 MPa,b=0.154。

表1 四边简支铝合金板的模态频率Tab.1 The modal frequencies of simply-supported aluminum plate[Hz]

表2 四边简支铝合金板的临界屈曲温度Tab.2 The critical buckling temperatures of simply-supported aluminum plate[°C]
为方便表示,采用热屈曲系数S=T/TC表示温度,T为实际温度,TC为屈曲温度。

图2 位移时间历程(UZ,0,160)Fig.2 Time history(UZ,0,160)
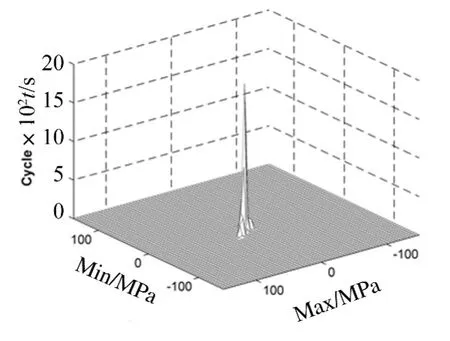
图3 雨流循环矩阵(SX,0,160)Fig.3 RFM(SX,0,160)
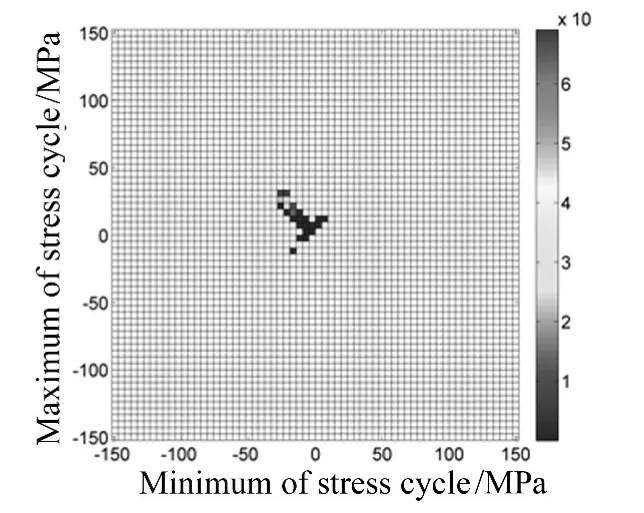
图4 雨流循环损伤矩阵(SX,0,160)Fig.4 RFD(SX,0,160)

图5 位移时间历程(UZ,1,160)Fig.5 Time history(UZ,1,160)
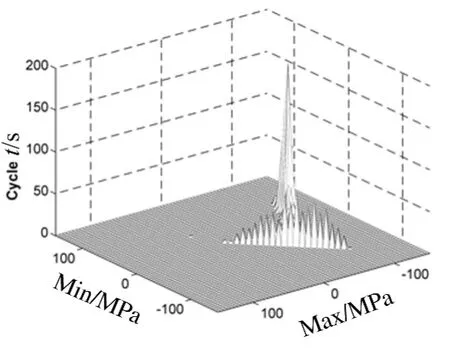
图6 雨流循环矩阵(SX,1,160)Fig.6 RFM(SX,1,160)

图7 雨流循环损伤矩阵(SX,1,160)Fig.7 RFD(SX,1,160)
3.1 热声载荷的模拟
选用有限带宽高斯白噪声作为声载荷,声压级范围为140 dB到170 dB,间隔10 dB。截止频率为1 500 Hz,覆盖前3阶结构模态。噪声信号的时长为4.5 s。声载荷在板面均匀分布,即垂直入射加载。热载荷在空间均匀分布,屈曲系数范围为0到4,间隔0.2。
文中使用(SX,0,160),(UZ,0,160)分别表示 S=0、SPL=160 dB时的X向应力和Z向位移。
3.2 薄壁铝合金板在热声载荷下的响应和疲劳寿命
采用有限元软件分析得到铝合金板在不同热声载荷下的位移和应力响应时间历程。热声载荷下结构典型的运动形式包括,常温时围绕初始位置的线性随机振动,如图2所示,屈曲前围绕初始位置的非线性随机振动,如图5所示,屈曲后两个平衡位置之间的跳变响应,如图8所示,屈曲后围绕一个屈曲后平衡位置的非线性随机振动,如图11所示。
简支铝板中点在不同声压级和屈曲系数下的X向应力有效值如图14所示。常温时,应力有效值最低。随着S的增加,屈曲前结构刚度降低,应力RMS随着S线性增加。屈曲后结构发生跳变运动,在频繁跳变区域,应力RMS随着S增加。温度继续升高,跳变频率下降,有效值下降,当结构停止跳变后,应力有效值重新进入上升区域。
中点在不同屈曲系数下的X向应力的雨流循环矩阵如图 3、6、9、12 所示。
常温时,结构围绕初始平衡位置振动,应力循环的均值近似为零,图3中的应力循环块分布呈短柱状。
随着温度的增加,压缩热应力作用使结构的刚度下降,响应水平提高,应力循环均值下降(绝对值增大)。与常温相比,临界屈曲时的应力循环幅值明显增加,循环块整体向左下侧移动,同时循环块扩散,出现很多小幅值循环,表明此时的响应为宽带过程,如图6所示。屈曲后结构频繁跳变时,应力循环块分布总体呈三角状,分为3块。左上区域对应纯跳变运动,应力循环的幅值大、均值绝对值小。左下区域对应围绕下凹平衡位置的振动,应力循环的均值绝对值最大,这是由于中点围绕下凹平衡位置振动时,压缩热应力叠加了压缩弯曲应力。右上区域对应围绕上凸平衡位置的振动,应力循环的均值较小,这是由于铝板中点围绕上凸平衡位置振动时,压缩热应力叠加了拉伸弯曲应力,如图9所示。
当温度足够高时,结构停止跳变运动,围绕一个屈曲后平衡位置振动。相应地,雨流循环矩阵图的左上角循环块消失,左下角和右上角的循环块只存其一,如图12所示。温度越高,应力循环的幅值越小,均值越大,循环块逐渐向右上方向移动。由于同等压缩载荷造成的损伤要比拉伸载荷小30%。因此后文重点考虑了中点处于拉伸应力状态时的响应结果,进行保守寿命估算[11]。
采用Morrow TFS和SWT平均应力模型对雨流循环进行等效处理,采用线性损伤累积理论进行损伤计算,得到与雨流循环矩阵对应的二维雨流循环损伤矩阵 RFD,如图 4、7、10、13 所示。由图 10,13 可以清晰地看出,虽然左上角的大幅值应力循环次数远比右下角的小幅值应力循环次数少,但造成的循环损伤却非常大。
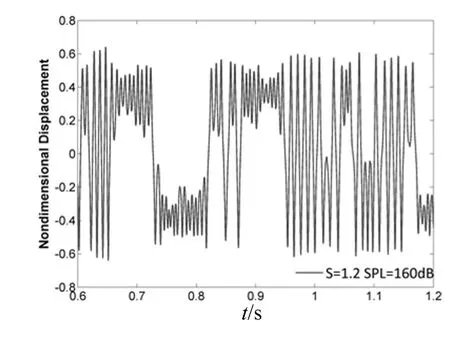
图8 位移时间历程(UZ,1.2,160)Fig.8 Time history(UZ,1.2,160)

图9 雨流循环矩阵(SX,1.2,160)Fig.9 RFM(SX,1.2,160)
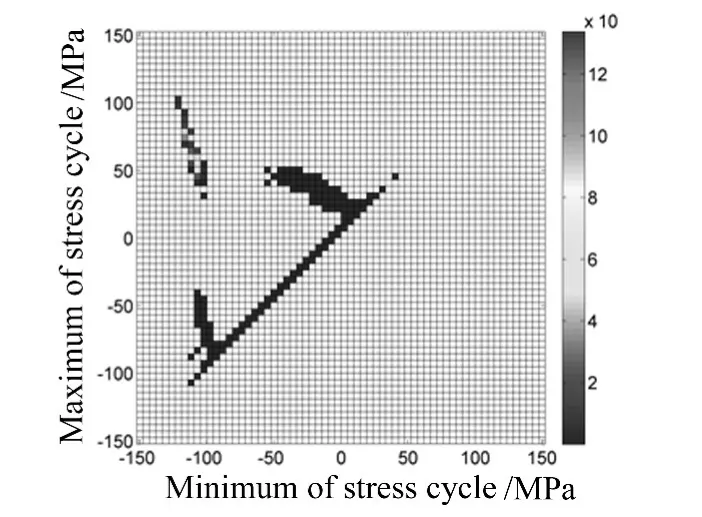
图10 雨流循环损伤矩阵(SX,1.2,160)Fig.10 RFD(SX,1.2,160)

图11 位移时间历程(UZ,1.8,160)Fig.11 Time history(UZ,1.8,160)
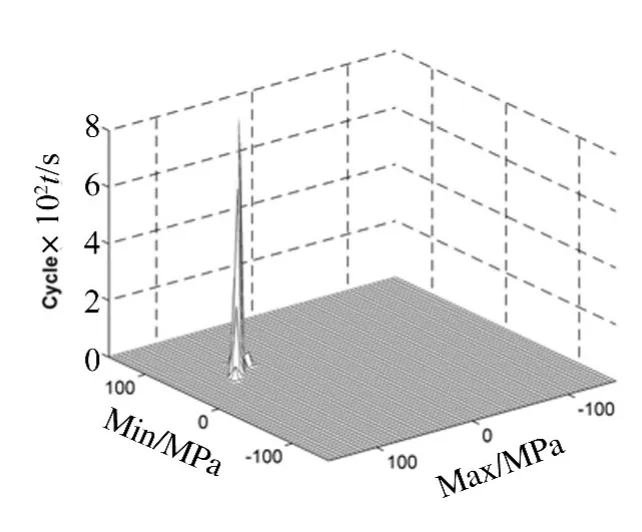
图12 雨流循环矩阵(SX,1.8,160)Fig.12 RFM(SX,1.8,160)
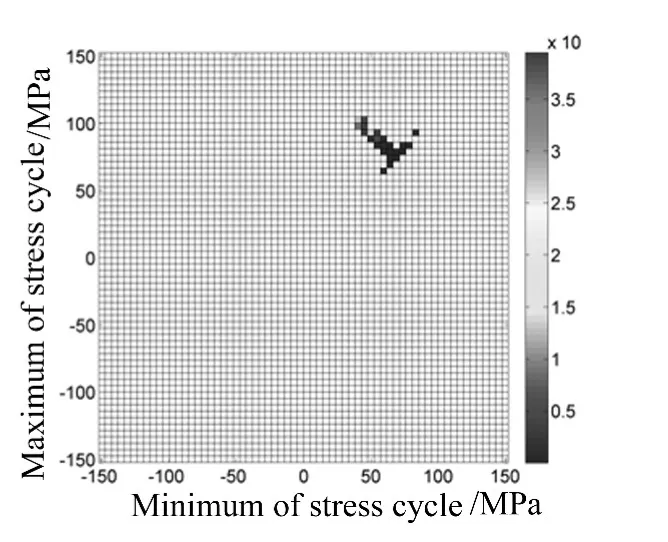
图13 雨流循环损伤矩阵(SX,1.8,160)Fig.13 RFD(SX,1.8,160)
屈曲前,结构承受压缩平均应力,如图3,4,6,7所示。三种平均应力模型估算的差别不大,Morrow TFS模型和Baseline模型的寿命基本相同,说明当前平均应力模型对压缩平均应力的影响并不敏感。屈曲后结构处于拉伸应力状态,且热平均应力较大,如图12,13所示,SWT模型和Morrow TFS模型的结果相差较大,说明不同平均应力模型对拉伸应力的敏感度差别较大,即SWT等效处理后的零均值循环幅值更大。SWT估算寿命结果更加保守。三种模型均预测频繁跳变时的结构寿命最低,并且相差不大,这是由于频繁跳变时,应力循环的幅值较大,均值较小,平均应力处理的影响很小。采用三种模型得到的寿命估算结果较高,这是由于随着温度的升高,热平均应力不断增加,当接近屈服应力时,没有考虑高低周复合疲劳,以及高温疲劳寿命曲线的影响。
声载荷对结构的作用本质上是一种空间分布的,并且具有一定频率分布特性的动态随机压力载荷,超过一定量值后,如声压级超过140 dB,便可能对结构产生较大激励,特别是当噪声的频率分布特性和结构的动态特性相近时,结构就会产生显著的应力响应。使用SWT模型计算的不同声压级下的疲劳寿命变化曲线如图16所示。随着声压级的增加,结构频繁跳变的范围扩大,因此图中的寿命最低点向右移动。温度相同时,声压级越大,应力循环的幅值越大,寿命自然越短。
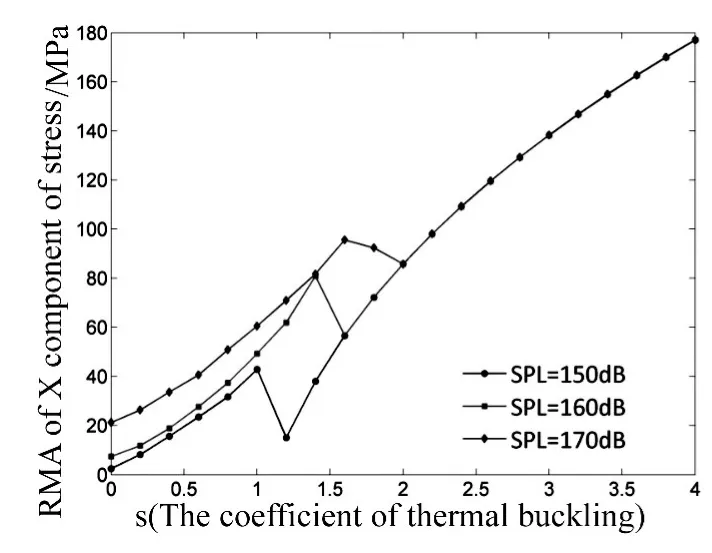
图14 X向应力RMS随着温度变化Fig.14 RMS of X component of stress at different temperature
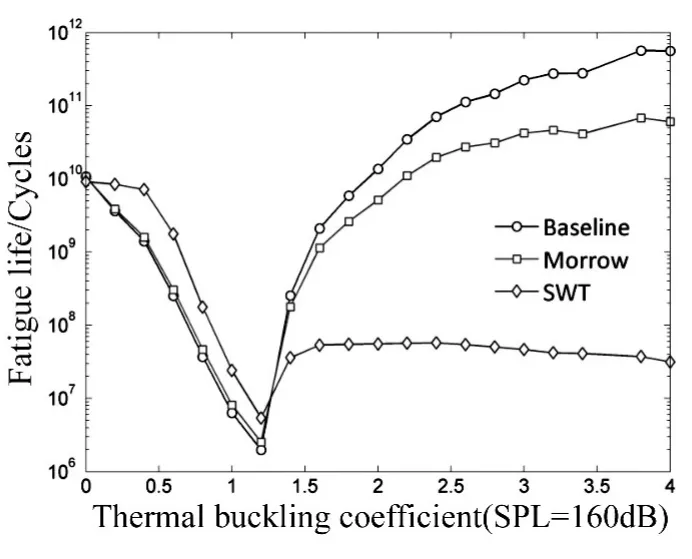
图15 不同平均应力模型的疲劳寿命Fig.15 Fatigue life of central node using different models

图16 SWT模型不同SPL的疲劳寿命Fig.16 Fatigue life at different SPLs using SWT
4 结论
(1)运用雨流循环矩阵和损伤矩阵可以直观的分析结构热声非线性响应和寿命变化规律。使用RFM可以清晰分辨出不同类型的热声响应运动。随着温度的增加,应力循环的均值绝对值逐渐增加。屈曲前应力循环的幅值逐渐增加,屈曲后结构的应力循环幅值逐渐下降。均值相同时,幅值越大损伤越大。幅值相同,均值越大损伤越大。
(2)热声载荷下,薄壁结构的非线性响应显著影响着结构的疲劳寿命。屈曲前,随着温度升高,热应力增大,寿命呈降低趋势;跳变过程中,大幅值应力循环造成的疲劳损伤使得此时的疲劳寿命达到最低点;跳变结束后,应力循环均值显著增大,幅值降低,不同平均应力模型的结果差别较大,随着温度升高,Morrow TFS模型估算得到的寿命上升,SWT模型得到的寿命缓慢下降。
(3)不同的平均应力模型对压缩应力均不敏感,因此不同平均应力模型得到屈曲前结构的寿命差别不大,但是在拉伸应力区,不同模型差别较大。结构在高温时的疲劳寿命变化规律还需要进一步的研究。
[1]吴振强,任 芳,张 伟.飞行器结构热噪声试验的研究进展[J].导弹与航天运载技术,2010,2:24-30.
WU Zhen-qiang, REN Fang, ZHANG Wei. Research advances in thermal-acoustic testing of aerocraft structures[J].Missiles and Space Vehicles,2010,2:24-30.
[2]Mei C.Nonlinear random response of composite panels in an elevated thermal environment[J]. Air Force Research Laboratory AFRL-VA-WP-TR-2000-3049, WPAFB,OH,2000.
[3] Lee J.Displacement and strain histograms of thermally buckled composite plates in random vibration[C].In AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference and Exhibit,37th.1996,AIAA:Salt Lake City,UT.
[4] Sha Y D,Gao Z J,Xue F,et al.Influence of thermal loading on the dynamic response of thin-walled structure under thermo-acoustic loading[J]. Applied Mechanics and Materials,2011,2-3:876-881.
[5]沙云东,郭小鹏,张 军.基于应力概率密度和功率谱密度法的随机声疲劳寿命预估方法研究[J].振动与冲击,2010,29(1):162-165.
SHA Yun-dong,GUO Xiao-peng,ZHANG Jun.Random sonic fatigue life prediction based on stress probability density and power spectral density method[J].Vibration and Shock,2010,29(1):162-165.
[6]沙云东,郭小鹏,廖连芳,等.随机声载荷作用下的复杂薄壁结构VonMises应力概率分布研究[J].振动与冲击,2011,30(1):137-141.
SHA Yun-dong,GUO Xiao-peng,LIAO Lian-fang,et al.Probability distribution of Von Mises stress for complex thinwalled structures undergoing random acoustic loadings[J].Vibration and Shock,2010,30(1):137-141.
[7] Sha Y D,Zhang Z,Zhao F T,et al.Estimation of random sonic fatigue life based on peak probability density of von mises stress[J].Advanced Materials Research,2011,199:913-921.
[8] Sweitzer K A,Ferguson N.Mean stress effects on random fatigue ofnonlinear structures[C]. In the twelfth international congress on sound and vibration,2005:11-14.
[9] WAFO-A Matlab toolbox for analysis of random waves and loads,Version 2.1.1[M].The WAFO Group,Lund Institute of Technology,Lund University,2000:343-350.
[10] Lukas P,Kunz L.Effect of mean stress on cyclic stresssStrain response and high cycle fatigue life[J].International Journal of Fatigue,1989,11(1):55-58.
[11] Przekop A,Rizzi S A,Sweitzer K A.An investigation of highcycle fatigue models for metallic structures exhibiting snapthrough response[J].International Journal of Fatigue,2008,30(9):1579-1598.

