考虑非局部效应的纳米梁非线性振动

刘灿昌，裘进浩，季宏丽，刘 露

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016;山东理工大学 交通与车辆工程学院，淄博 255049)

随着微、纳机电系统技术的发展，超薄纳米梁经常被用作超高精度传感器、超高频混频器等。与以往的微米梁相比，纳米梁在尺寸上进一步缩小，性能获得了极大的提高。但是，由于器件进入了纳米尺度，非局部效应影响较为显著，不可以再予以忽略［1］。

近年来，纳米结构的线性和非线性动力学研究取得较快的进展。杨晓东等［2］分析考虑非局部效应的两端简支纳米材料梁的横向非线性振动特性。考虑非局部效应的碳纳米管的线性和非线性振动得到深入研究［3-7］。宋震煜等［8］考虑纳米梁的轴向非线性伸长因素，分析了纳米梁的幅频特性和纳米梁非线性产生的物理机制。朱年勇等［9］利用数值方法求解了描述纳机电谐振器的达芬方程，研究了纳机械谐振梁的非线性行为。纳米梁的制造与测试工作取得较大进展［10-12］。

本文以弹性理论和非线性振动理论为基础，考虑纳米梁的非局部效应，从梁的轴向非线性伸长出发对纳米梁进行受力分析，建立连续体非线性物理模型。探讨了纳米谐振梁非线性特性产生的物理机制，分析非局部效应对固有频率的影响，探讨非局部效应对主共振幅频特性曲线的影响，对纳米谐振梁的振动特性进行了分析。

1 连续体模型

实验表明，传统的宏观梁甚至MEMS谐振梁通常只工作在线性区，而特征尺寸为纳米量级的谐振梁随着外部激励的逐渐增加很快就进入非线性工作区，原有的线性理论不再适用［13］。本文从弹性理论出发建立考虑纳米梁横向振动几何非线性和非局部效应的动力学方程。仅考虑细长均匀梁的横向振动，假定梁的各截面的中心主惯性轴在同一个平面内，外载荷也作用在该平面内，梁在该平面内作横向振动，梁的两端固定，其端部运动就受到限制，引起中性面伸长。对于细长纳米梁其剪切变形以及截面绕中性轴的转动惯量可以忽略。取梁的微元进行受力分析，如图1所示。在微元左侧，梁受到的垂直剪力为V，弯矩为M，P是由于横向振动导致中性面伸长而产生的张力，θ为张力与x轴的夹角。右侧为相应的受力变化。q为作用于梁上的分布力。由力的平衡条件可以得到在横向振动方向平衡方程:

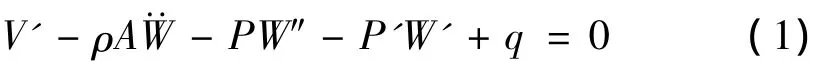
其中，W为梁横向振动幅值;ρ为梁单位长度的质量;A为梁的截面面积;()'=∂/∂X， ()″=∂2/∂X2，(··)=∂2/∂T2。由微元的力矩平衡方程，略去二阶小量后，得到:

图1 纳米梁几何非线性振动模型Fig.1 Geometrical non-linear vibrational model of nano-beam

根据非局部弹性理论，可以知道应力-应变关系为

其中，σX和εX为经典弹性理论的应力和应变，参数e0a为考虑纳米结构小尺度效应的长度量纲参数，E为材料的弹性模量。根据非局部弹性理论，可以推导出轴向张力P、弯矩M与变形之间的关系

其中，I为截面的惯性矩。

将式(5)进行二次求导运算后，再将式(1)和(2)代入(5)，考虑系统的阻尼并等效为黏性阻尼，得到

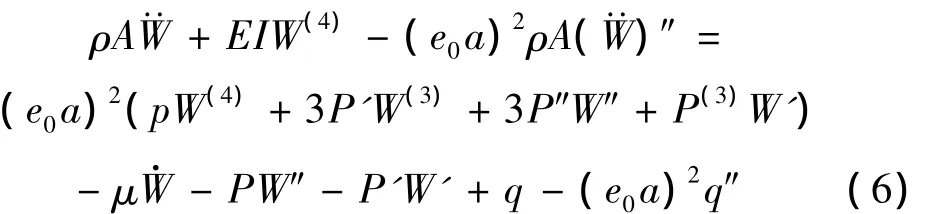
这是考虑几何非线性因素和非局部效应的两端固支纳米梁动力学方程，对其求解即可得到梁的振动特性。式中，μ是等效黏性阻尼系数。将方程无量纲化，再引入小参数ε，设激励力幅值与小参数ε同数量级，阻尼项和轴向力因素项也与小参数ε同数量级，系统的非线性振动微分方程为

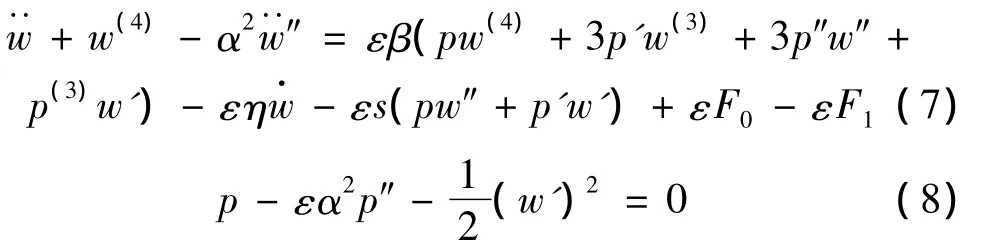
其中，

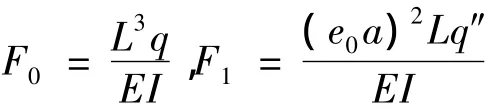
两端固支纳米梁的边界条件为:

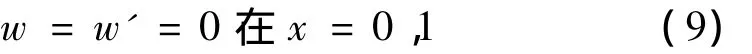
方程的解w和轴向力P可以展开为ε的幂级数形式:

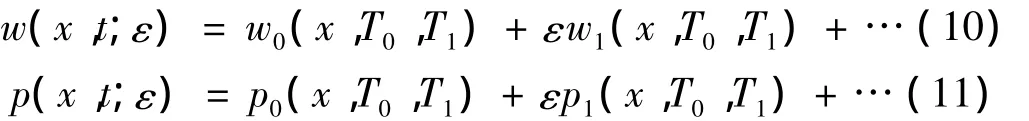
其中T0和T1分别为慢变和快变时间尺度。将方程(10)和(11)分别代入到方程(7)、(8)和边界条件(9)，令ε同幂次的项系数为零，得到以下各阶近似线性方程:

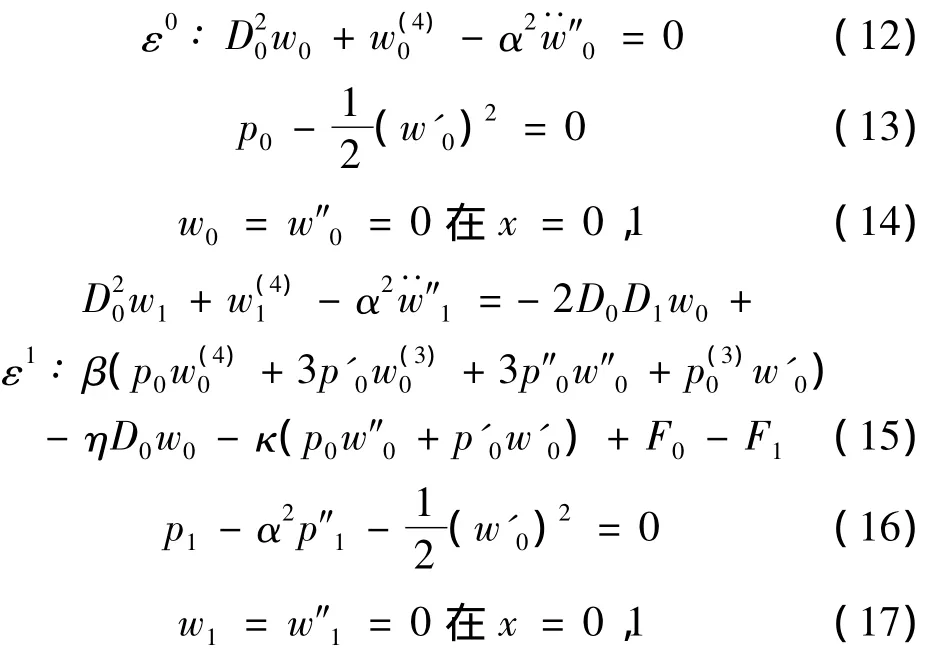
2 非局部效应纳米梁固有频率和模态函数

方程(12)的通解可以写为:

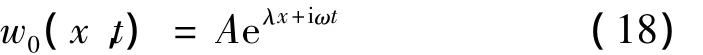
将方程(18)代入到(12)，可以得到本征方程:

方程(19)的四个本征值为:

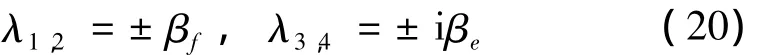
其中，

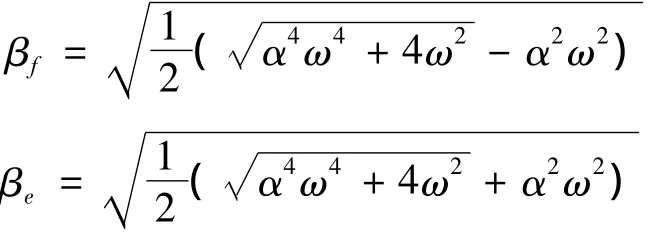
方程(12)通解的模态函数为:

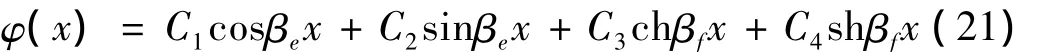
其中，Cj(j=1，2，3，4)和 ω 为待定参数，分别由梁的边界条件确定。

对于两端固支纳米梁，其边界条件为:

将(21)代入边界条件(22)，由系数非零解条件得到:

解方程即可得到固有频率解。当α为零时，方程(23)退化为不考虑非局部效应的两端固支梁的频率方程1-cosβcoshβ =0。

两端固支纳米梁各阶模态函数为:

其中:

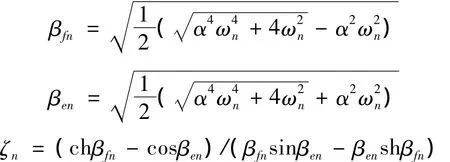
3 非局部效应纳米梁主共振分析

当激励频率Ω接近于非线性振动系统的派生系统固有频率ωn时，可发生主谐波共振。如果系统是小阻尼系统，这时很小的激励幅值F就可以激励起强烈的共振。方程(12)的解可以表示为:

将(25)代入(13)得到:

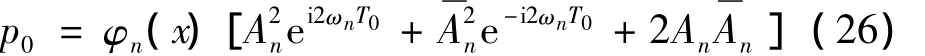
其中，φn(x)=［φ'n(x)］2。

设策动力为F0=FeiΩt。设ωn与Ω之差与小参数ε同数量级，令

将(25)和(26)代入到(15)得到:

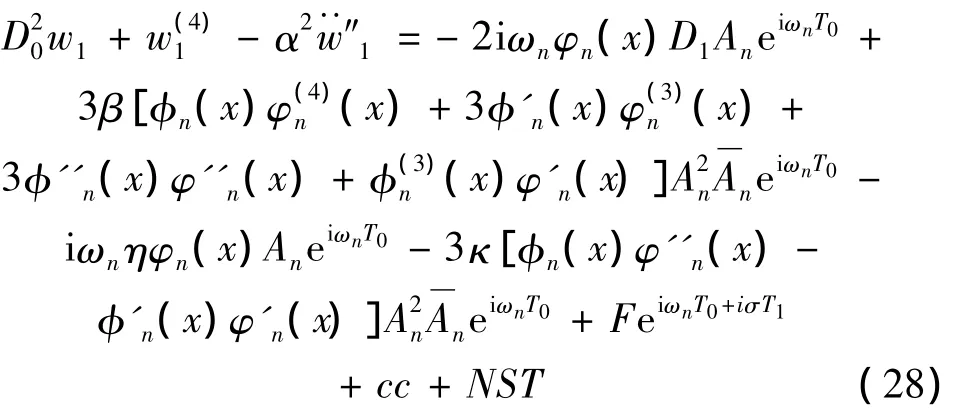
其中cc为永年项的复数共轭项，NST表示其它一般项。由两端固支纳米梁振动模态的正交性可知:

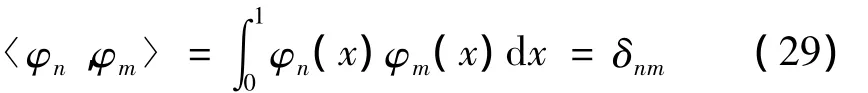
应用可解性条件，将方程(28)右端永年项乘以派生系统的模态函数并由模态的正交性可以得到:

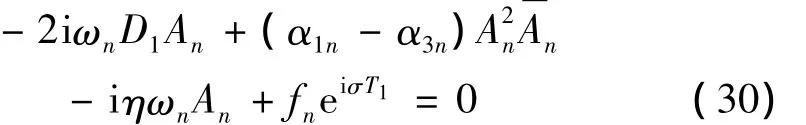
其中:

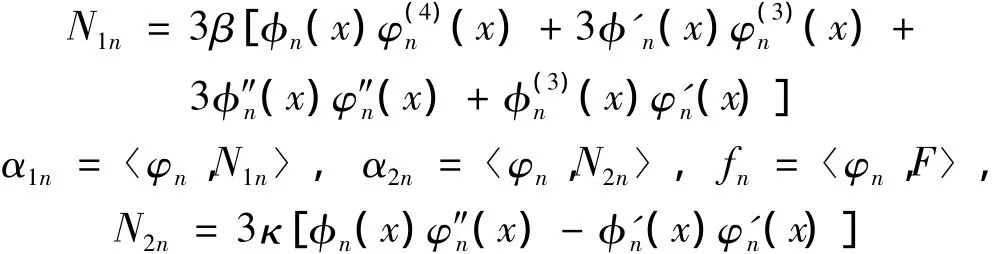
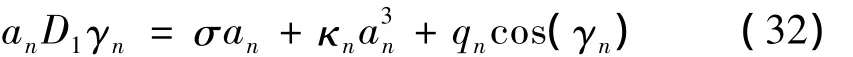
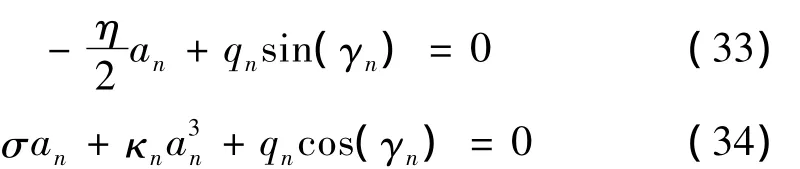
将方程(33)和(34)中的γn消掉，得到两端固支纳米梁主共振的幅频方程为:

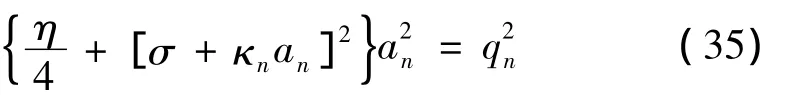
由方程(33)和(34)得到两端固支纳米梁相位为:

由方程(35)得到两端固支纳米梁主共振的峰值为:

不考虑系统阻尼，系统自由振动的方程(31)和(32)变为:

对上面两式积分，得到:

其中，an0，bn0是积分常数。由此可以得到纳米梁非线性自由振动的固有频率为:

4 算例分析

本文以两端固支纳米梁系统为仿真实例。在梁的硅基结构上面镀有一层薄金镀膜，通过外接电路施加变化电流，将该装置放于匀强磁场中，则梁系统受到随电流变化的均布磁场力作用。为了研究非局部弹性效应对纳米结构的影响，我们分别以纳米梁和微米梁作为研究对象，分析非局部弹性效应对梁力学性能的影响。纳米梁的长度、宽度和高度为150 nm×20 nm×25 nm。微米梁的长度、宽度和高度为15 μm×2 μm × 2.5 μm。两种梁的弹性模量为170 GPa，密度为 2 330 kg/m3，系统的阻尼比为 0.3。

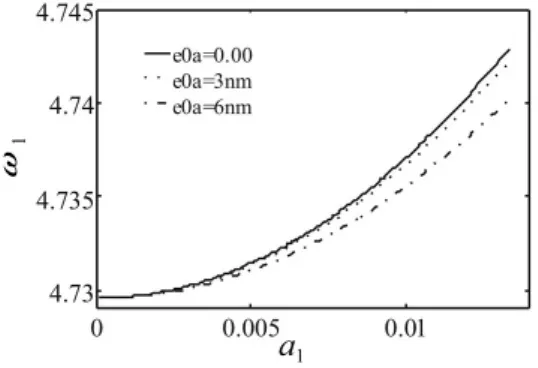
图2 纳米梁非局部效应及振幅对一阶固有频率影响Fig.2 Effect of the nonlocal elasticity and amplitude to the first natural frequency for nano-beam.

通过数值计算方法计算式(23)得到考虑非局部效应的纳米梁前两阶固有频率。数值结果见图2-图3。由图可见，随着非局部效应系数数值的变大，两端固支纳米梁固有频率要减小，考虑非局部效应后材料刚度比不考虑该效应的要小。由图中还可以看出，非局部效应系数对两端固支纳米梁高阶固有频率的影响更为明显。由图4-图5我们发现，对于不同的非局部效应系数数值，两端固支微米梁固有频率几乎没有变化，这说明非局部弹性效应对微米梁影响较小。可见，随着结构尺寸的减小，非局部弹性效应的影响逐步变大，特别是到了纳米尺度，其影响就不能再予以忽略。

由式(35)可以得到两端固支纳米梁的一阶主谐波共振响应的幅频图(如图6所示)。由图可以看出，不考虑系统的非局部效应或者非局部效应系数较小时，两端固支纳米梁存在分叉和跳跃等非线性现象，幅频关系存在着多值性，但是随着非局部效应系数的增大，图像峰值右移，分叉现象消失，说明非局部效应的存在影响主谐波共振的幅频关系。因而研究两端固支纳米梁振动特性时需要考虑非局部效应的影响。

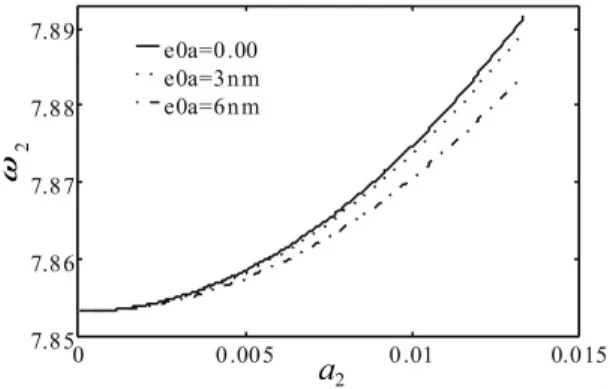
图3 纳米梁非局部效应及振幅对二阶固有频率影响Fig.3 Effect of the nonlocal elasticity and amplitude to the second natural frequency for nano-beam

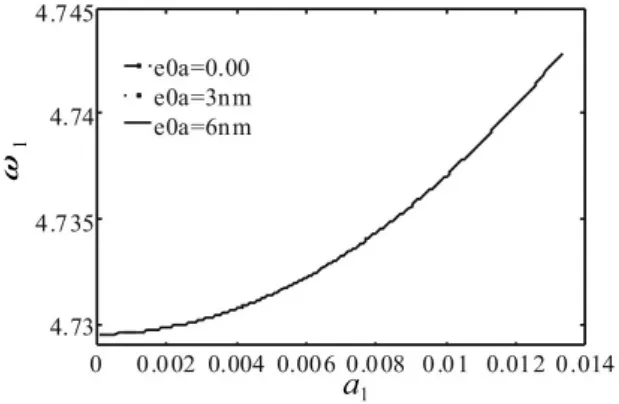
图4 微米梁非局部效应及振幅对一阶固有频率影响Fig.4 Effect of the nonlocal elasticity and amplitude to the first natural frequency for mecron-beam

图5 微米梁非局部效应及振幅对二阶固有频率影响Fig.5 Effect of the nonlocal elasticity and amplitude to the second natural frequency for mecron-beam

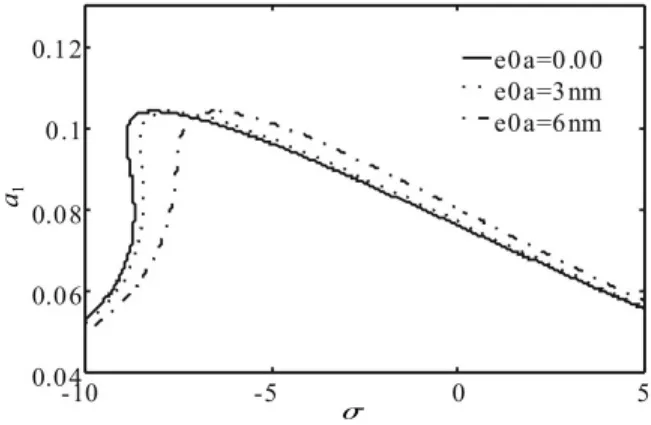
图6 纳米梁幅频响应Fig.6 Response of frequency-amplitude for nano-beam

5 结论

本文以弹性理论和非线性振动理论为基础，建立考虑非局部效应和轴向非线性伸长的两端固支纳米梁物理模型。探讨了两端固支纳米梁非线性特性产生的物理机制，研究发现由于非局部效应存在，纳米梁的固有频率比不考虑非局部效应的要小;非局部效应对高阶固有频率的影响更为显著;非局部效应的存在影响主谐波共振的幅频关系。

［1］Eringen A C.On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves［J］.Journal of Applied Physics，1983，54(9):4703-4710.

［2］杨晓东，林志华.利用多尺度方法分析基于非局部效应纳米梁的非线性振动［J］.中国科学(技术科学)，2009，40(2):152-156.

YANG Xiao-dong， LIN Zhi-hua.Nonlinear vibrations of nano-beams accounting for nonlocal effect using a multiple scale method［J］.Scientia Sinica(Technologica)，2009，40(2):152-156.

［3］Wang C M，Kitipornchai S，Lim C W.Beam bending solutions based on nonlocal Timoshenko beam theory［J］.Journal ofEngineeringMechanics， 134(6)， 2008:475 481.

［4］ Ke L L，Xiang Y，Yang J.Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory［J］. ComputationalMaterials Science，2009，47:409-417.

［5］ Yang J，Ke L L，Kitipornchai S.Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory［J］.Physica E ，2010，42:1727-1735.

［6］Pradhan S C，Murmu T.Application of nonlocal elasticity and DQM in the flapwise bending vibration ofa rotating nanocantilever［J］.Physica E，2010，42:1944-1949.

［7］Wang C M，Zhang Y Y，Kitipornchai S.Vibration of initially stressed micro and nano-beams［J］.International Journal of Structural Stability and Dynamics，2007，7(4):555-570.

［8］宋震煜，于 虹.纳米梁非线性振动的动力学分析［J］.微纳电子技术，2006(3):145-149.

SONG Zhen-yu，YU Hong.Dynamic analysis for nonlinear vibration of nano-beam［J］.Micronanoelectronic Technology，2006(3):145-149.

［9］朱年勇，于 虹，黄庆安.纳机械谐振器的非线性特性分析［J］.电子器件，2005，28(1):35-37.ZHU Nian-yong，YU Hong，HUANG Qing-an.Analysis of nonlinear characteristic of nanomechanical resonators［J］.Chinese Journal of Electron Devices，2005，28(1):35-37.

［10］夏晓媛，李昕欣，王跃林.超薄硅纳米谐振梁的制作及谐振特性的测量［J］.纳米技术与精密工程，2008，6(1):1-4.

XIA Xiao-Yuan，LI Xin-xin，WANG Xue-Lin.Fabrication and detection of ultrathin silicon nano-beam resonator［J］.Nanotechnology and Precision Engineering.2008，6(1):1-4.

［11］徐临燕，栗大超，胡小唐，等.基于原子力显微镜的纳米梁杨氏模量的测量［J］.天津大学学报，2007，40(7):816-820.

XU Lin-yan，LI Da-chao，HU Xiao-tang，et al.Measurement of Young’s modulus of nanobeam based on AFM［J］.Journal of Tianjin University，2007，40(7):816-820.

［12］陈会军，范 炜，张大成.铝纳米梁的电学特性测试［J］.纳米技术与精密工程，2008，6(1):5-8.

CHEN Hui-jun，FAN Wei，ZHANG Da-cheng.Electrical characteristics testing of aluminum nano-Beams［J］.Nanotechnology and Precision Engineering，2008，6(1):5-8.

［13］Evoy S.Carr D W.et al.Nanofabrication and electron static operation of single-crystal silicon paddle oscillators［J］.Journal of Applied Physics，1999，86:6072-607.