分子动力学仿真过程中硅晶体位错模型的构建
郭晓光 张 亮 金洙吉 郭东明
大连理工大学精密与特种加工教育部重点实验室,大连,116021
0 引言
目前,机械加工的材料即使经过化学机械抛光,仍然或多或少存在一些空位、间隙原子、位错等缺陷。材料的性能在很大程度上取决于其内部的缺陷,其中,位错缺陷对半导体材料的磁学、光学、电学、力学性能有着重要的影响。1934年,Taylor[1]提出了位错模型,解释了材料的实际强度低于理论强度的原因。Peierls[2]采用了切割粘合方法,构造了位错芯结构,研究了位错运动。Blumenau等[3]研究了螺旋位错,分析了金刚石结构晶体的塑性变形。随着计算机技术的发展,分子动力学技术被广泛应用。而在机械加工领域,分子动力学仿真研究的对象几乎都是无缺陷的理想晶体,没有考虑材料实际存在的微小缺陷,也没有涉及复杂的物理化学过程[4-7]。
本文通过对位错晶格理论的研究,分析了硅晶体不同类型位错结构的形成过程,构建了硅晶体含有60°滑移位错的模型和含有螺旋位错的模型,并应用含有螺旋位错模型进行了分子动力学仿真计算,研究了包含螺旋位错的硅晶体纳米级磨削机理。
1 位错的类型和理想硅晶体结构分析
1.1 位错的类型
当晶体中的一部分区域发生一个或多个原子的滑移,另一部分区域不滑移时,远离已滑移区的原子仍为完整晶格排布,两者边界处的原子会发生严重“错配”,这个原子错配的过渡区称为位错。位错可以分为刃位错、螺旋位错和混合位错三种类型。

图1 刃位错
刃位错是晶体在外切应力作用下,以一个面为滑移面,周围原子发生滑移的位错形式。晶体在滑移面两侧形成新的原子结构,如图1所示。刃位错是在硅片加工过程中,硅片受到磨粒的挤压作用,局部受力不均,导致晶体内部一个晶面发生滑移。在硅片磨削过程中,刃位错是一种比较常见的结构变化。
螺旋位错是在外切应力作用下,一端晶体上下区在滑移面发生了一个原子间距的切变,如图2所示。螺旋位错区的原子排布呈轴对称,所有与位错线相垂直的晶面将由原来的平面变成以位错线为中心轴的螺旋面。

图2 螺旋位错
混合位错晶体中,已滑移区与未滑移区的边界线(位错线)既不平行也不垂直于滑移方向,即滑移矢量与位错线成任意角度,这种晶体缺陷称为混合型位错,如图3所示。
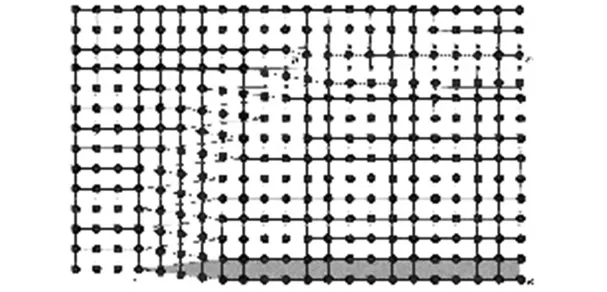
图3 混合位错
在材料的实际加工过程中,材料往往受到不均匀的外力作用。不均匀的受力使被加工的硅晶体内部部分发生滑移,同时会在晶体内部形成螺旋位错芯。
1.2 理想硅晶体的结构分析
图4所示为理想硅晶体的晶体结构,单晶硅晶体是具有金刚石结构的晶体,是典型的立方结构晶体。

图4 理想硅晶体结构
硅晶体中的位错与面心立方晶体中位错的形式比较相似[8]。本文采用类似方式进行位错结构的构建。在硅晶体晶胞结构中有着两个类似于面心立方晶体的结构,这种结构是在体对角线方向平移得到的,长度为硅晶体体对角线长度的1/4。面心立方晶体中主要的滑移面为{1 1 1}面,滑移方向为〈1 1 0〉方向,伯格斯矢量为〈1 1 0〉/2。在{1 1 1}滑移面内相对位移为〈2 1 1〉/6处存在一个能量非常低的层错。在较低的层错处,可以对全位错进行矢量分离。硅晶体同样具有这些性质,但不同之处在于金刚石结构具有两种不同的{1 1 1}面。其中的一种{1 1 1}面位于两个不同性质的密排面之间,被称作 Glide set;另一种 {1 1 1}面位于垂直{1 1 1}面的键连接的两个密排面之间,被称作Shuffle set,如图5所示。这两种不同的失配面形成了不同的位错形式:Glide位错和Shuffle位错。
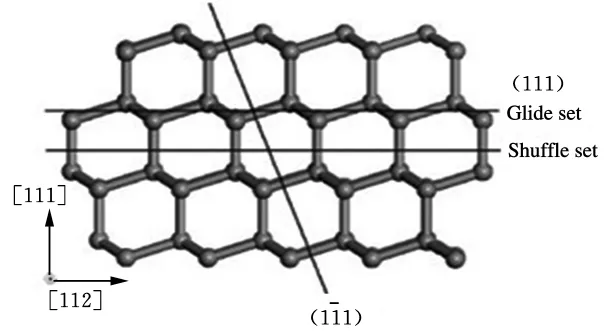
图5 硅晶体中的Glide set和Shuffle set
2 硅晶体60°滑动位错和螺旋位错模型的构建
2.1 硅晶体60°滑移位错模型
根据硅晶体的结构,基于位错晶格理论构建含有60°滑移位错初始模型[9],采用偶极子建立两个位错区域。参考应用Parrinello-Rahman方法给模型施加剪应力使2个偶极子分别在60°方向发生位错滑移。同时保证元胞中的2个60°位错芯的柏氏矢量方向相反,在整个工件中两者受力的矢量和为0。图6所示为构建的硅晶体60°滑移位错模型,模型中存在两个位错区域。两个位错区域呈中心对称,形成对称的位错偶极子。放大区域的原子为2个偶极子位错芯结构。

图6 硅晶体60°滑移位错模型
仿真模型大小为10nm×5nm×2.5nm,共包含24 644个原子。位错芯硅原子经过MS软件中CASTEP模块优化优化后得到新的原子位置,如图7所示。优化中的精度等级为Coarse等级,交换函数为广义梯度近似(GGA),选择默认选项PBE。60°滑移位错后,硅原子之间的Si-Si键长和位置都发生了一定变化。原子1与原子2之间的键长变为0.2716nm,原子2与原子3之间的键长变为0.2030nm,原子1与原子10之间的键长变为0.2008nm。硅晶体原有对称结构被打破,形成了新的结构。
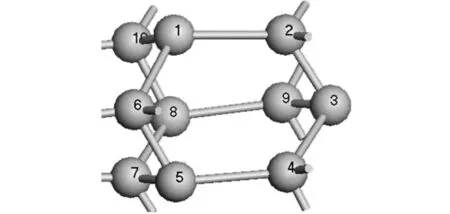
图7 位错芯硅原子位置
2.2 硅晶体螺旋位错模型
构建含有螺旋位错模型的方法,与构建硅晶体含有60°位错的方法相类似。在保持模型各个方向具有周期性边界条件的基础上,采用构建螺旋位错偶极子的方法构建硅晶体螺旋位错模型。具体方法是在模型中引入多个相同结构的螺旋位错芯,彼此间形成位错偶极子,保证元胞中的2个偶极子柏氏矢量方向相反,使得位错结构在整个模型的矢量和为0。
在理想的硅晶体模型中[10],以位错芯中心原子为原点,构建直角坐标系,取3个晶向为X、Y、Z方向。然后根据螺旋位错位移场方程[11]得到螺旋位错芯各个原子坐标。螺旋位移场方程为

式中,b为柏氏矢量;(xi,yi)为第i个原子的坐标;uz为第i个原子距离位错芯原子的距离。
3 螺旋位错模型仿真分析
3.1 螺旋位错芯的构造及模型的构建
根据螺旋位错位移场公式(式(1)),在理想硅晶体结构基础上构建螺旋场位错芯模型,如图8所示。
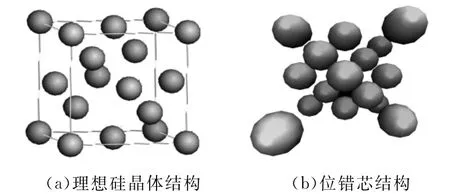
图8 硅晶体结构和螺旋位错芯结构
建立相应的仿真模型,在模型中构建螺旋位错芯结构,模型中共含有2个位错区域,2个区域对称形成偶极子。模型主体结构为理想单晶硅晶体结构。模型大小为10nm×10nm×10nm,分为牛顿层、恒温层和边界层,如图9所示。其中,牛顿层为工件和刀具作用区域。牛顿层原子在模拟过程中满足经典的牛顿运动定律。恒温层通过标定原子速度来控制原子动能大小,以调节整个系统的温度变化。边界层在模拟中不受外力作用,起到固定边界的作用。刀具为球形,由碳原子组成,结构为理想金刚石结构,在整个仿真过程中不考虑刀具作用,把刀具假定为刚体。

图9 仿真模型
整个系统总共含有62 258个原子,原子之间相互作用势采用Tersoff势能函数。刀具速度为20m/s,切削深度为1.0nm,切削总长度为6nm,时间步长为1fs(10-15s),恒温层调控温度范围为283~303K。
3.2 仿真结果分析
图10为仿真过程中刀具和工件相互作用图。当模拟进行至50ps时,磨粒还没接触工件,工件上的原子运动为简单的热运动。当模拟进行至100ps,这时磨粒开始切入工件,3个方向的切削力开始变化。图11所示为X、Y、Z三方向切削力变化曲线。当模拟进行至200ps时,磨粒已经完全进入工件,切削力变化较小,但由于切削长度较短,被去除的原子并未在刀具前堆积形成切屑。当模拟进行至400ps时,由于切削长度的逐渐增加,被去除的原子在刀具前方逐渐堆积形成切屑。
图12所示为加工过表面,可以清晰看到切削深度为1nm时,加工表面较为平整,螺旋位错结构并未对表面质量有较大的影响。加工表面处,原子出现回弹现象。切削过程中,工件原子晶阵在刀具的推挤作用下发生原子键断裂。随着刀具不断前移,处在刀具下方的原子在刀具挤压的作用下与已加工表层断裂的原子键结合,重构形成已加工表面变质层。处在刀具前方的原子在刀具的推挤作用下,脱离原有平衡位置,堆积在刀具前面形成切屑。

图10 含螺旋位错硅的磨削过程

图11 X、Y、Z三方向切削力变化曲线

图12 加工表面
在整个模拟过程中,螺旋位错结构对切削力变化影响较小。螺旋位错芯结构在刀具作用下并未发生结构上的变化。
4 结语
本文通过对位错晶格理论的研究,分析了理想硅晶体位错的形成过程。应用偶极子模型,提出含有60°滑移位错和含有螺旋位错的硅晶体模型的构建方法。采用此方法构建了含有螺旋位错的模型,通过对模型进行分子动力学仿真计算,研究了含有螺旋位错硅晶体纳米级磨削加工的机理。仿真结果显示,纳米级磨削中材料的去除主要来自于推挤作用,推挤作用使部分原子离开原有位置形成切屑和加工表面。加工后的表面会出现一定回弹现象,这种现象会影响加工表面的加工质量。
[1]Taylor G I.The Mechanism of Plastic Deformation of Crystals I-II[J].Proceedings of Royal Society A,1934,145:362-404.
[2]Peierls R E.The Size of a Dislocation[J].Proceedings of Physical Society,1940,52(1):34-37.
[3]Blumenau A T,Jones R,Frauenheim T,et al.Dislocations in Diamond:Dissociation into Partials and Their Glide Motion[J].Physical Review B,2003,68(1):014115.
[4]Tanata H,Shimada S,Higuchi M,et al.Mechanism of Cutting Edge Chipping and Its Suppression in Diamond Turning of Copper[J].Annals of the CIRP,2005,54(1):51-54.
[5]Komanduri R,Raff L M.A Review on the Molecular Dynamics Simulation of Machining at the Atomic Scale[J].Proceeding of the Institution of Mechanical Engineering,Part B:Journal of Engineering Manufacture,2001,215(12):1639-1672.
[6]Tanata H,Shimada S,Anthony L.Requirements for Ductile-mold Machining Based on Deformation Analysis of Mono-crystalline Silicon by Molecular Dynamic Simulation[J].Annals of the CIRP,2007,56(1):53-56.
[7]于思远,林滨,韩雪松,等.分子动力学仿真技术在超精密加工领域中的应用[J].中国机械工程,2002,13(1):22-25.Yu Siyuan,Lin Bin,Han Xuesong,et al.The Application of Molecular Dynamics Simulation to Ultraprecision Machining[J].China Mechanical Engineering,2002,13(1):22-25.
[8]张慧力.基于位错晶格理论的共价晶体中位错芯结构及Peierls势垒和Peierls应力研究[D].重庆:重庆大学,2010.
[9]杨立军,孟庆元,李根,等.Si晶体中60位错与空位缺陷相互作用的分子动力学研究[J].西安交通大学学报,2006,44(11):1352-1353.Yang Lijun,Meng Qingyuan,Li Gen,et al.Molecular Dynamics Simulation of Interaction between a 60 Dislocation and Vacancy Defects in Si Crystal[J].Journal of Xi’an Jiaotong University,2006,44(11):1352-1353.
[10]杨立军,孟庆元,李根,等.Si晶体中螺旋滑移特性的分子动力学研究[J].吉林大学学报(理学版),2007,45(2):260-261.Yang Lijun,Meng Qingyuan,Li Gen,et al.Molecular Dynamics Simulation of Screw Dislocation Motion Characteristic in Si Crystal[J].Journal of Jilin University(Science Edition),2007,45(2):260-261.
[11]Hirth J P,Lothe J.Theory of Dislocations[M].New York:Wiley,1982.

