基于神经网络的GPS高程拟合及其MATLAB实现
张占伟
(鞍山市辽地测绘技术有限公司)
1 引言
GPS 坐标是以地球质心为坐标原点的参心坐标,通过GPS测量获得的高程是以WGS-84椭球面为基准面的大地高。而在我国工程中采用的高程通常是以似大地水准面为基准面的正常高,大地高与正常高之差称为高程异常ζ。因此,在实际测量工作中大地高和正常高之间的转换成为工程技术人员所必须面临的一个难题。只要求出高程异常就可以方便的求得正常高。通常求取高程异常的方法是通过某种数学模型根据已知的GPS三维点位模拟求出未知点的高程异常。常见的数学模型有:曲线内插法、平面拟合法、多项式曲面拟合法、多面函数拟合法等等。由于数学模型具有一定的误差,对转换结果具有一定影响,因此相关人员提出了一种能有效有减少模型误差的影响的方法:神经网络法。由于神经网络方法比较繁杂,对于普通技术人员来说使用复杂。本文利用MATLAB提供的神经网络函数编程实现了GPS高程拟合,得出较好的效果。
2 MATLAB中的神经网络模型及函数
2.1 MATLAB中的神经网络算法模型
神经网络是以神经元为基本单位组成的具有非线性映射能力的网络,其实现是通过网络结构来实现,一般的网络结构如图1所示,从左到右分别是输入层,隐含层,输出层。

图1 BP神经网络原理图
2.2 GPS高程转换涉及的神经网络函数
在MATLAB中提供了大量的BP神经网络函数,其中GPS高程拟合涉及的主要函数如下:
(1)数据归一化函数与反归一化函数:premnmx、tramnmx和postmnmx,其目的是将输入分布在区间内,以便于网络的运行。
(2)BP神经网络创建函数:newff。本文涉及网络结构如下:net=newff(minmax(pn),,{'tansig','tansig','purelin'},'trainbr'),其中 minmax(pn 表示输入数据,表示网络为三层结构,其中输入层2个神经元,隐含层10个神经元,输出层 1 个神经元;每层对应的转换函数分别为'tansig','tansig','purelin',trainbr表示训练函数。
(3)BP神经网络初始函数init(net),用于对BP网络的初始化。
(4)BP神经网络训练函数train,用于对设定参数的网络进行训练。
(5)网络仿真函数 sim(net,pnewn),通过该函数可得GPS高程拟合结果。
3 基于神经网络的GPS高程拟合处理流程及其程序实现
3.1 基于神经网络的GPS高程拟合数据处理流程
(1)确定输入数据(GPS点平面坐标或大地坐标)和目标输出数据(正常高或高程异常),并对输入数据进行归一化处理。
(2)设计神经网络层数,并设定各层神经元个数。
(3)利用函数(newff或newfftd)创建神经网络。
(4)网络初始化与训练。
(5)通过sim函数以输入数据为依据进行网络仿真与复原。
(7)将待求点数据输入网络,并经反归一处理求出正常高或高程异常。
3.2 GPS高程拟合程序实现
依据上面所述GPS高程拟合数据处理流程,本文设计了一个3层神经网络,其输入层由2个神经元组成,输入元素为(x,y);隐含层由10个神经元组成,输出层由1个神经元组成;输出元素为高程异常ζ。部分程序代码如下:
学习部分:

3.3 GPS高程异常拟合程序运行结果
高程异常拟合精度及运行次数如图2所示,检核点的拟合残差结果如表1和图3所示。
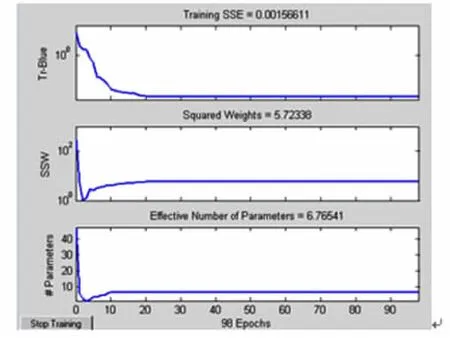
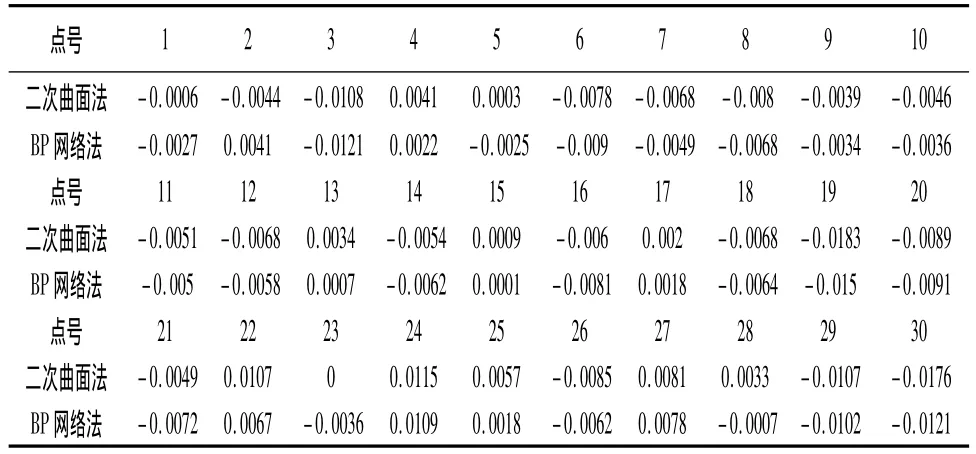
表1 GPS高程异常拟合残差
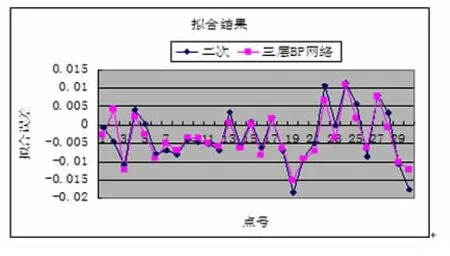
图3 GPS高程异常拟合结果
通过图2、表1和图3可以明显看出基于BP神经网络进行GPS高程转换的方法比二次曲面拟合法的效果要好很多,这与前面所述神经网络能有效避免数学模型带来的误差相符。BP神经网络和二次曲面拟合的误差在所有点上基本趋于一致。从统计的均方误差来看,神经网络方法比二次曲面拟合法更符合实际情况,拟合效果较好。
4 结论与展望
综上所述,BP神经网络在GPS高程转换方面具有一定的优越性,尽管其原理比二次曲面拟合法复杂;MATLAB为我们提供了BP神经网络网络工具箱及相关神经网络创建函数,为BP神经网络在高程转换中的应用提供了方便。
:
[1]黄声享,郭英起,易庆林.GPS在测量工程中的应用[M].北京.测绘出版社,2007.
[2]徐绍铨,张华海,杨志强等.GPS测量原理及应用[M].武汉:武汉测绘科技大学出版社,1998.
[3]鲁铁定,周世键,张立亭等.GPS高程转换的神经元网络方法分析[J].全球定位系统,2004(2):24-28.

