基于二次灰色马尔科夫预测的WSN状态判定算法*
林 蔚,李 波,韩丽红
(哈尔滨工程大学理学院,黑龙江 哈尔滨150001)
1 引言
在以监测为主要目的的无线传感网络应用环境中,监测的最终目标并不是要得到监测环境的全部实时数据,更主要的是要得到其异常数据,那么就不需要对全体监测数据进行传输。但是,数据何时出现异常是未知的,因此预测可以帮助提高监测效率,也即只需要传感器节点预测出下一个时间点数据的变异状态并将其发送到基站。本文提出一种无线传感器网络监测环境的状态预测思想:根据具体的监测环境和监测目的,制定不同的状态准则,以此预测下一个时刻的环境状态且用简单的符号或数字对状态做标识,将标识进行传输。
无线传感器网络节点采集数据的时间点和采集的数据具有离散的特性,且采集的数据仅与当时采样的监测环境有关系,即在某一时刻采集的数据仅依赖于现在而不依赖于过去,这一点正与马尔科夫模型的性质相同。马尔科夫预测[1~4]是基于马尔可夫链、根据事件的当前状况预测其将来时刻(或时期)变动状况的一种事件概率预测方法。它利用状态之间的转移概率矩阵预测事件发生的状态及其发展变化的趋势,因而比较适合长期的、随机波动性较大的预测问题[5]。由于无线传感器网络节点存储空间有限,不能存储大量的采样数据,直接将马尔科夫预测方法应用到无线传感器网络,会导致节点存储的堵塞。尽管灰色预测方法适用于时间短、数量少、波动不大的预测问题,但是灰色预测模型本身存在较大误差,得到的预测结果并不精确[6~9]。因此,针对无线传感器网络的特点,本文结合马尔科夫预测思想,对灰色预测模型进行改进,提出二次无偏灰色马尔科夫预测模型,解决网络状态预测问题,降低网络能量消耗,延长网络生命期。
2 二次无偏灰色预测模型
由于灰色预测模型本身存在较大的预测误差,不能得到较好的预测结果,如图1所示,直接将其应用到受多种因素影响的实时监测的无线传感器网络中,得到的预测数据精确度会很低,所以需要寻找一种能够弥补灰色预测本身所存在误差的方法,减弱其自身对数据预测的影响。为此,本节提出了二次无偏灰色预测方法,先对原始采样数据进行弱化处理,对处理后的数据采用二次拟合,之后建立二次无偏灰色预测模型。
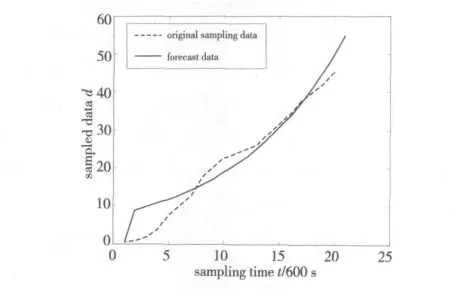
Figure 1 Gray measure schema图1 灰色预测示意图
首先将传感器节点采集的时间数据序列看作一个马尔科夫原始时间序列链,记为= ((t1,d1),(t2,d2),…,(tn,dn)),其中t是时间点,d 为t时刻的采样数据,n表示一个采样周期的时间点个数。
(1)采样原始数据序列,记为D(0)= (d(0)(1),d(0)(2),…,d(0)(n))。
(2)对原始数据弱化处理,得到弱化序列为:H(0)= (h(0)(1),h(0)(2),…,h(0)(n)),其中,h(0)(i)=(n)),i=1,2,…,n。
(3)对 H(0)一次累加,得到:D(1)= (d(1)(1),d(1)(2),…,d(1)(n)),其中k=1,2,…,n。
(4)一次模型记为d(1)(k+1)=λe-αk+γ,k=1,2,…,n,其中,λ=d(1)(1)-β/α,γ=β/α。
(5)根据灰色模型预测求得的α,对二阶拟合参数λ、γ进行估计:将一次模型写成矩阵形式,有D(1)=F(λ γ)Τ,其中:
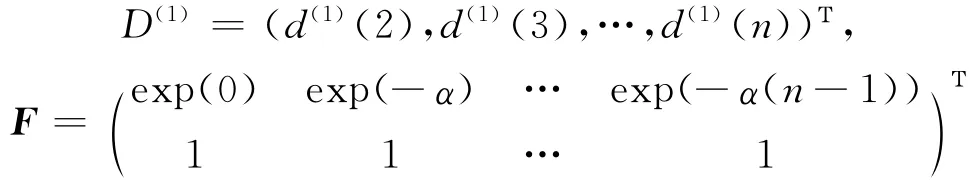
(6)采 用最 小 二乘 法 求 解:(λ γ)Τ=(FΤF)-1FΤD(1);
(7)计算无偏二次模型的参数:通过对模型分析知道,预测的数据 H∧(0)(k+1)与k有指数关系[10],则将具有指数趋势的预测数据记为:h∧(0)(k+1)=Αebk,生成一次累加序列:
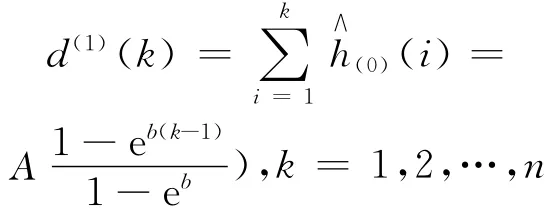
则有:
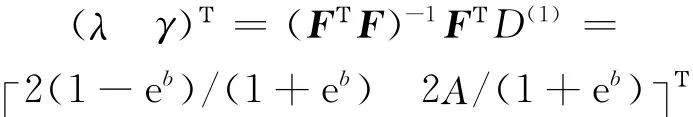
(10)根据弱化序列的预测值做强化运算,得到原始数据的预测值为:

二次无偏灰色预测模型首先对采样数据进行了弱化处理,减弱参加预测数据的波动性;之后进行二次灰色拟合,使得模型系数的预测更为准确;之后根据灰色预测模型预测数据的指数趋势,采用无偏方法,消除采用灰色预测产生的固有偏差,从两次运算的角度提高了模型预测的准确度,为状态预测的判定提供了准确的数据。到此,我们得到的是数据,但还没得到环境的状态,为此,还需要结合马尔科夫预测的思路进行状态判定。
3 马尔科夫状态预测
(11)根据二次无偏灰色模型求出原始数据序列的预测值d∧(0)(t)。
(14)根据检测的具体环境和用户的需求,在理想的状态下将数据进行划分。
无线传感器网络监测的环境是随机的某种未知状态,那么在对状态进行划分时要考虑环境因素,为了使算法更具一般性,下面根据一般状态马尔可夫链定义无线传感器网络中的状态。
3.1 定义
定义1 状态:指某一监测事件在某个时刻监测的某种结果。一般而言,根据所监测环境及其预测目标的不同,状态可以有多种划分方式。
定义2 状态转移过程:在监测事件的变化过程中,从一种状态转变为另一种状态,称为状态转移;监测事件的变化,随着时间所做的状态转移或者说状态转移与时间的关系,称为状态转移过程,简称过程。
3.2 状态判定准则
根据具体监测环境的目标不同,对于状态的划分也会不同,为了减少数据传输量,对于监测环境可能会出现的状态分别标识为⊗i,i=1,2,…,m,m≤n;同时规定,在进行数据传输时,仍需要根据实际需要来定义传输协议。下面给出适应于无线传感器网络的状态划分判定。
根据无线传感器网络的实际应用环境,将预测状态分为正常和异常两种状态,同时为了节省传输过程中能量的消耗,减少数据传输量,分别标识正常的状态为0,异常的状态为1;同时规定,正常状态时不发送任何数据,只传输预测到的异常状态(即标识状态为1时)的时刻点及异常数据。根据设定,误差相对值ε()k的取值为0或1。
3.2.1 初始化数据
初始化节点采样数据D(0)= (d1,d2,…,dn),其初始数据长度为n。
3.2.2 目标函数
以预测值与采样数据误差相对值ε()k的均值作为目标函数,使数据间的依存度最大,做出最优决策,记
3.2.3 判定准则
异常判定:对于下一个采样数据与预测值的误差的相对值,存在ε(k +1)>ω,则将其误差相对值状态记为1,说明检测结果是异常;
正常判定:对于下一个采样数据与预测值的误差的相对值,存在ε(k)≤ω,则将其误差相对值状态记为0,说明检测结果是正常。
(1)记判定状态空间为E = {0,1}。
(2)计算下一时刻数据点所处的状态:设状态空间 E = {0,1}的 转 移 概 率 矩 阵 为P =,其中0<λ,μ<1,且λ+μ≠1。(3)初始分布为π,有π0=πdi=()0=i=1,2,…,n。
(4)根据设定的状态划分得到初始分布,同时根据前面得到的k步转移概率为Pij()k=mij()k/Mi,式中mij()k为状态Ei经k步转移后到达状态Ej的次数,Mi为状态Ei出现的次数,由于数据序列的最后状态的转向不明确,故计算Mi时要去掉数据序列中最末的一个数据;当k=1时,即为一步转移概率Pij,其矩阵形式可记为
(5)由P(1)=P(0)P1,考察P(1)中的n个值,若Pkj=Pkl,则认为下一时刻系统最有可能由状态Ek转向状态El,即下一时刻最有可能处于状态El。
(6)由P(2)=P(1 )P1,…,P (n)=P(n-1)P1可知n时刻后系统最有可能所处的状态。
4 算法仿真与分析
由于在无线传感器网络进行监测的过程中,传感器节点会得到实时的监测数据,对于k步转移概率的应用起到的作用是大范围的预测,但不精确,为使无线传感器网络监测的预测更加准确,下述的仿真采用一步转移概率进行较为准确的预测。
4.1 仿真环境
本文实验在传感器节点作为数据提供方、传感器Sink节点作为接收方其处理能力一定的前提下,提供考虑预测的准确性问题。仿真工具为Matlab 7.0,采样间隔时间为600s。
4.2 仿真过程
(1)给出原始数据列d(0),如图2所示。
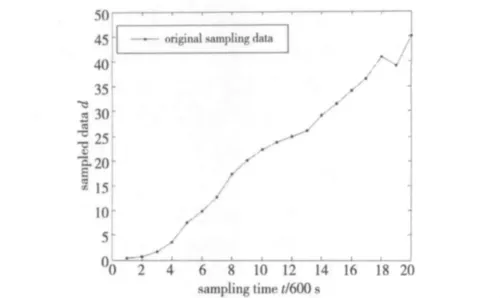
Figure 2 Monitorng data图2 监测数据
(2)经二次无偏灰色模型预测到预测值,如图3所示。

Figure 3 Raw data prediction图3 原始数据预测值
(3)求出预测值与采样数据的误差Δk,并计算误差的相对值ε()k,如图4所示。
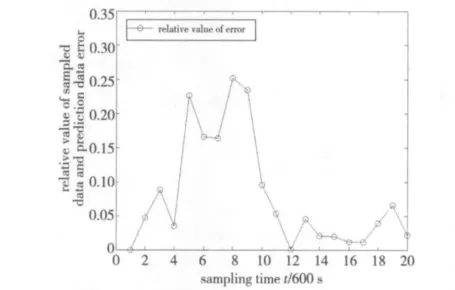
Figure 4 Original error relative value schematic diagram图4 误差相对值示意图
(4)状态划分:误差相对值ε()k均值,ω=8.02%;根据状态划分判定方法得到状态空间E={0,1},具体状态如图5所示。
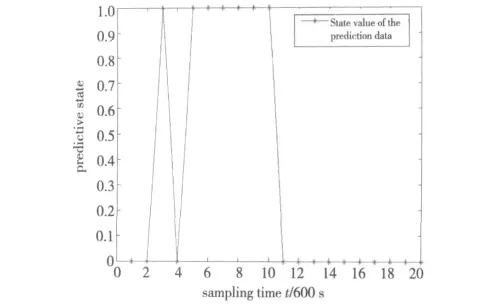
Figure 5 State schematic diagram图5 状态示意图
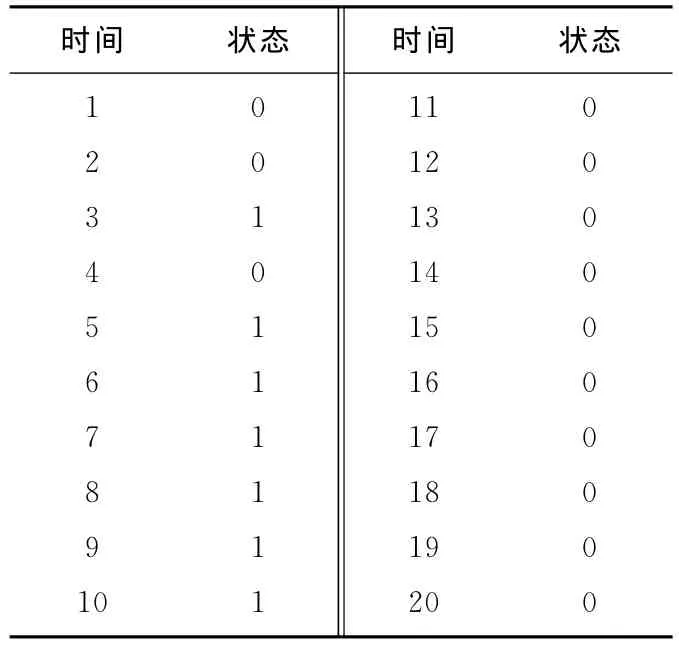
Table 1 State table表1 状态表
(6)初始分布π= (π0, π1)= (0.6316,0.3684)。
(7)P(1)=P(0)P1= πP1= (0.631 6,(8)maxPkj=Pk1=0.6316,所以下一个状
j态是0,误差相对值状态记为0,说明检测结果是在误差范围内,则不发送状态标识。
4.3 仿真结果分析
通过二次无偏灰色模型对数据进行预测的结果(如图3所示)可以看出,曲线拟合趋势与监测数据趋势大致相同,预测误差较小;经过仿真得到下一个时间点数据为=46.987 8,而实际的采样数据是d21=47.352 6,根据误差相对值的公式有误差相对值的平均值ω进行比较,有ε(21)<ω,所以灰色马尔科夫预测模型的验证结果同实际预测结果相同,预测也是较为准确的。仿真实验基本上涉及整个周期采样数据的各种数据,同时得到较大的压缩比,对于能量十分有限的传感器节点起到了节省能量的作用。但是,其中也有不足,从40 min到140min期间,由于数据波动大,使预测拟合偏离较大,可能是由于算法对原始数据弱化后减弱了波动趋势,导致拟合存在误差,还需要进一步讨论。综上所述,采用二次无偏灰色马尔科夫状态判定的方法既可以得到较好的数据预测,也可以对环境的状态进行准确的判定,还可以有效地减少整个网络的数据传输量。
5 结束语
根据无线传感器网络特点,本文在其监测环境中采取了状态判定,提出了二次无偏灰色马尔可夫预测模型。该模型与传统的数据压缩的本质有所不同,它将灰色模型和马尔可夫链模型的优点结合起来,并进行了改进,提高了预测精度。同时,根据监测的目的,只对判定的状态标识进行传输,不需要在汇聚节点或用户端对传输的数据进行解压缩,减少了能量消耗,对于延长整个网络的生命周期起着关键性的作用且计算过程不复杂,非常适用于能量有限的传感器节点。改进的模型给出了状态分类的判定方法,能够按概率特性对状态进行合理区别,提高状态预测的准确度,大幅度降低数据的传输量。
[1] Zimmermann M,Dostert K.Analysis and modeling of impulsive noise in broad-band line communications[J].IEEE Transactions on Electromagnetic Compatibility,2001,44(1):249-258.
[2] Ephraim Y,William J J.An EM algorithm for Markov modulated Markov processes[J].IEEE Transactions on Signal Processing,2009,57(2):463-470.
[3] Liao Rui-jin,Xiao Zhong-nan,Gong Jing,et al.Markov model for reliability assessment of power transformers[J].High Voltage Engineering,2010,36(2):322-328.(in Chinese)
[4] Wang Xian,Niu Dong-xiao.Forecasting on competition ability of electric power resource based on Markov chain[J].Modern Electric Power,2004,21(1):94-97.(in Chinese)
[5] Yi Hong.Methods to study of ship’s overall reliability universal model and ship reliability engineering[D].Shanghai:Shanghai Jiaotong University,2003.(in Chinese)
[6] Wang Li-xia,Xia Le-tian.The application in the prediction of stock market based on gray Markov chain model[EB/OL].[2009-08-05].http://www.paper.edu.cn.(in Chinese)
[7] Xue Xun-guo,Liu Bao-xin,Li Bai-chuan.The application in the prediction of road accidents based on gray Markov chain model[J].Chinese Journal of Ergonomics,2006,12(3):26-28.(in Chinese)
[8] Tang Na,Gui Yu-feng,Li Bao.Predict gas emiissing quantity of mining coal face wuth inproved Grey Markov model[C]∥The Fifth China Annual Conference on Uncertainty,2007:195-198.(in Chinese)
[9] Sun Xiang.Wireless sensor network data flow model on semi-Markow chain[M].Hebei:Hebei University of Engineering,2011.(in Chinese)
[10] Zhang Xin,Ren Yong-tai,Wang Fu-lin,et al.Prediction of annual precipitation based on improved Grey Markov Model[J].Mathematics in Practice and Theory,2011,41(11):51-57.(in Chinese)
附中文参考文献:
[3] 廖瑞金,肖中男,巩晶,等.应用马尔可夫链模型评估电力变压器可靠性[J].高电压技术,2010,36(2):322-328.
[4] 王贤,牛东晓.基于马尔可夫链的电力能源竞争力预测[J].现代电力,2004,21(1):94-97.
[5] 易宏.舰船总体可靠性通用模型及舰船可靠性工程的方法研究[D].上海:上海交通大学,2003.
[6] 王礼霞,夏乐天.灰色—马尔可夫链模型在股市预测中的应用[EB/OL].[2009-08-05].http://www.paper.edu.cn.
[7] 薛勋国,刘宝新,李百川.灰色马尔可夫链在道路交通事故预测中的应用[J].人类工效学,2006,12(3):26-28.
[8] 唐娜,桂预风,李宝.灰色马尔可夫模型应用于股指分析[C]∥第五届中国不确定系统年会,2007:195-198.
[9] 孙翔.基于半马尔可夫链的无线传感器网络能耗模型研究[M].河北:河北工程大学,2011.
[10] 张鑫,任永泰,王福林,等.基于改进灰色马尔科夫模型的年降水量预测[J].数学的实践与认识,2011,41(11):51-57.

