云计算环境下基于关联量的数据部署与任务调度＊

郭力争，赵曙光，姜长远

（1.东华大学信息学院，上海201620；2.河南城建学院计算机科学与工程系，河南 平顶山467036）

1 引言

研究人员依赖于一定的平台来执行科学工作流，解决数据密集型、计算复杂型等问题，如天文学、高能物理、地震监测［1］和生物信息学［2］，这样的科学工作流通常在本地集群和数据网格平台上执行［3］。云计算的出现为科研人员提供了执行科学工作流的又一个优秀平台［4］。在学术界，文献［5，6］探讨了在云计算平台上运行科学工作流的可行性，文献［7］总结了云计算平台运行科学工作流的优点。科学工作流的特点是要处理和传输的数据量通常巨大，达TB甚至PB级，另外科学工作流运行过程中也会产生大量的中间数据和一些最终的处理结果，因此，在利用云计算时遇到了一些新的挑战性问题，如数据部署和任务调度，主要表现为数据中心的不同集群处理能力不同，集群间网络性能有所不同，而且数据密集型应用所处理的数据量巨大，所以如何减少数据中心不同集群间的数据传输量、传输时间和数据传输次数就成为数据密集型应用的一个难题。一个科学工作流有一定数量的任务，每个任务要处理特定的文件，每个文件有不同的数据量和复杂性，并且这些文件间有一定的依赖关系，所以数据中心应合理分析这种关系，尽量减少流程执行过程中数据的移动和传输，提高数据中心的性能。

一些研究者在网格环境下致力于数据依赖性的研究，并应用到大规模科学工作流中。Filecules项目［8］基于数据的依赖对文件进行分组，结果显示了其分组策略在科学网格环境中对数据管理的有效性。BitDew［9］是一个基于桌面网格的分布式数据管理系统，不同于云计算中向用户提供服务，桌面网格的目的在于使用桌面计算机闲置的计算和存储资源。在BitDew中数据依赖被定义为数据的一个属性，该属性由用户预先定义。但是，在云计算环境下，所有的数据都存储在数据中心，供所有的用户使用，让用户预先定义数据的依赖关系是不切实际的。一些研究者研究了云计算环境下的数据部署和任务调度问题，Agarwal等人［10］考虑到在分布式环境下的数据部署问题，提出了一个自动的模式来处理存储限制和数据相互依赖问题。Cope等人［11］提出了启发式算法来获得对科学工作流存储超限的问题。Pandey等人［12］和 Ramakrishnan等人［13］讨论了数据敏感的科学工作流中的调度问题。但是，在这些研究中，文件在多个站点进行复制，这样会带来数据的传输问题。张春燕等人［14］提出了一种基于蚁群优化算法的云计算任务分配方法，该方法减少了处理请求任务的平均完成时间，提高了任务处理的效率；曾志等人［15］提出了海量数据集群环境计算的四叉树任务分配策略，该策略能有效地提高整体计算速度。但是，这些方法没有对数据关联进行分析，不能减少数据的传输。

针对上述问题，本文通过分析云计算环境下面向流程的数据密集型应用的特点，在全面考虑数据传输次数、数据传输量以及工作流执行性能的基础上，提出云计算环境下面向数据密集型应用的基于最大关联量的数据部署和任务调度策略。该策略一方面对数据集间数据依赖关系进行建模，并依此模型对数据进行聚类；然后通过K分割算法对聚类后的数据进行分割，数据中心的任务分配器根据分割结果进行部署和调度。

2 基本概念与问题描述

2.1 基本概念

定义2 数据集为工作流的任务需要处理的文件集：FS ＝ ｛f1，f2，…，fm｝。这些数据文件有的是输入数据，有的是输出数据。

定义3 T ＝ ｛t1，t2，t3，…｝表示科学工作流中任务的集合，ti＝ 〈runtime，fi〉，runtime表示每个任务运行的时间，fi表示i任务要处理的文件。

定义4 fi＝ 〈sizei，Ti，dci，linki〉表示科学工作流中编号为i的文件的数据集。其中，sizei表示文件的大小，Ti＝ ｛t1，t2，t3，…｝表示处理文件fi的任务的集合，dci表示文件被分配到的集群，linki＝｛in，out｝表示文件是输入还是输出。

定义5 trf为完成任务t所需要的文件集：trf＝ ｛f1，f2，…，fn｝。

定义6 tgf为执行任务t所产生的中间文件或输出文件集：tgf＝ ｛f1，f2，…，fn｝。

定义7 tim是执行任务i所需移动的文件集：

为了更好地分析资源部署和任务调度，首先对一些基本概念进行定义说明。

定义1 数据中心定义为一个集合C

2.2 问题分析与案例

科学工作流在云环境下运行的步骤如下：

步骤1 云计算服务商建立数据中心，用户可以按需申请使用。另一方面，数据中心也可以是科研院所建立的，免费供合作伙伴或个人使用。

步骤2 使用者运行科学工作流时，需要向云平台申请资源，并对云平台进行定制。比如申请使用的存储空间、计算能力、使用时间、使用方式等。

步骤3 在科学工作流运行之前，需要分析具体科学工作流的数据特点和任务特点，进行数据的逻辑部署。根据其结果，数据中心的任务分配器进行数据的部署和任务的调度。

步骤4 在科学工作流执行阶段，会产生中间数据，这些数据会被后续任务使用，把数据分配到最合适的集群，以减少数据的传输，提高性能。

下面以图1为例说明不同的数据部署和任务调度策略对数据移动次数和数据量的影响。

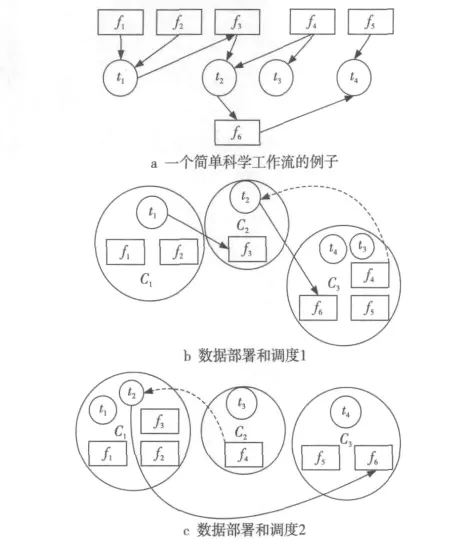
Figure 1 Instance of scientific workflows图1 科学工作流实例

图1 a是一个简单科学工作流的例子，其中四个输入文件f1、f2、f4、f5，两个输出文件f3、f6，四个任务t1，t2，t3，t4对应的数据集FS ＝ ｛f1，f2，f3，f4，f5，f6｝，任 务 集 T ＝ ｛t1，t2，t3，t4｝。具体数据内容为：f1＝ 〈200，t1〉，f2＝ 〈400，t1〉，f3＝〈100，｛t1，t2｝〉，f4＝ 〈500，｛t3，t2｝〉，f5＝ 〈300，｛t4｝〉，f6＝ 〈800，｛t4，t2｝〉。

科学工作流运行中数据集和任务之间并不是一对多或者多对一的关系，而是多对多的关系。从图1a中可以看出，f4同时被任务t2、t3使用，而任务t2同时使用f4、f3文件。由于在科学工作流中数据之间有相关性，所以将关系紧密的数据集尽量放置到同一个集群。在图1a中，如果把工作流分配到三个集群，按图1b中的数据部署和调度，由于t2∈C2需要使用f3，而f3∉C2，f3∈C1是t1产生的，即f3＝ ｛200，t1，C1，link ＝out｝，所以要把f3传输到C2。同样的原因，需要把f6传输到C3，f4传输到C2。因此，总共需要移动三次数据，移动的数据量为：100＋500＋800＝1400。如果按照图1c的部署，t1、t2要处理f1、f2、f3、f4，而 ｛t1，t2｝∈C1，｛f1，f2，f3｝∈C1，所以不需要移动数据，但是f4∈C2，而t2也要处理f4，所以应把f4传输到C1；同样，t4要处理f5、f6，而t4∈C3，f5∈C3，但f6∉C3，所以要把f6从C1传输到C3，t3要处理f4，但t3∈C2，f4∈C2，所以不需要移动数据，因此，只需移动两次数据，移动的数据量为：500＋800＝1300。

3 数据依赖性的定义与BEA算法

在科学工作流中有大量的数据，在本文中，不考虑数据的格式，把所有数据当作文件来处理。

3.1 数据关联性的定义

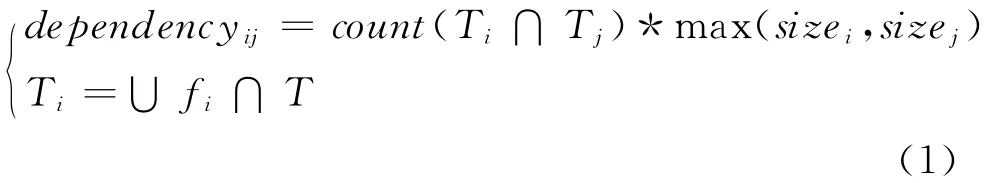
通过2.2节的分析，可以清晰地看到不同的部署方法、任务调度策略，对科学工作流产生的数据移动次数和移动量是不同的。执行每个任务，所需的数据必须位于同一个集群，否则就要把数据从其他的集群传输过来。如果一些数据集总是被相同的任务集使用，有理由相信，把这些数据集部署到同一个集群，再把相应的任务调度到此集群，会减少数据的移动量和移动次数，称这些数据集有依赖性。如果两个数据集同时被同一个任务使用，则说明这两个数据集有相关性；如果使用数据集的任务越多，数据越大，数据集间的关联性也越大。因此，我们定义最大关联量如下：该公式中各变量的含义见2.1节中的定义3和定义4。

3.2 基于BEA的聚类算法

键能算法 BEA（Bond Energy Algorithm）［16］被广泛应用于垂直分割分布式数据库系统中的大表。这是一个排列类型的算法，通过行和列的排列、分割，使矩阵中类似的元素放置在一起。BEA算法把关联矩阵AA（Affinity Matrix）作为输入，

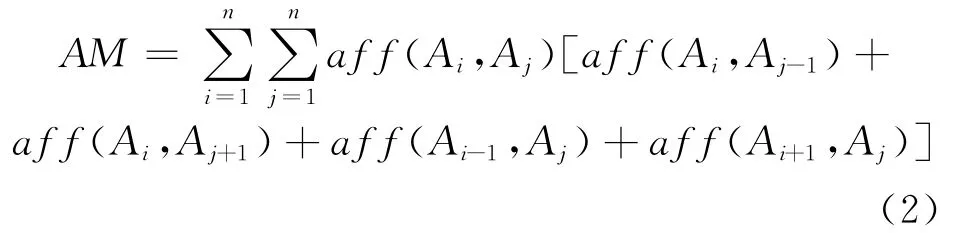
其中，n是矩阵的行或列数，aff（Ai，Aj）表示两列或两行相对于其他列或行的相近性。

约束条件为：

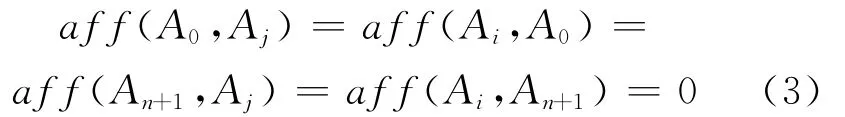
全局依赖量的约束条件说明，如果矩阵的一列元素被放置在CA最左列的左边或最右列的右边，则这两列的相近度量值为0，因为在这种情况下CA左边或右边没有邻居，它们在CA中还不存在。行处理同此。

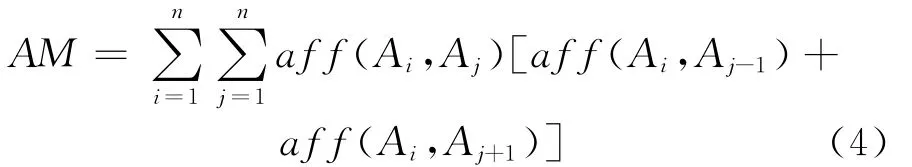
最大化的依赖量只考虑临近的邻居，因此导致了大的数据聚集在一起，小的数据聚集在一起。由于关联矩阵是对称的，因此，简化后的关联量定义如下：排列行和列形成一个聚类关联矩阵CA（Clustered Affinity Matrix）。行和列依据全局依赖量最大化进行。全局依赖量的定义如下：

BEA算法的基本思路如下：

初始化：任选一列

迭代

选择下一列并放置于矩阵中，使得全局的依赖量最大

重复

行的处理和列相同

由于输入的依赖矩阵是对称矩阵，所以列的顺序和行相同。

4 基于关联量聚类的数据部署与任务调度

基于关联量聚类的数据部署与任务调度分为以下几个步骤：原始数据的分析与关联矩阵的建立；BEA聚类、K分割的具体实现。

4.1 原始数据的分析与关联矩阵的建立

由于标准的科学工作流为XML文件格式，对原始数据的分析主要是分析XML文件包含多少个任务（tasknumber），每个任务的运行时间（runtime）是多少，每个任务需要处理的文件数（each＿task＿use＿file），文件名（filename）是什么，文件的大小（filesize），文件的输入输出（filelink），每个文件被多少个任务（each＿file＿used＿task）使用。

原始数据提取的大致过程如下所示：

filestr＝fileread（xmlfile）；／／读取XML文件

tasknumber＝get（filestr）；／／XML文件的任务数

for（each jobin filestr）

each＿job＿file＿number＝get（each＿job）；

runtime＝each＿job＿runtime；

filesize＝size；

filelink＝link；

filename＝file；

end

end

for（each file）

each＿file＿used＿task＝find（task use file）；

end

for（each task）

each＿task＿use＿file＝find（file in job）

end

下面详细说明关联矩阵的建立：关联矩阵是根据数据间的最大关联量建立的，最大关联量的定量计算通过公式（1）来进行。关联矩阵的建立过程如下所示：

1.for（each＿file）

2. file＿use＿task＝0；

3. for（each＿file＿use＿task）

4. if（other＿file＿use＿the＿task）

5. file＿use＿task＋1；

6. end

7. AA＝file＿use＿task；

8.end

9.for（each＿element in AA）

10. if（size（AAi）＞（size（AAi＋1））

11. AAi＝AAi＊size（AAi＋1）；

12. else

13. AAi＝AAi＊size（AAi）；

14. end

15.end

1～8行计算出每个文件被多少任务使用，即Ti∩Tj，9～15行计算出相互关联的两个文件中文件数据大的那个乘以关联的任务数并赋给关联矩阵对应的值。

4.2 BEA聚类与K分割的实现

BEA聚类算法首先通过聚类把关联矩阵转换为聚类矩阵，详细的算法实现在3.2节已阐述过。而云计算中的科学工作流通常有多个集群，聚集后就要考虑如何把这些关联数据分割成k个部分，部署到相应的集群。把这些关联数据部署到集群是个NP－hard问题，运用二元递归分割法来找到一个近似的最优解，K分割算法如下所示：

1.／／input：k，分割k个部分

2. CA：聚类矩阵

3. newlocInex：聚类分割后的列索引

4. filesize：每个文件的大小

5. filelink：每个文件的类型，in或out

6.／／output：partSet，k个分割部分

7.［p，CPt，CPb］＝partition＿algorithm（CA）；／／首先把CA分割为两个矩阵CMt，CMb，并求出分割点p

8.loop：CPt＝CAthe top part index／／分割的上部的列的索引

9.CPb＝CAthe downd part index／／分割的下部的列的索引

10.partSet（1）＝CPt；

11.partSet（2）＝CPb；

12.big＿index＝max（all has been partioned）／／最大部分的索引

13.［p，CMt，CMb］＝partition＿algorithm（partSet（big＿index））；对大的部分继续分割

14.go to loop

首先把聚类矩阵CA分割为两个部分，两个部分为 ｛f1，f2，…，fk｝和 ｛fk＋1，fk＋1，…，fn｝，分割成两个部分的标准是使如下的测量值最大化：

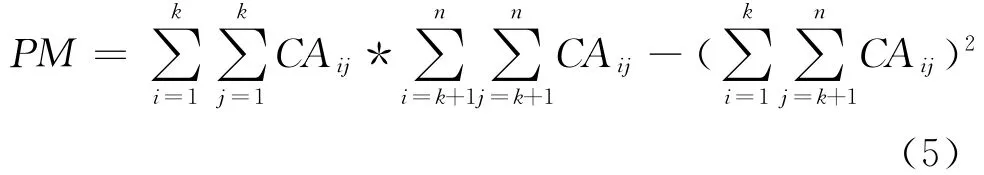
该测量值PM使得CA矩阵中关联性高的数据被分割到一起，关联性低的数据被分割到另一部分。基于此，分别计算k＝1，2，…，n－1，n，并选择使PM最大的k作为分割点把CA分割为两个部 分，分 别 为 CPt＝ ｛f1，f2，…，fk｝和 CPb＝｛fk＋1，fk＋2，…，fn｝。经过一次分割一个变为两部分，如果要把CA矩阵分割为k个部分，就要进行k－1次分割；进行k－1分割可以通过递归的方法完成，关键的问题是选择哪一部分进行继续分割。选择数据量最大的部分进行分割，这是为了云计算中数据传输和移动的方便而考虑的；反之，如果部分数据量巨大，传输和移动都比较耗时间，影响网络和数据中心的性能。K分割算法大致如下：第7行通过分割算法把聚类矩阵CA分割为CPt和CPb两个部分；第8行和第9行计算出AA经过BEA算法聚类为CA的矩阵的各个文件在CA中的索引；第10行和第11行分别把两个部分赋给part－Set；第12行计算已分割部分中数据量最大的下标；第13行继续分割直到分割为k个部分。

5 仿真环境的建立与仿真结果分析

5.1 仿真环境的建立

为了测试基于最大关联量的数据部署策略的效果，建立了以下仿真环境。测试硬件为：AMD Phenom® Ⅱ X4B95 3.0GHz，2GB RAM，Microsoft Windows XP environment。仿真结果是基于MATLAB R2009b实现的。为了更准确地测试算法的性能，运用标准CyberSahke科学工作流作为测试对象。这些工作流可以从Pegasus web page https：／／confluence.pegasus.isi.edu／display／pegasus／WorkflowGenerator下载。仿真结果基于关联量的策略简称KA，基于相关性的策略简称K，为了比较这两种数据部署策略，还使用了一种随机的数据部署策略Random。

Random部署：从XML文件提取出工作流的数据，通过BEA聚类算法形成聚类矩阵，再通过K分割算法分割为k个部分。

K部署：从XML文件提取出工作流的数据，基于相关性形成关联矩阵，把关联矩阵中的数据通过BEA聚类算法形成聚类矩阵，再通过K分割算法分割为k个部分。

KA部署：本项目提出的基于关联量的部署方法。

5.2 仿真结果及分析

运用以上的标准测试工作流，把四个测试工作流中的文件和任务分别部署和调度到3、6、9、12、15和18个集群，测试K、KA和Random策略的性能，其结果如图2所示。

图2给出的是当数据中心集群数量改变时文件移动量的变化趋势图。随着集群数量的增多，Random策略的文件移动量都在逐步上升；K策略在测试任务为30、50、100的情况下，文件首先会上升，当集群为12或15时达到稳定，当任务集为1 000时，文件的移动量会逐步上升；KA策略在测试任务为30、50、100时，文件会先上升，但是比K策略会早一点达到稳定；当任务集为1 000时K策略和KA策略文件移动的量都会逐步上升。可以明显看出，Random策略最差，KA策略比K策略性能优越。

原因分析：随着集群数量的增多，平均每个集群分得的数据集将减少，任务执行时调用其它集群数据集的可能性增加，导致数据传输量上升。但是，KA策略要优于K策略。

Figure 2 Amount of file movement with different clusters图2 集群数量对文件移动量的影响

图3 给出的是当集群数量改变时文件移动次数的变化趋势图：随着集群数量的增多，文件的移动次数也相应地增多，Random策略的文件移动次数几乎和集群数呈线性增长；K策略在测试任务为30、50、100的情况下，文件首先会上升，当数据中心为12或15时达到稳定，当任务集为1 000时，文件的移动量会逐步上升；KA策略在测试任务为30、50、100时，文件会先上升，但是比K策略会早一点达到稳定；当任务集为1 000时K策略和KA策略文件移动次数都会逐步上升，但KA策略要比K策略增长缓慢。

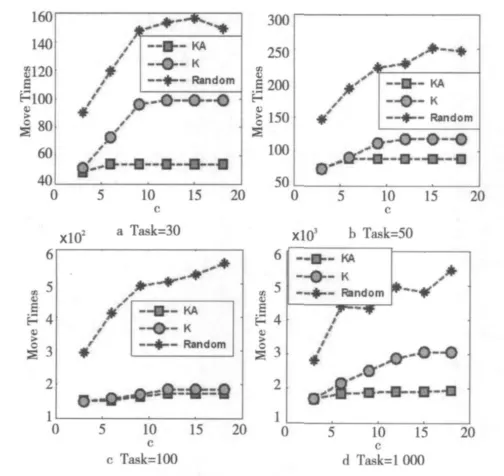
Figure 3 Times of file movement with different clusters图3 集群数量对文件移动次数的影响

图4 给出的是集群数量改变时任务性能的变化趋势图。设定集群为k时，集群的性能为1～k的一个随机数。由于集群数不同产生的集群的性能也不一样，所以在比较性能时从纵向比较，同一个任务同一个集群的三种不同的数据部署和调度策略进行比较。仿真结果表明：随着任务集的增加，任务的执行性能在不同的集群逐步上升，K策略和KA策略明显优于Random策略，KA策略稍微优于K策略。

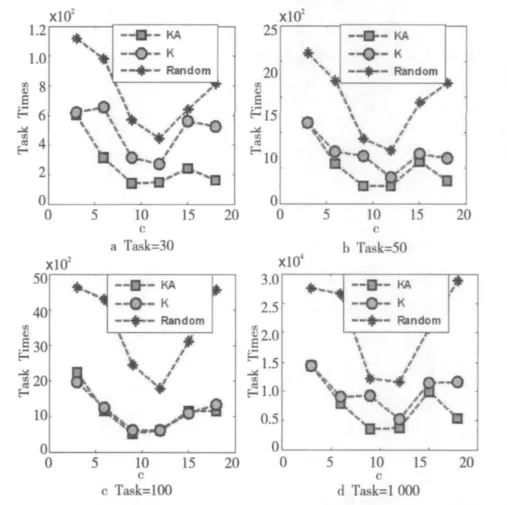
Figure 4 Task performances with different clusters图4 集群数量对任务执行性能的影响

6 结束语

本文对云计算环境下数据密集型应用科学工作流的基本概念进行了说明，对数据部署和任务调度进行了分析；通过以上分析提出了最大关联量的数学模型，基于最大关联量模型提取对科学工作流中的数据，形成关联矩阵；运用BEA算法对关联矩阵进行聚类形成聚类矩阵，然后通过K分割算法把聚类矩阵分割为k个部分；通过任务调度器把k个部分部署到相应的集群，任务调度到集群，完成任务的部署和调度。仿真结果表明，KA策略能有效地减少数据的移动次数和移动量，提高任务的性能，降低程序的复杂性。目前，本文策略没有考虑云计算的费用和能耗的优化问题。由于科学工作流中要处理的数据量非常大，云计算中根据传输数据的量来收取数据的传输费；科学工作流处理的任务复杂，在多个不同的集群对任务进行处理，造成能耗非常大，所以，下一步计划对云计算科学工作流中的费用、能耗问题进行研究。

［1］ Southern california earthquake center［EB／OL］.［2012－05－20］.http：／／www.scec.org.

［2］ Livny J，Teonadi H，Livny M，et al.High－throughput，kingdom－wide prediction and annotation of bac－terial non－coding rnas［J］.PLoS ONE，2008，3（9）：e3197.

［3］ Tera－Grid［EB／OL］.［2012－05－20］.http：／／www.teragrid.org／.

［4］ Weiss A.Computing in the clouds［J］.netWorker，2007，11（4）：16－20.

［5］ Deelman E，Singh G，Livny M，et al.The cost of doing science on the cloud：Themontage example［C］∥Proc of 2008 ACM／IEEE Conference on Supercomputing，2008：1－12.

［6］ Mehta G，Freeman T，Deelman E，et al.On the use of cloud computing for scientific workflows［C］.∥Proc of the 4th IEEE International Conference on e－Science，2008：640－645.

［7］ Juve G，Deelman E，Vahi K，et al.Scientific workflow applications on amazon ec2［C］∥Proc of Workshop on Cloudbased Services and Applications in Conjunction with the 5th IEEE e－Science，2010：59－66.

［8］ Doraimani S，Iamnitch A.File grouping for scientific data manag－ement：Lessons from experimenting with real traces［C］∥Proc of the 17th International Symposium on High Performance Distributed Computing，2008：153－164.

［9］ Fedak G，He H，Cappello F.BitDew：A programmable environment for large－scale data management and distribution［C］∥Proc of 2008ACM／IEEE Conference on Supercomputing，2008：1－12.

［10］ Agarwal S，Dunagan J，Jain N，et al.Volley：Automated data placement for geo－distributed cloud services［C］∥Proc of the 7th USENIX Conference on Networked Systems Design and Implementation，2010：2.

［11］ Cope J M，Trebon N，Tufo H M，et al.Robust data placement in urgent computing environments［C］∥Proc of the 2009IEEE International Symposium on Parallel ＆ Distributed Processing，2009：1－13.

［12］ Pandey S，Buyya R.Scheduling data intensive workflow applications based on multi－source parallel data retrieval in distributed computing networks［EB／OL］.［2012－05－15］.http：／／www.cloudbus.org／reports／MultiDataSourceWorkflowCloud2010.pdf.last.

［13］ Ramakrishnan A，Singh G，Zhao H，et al.Scheduling dataintensive workflows onto storage－constrained distributed resources［C］∥Proc of the 7th IEEE International Symposium on Cluster Computing and the Grid，2007：401－409.

［14］ Zhang Chun－yan，Liu Qing－lin，Meng Ke.Task allocation based on ant colony optimization in cloud computing［J］.Journal of Computer Applications，2012，32（5）：1418－1420.（in Chinese）

［15］ Zeng Zhi，Liu Ren－yi，Zhang Feng，et al.A policy of task allocation base on distributed cluster computing towards cloud［J］.Telecommunications Science，2010（10）：30－34.（in Chinese）

［16］ McCormick W T，Sehweitzer P J，White T W.Problem decomposition and data reorganization by a clustering technique［J］.Operations Research，1972，20（5）：993－1009.

附中文参考文献：

［14］ 张春艳，刘清林，孟珂.基于蚁群优化算法的云计算任务分配［J］.计算机应用，2012，32（5）：1418－1420.

［15］ 曾志，刘仁义，张丰，等.面向云的分布式集群四叉树任务分配策略［J］.电信科学，2010（10）：30－34.