分布式OD运载网络中物流绿色轨迹监测系统的布局优化＊

李淑琴，杨 斌，胡志华，2

（1.上海海事大学物流研究中心，上海201306；2.同济大学经济与管理学院，上海200092）

1 引言

物流的环境效益和社会责任备受关注，绿色物流的研究对于经济、社会以及环境之间的协调发展具有重要的理论意义和实践意义。Murpy等人［1］对绿色物流的重要性、发展水平、动机和障碍等问题展开研究。单丽辉［1］提出基于物流网络的物流资源整合模式。肖丁丁和张文峰［2］运用图论与矩阵工具从企业、政府和环境层面进行系统分析。Ubeda等人［3］考虑业务盈利能力对环境的影响，在案例研究中将最大限度减少CO2排放作为评价标准。Caniato等人［4］以服装业为例来研究供应链的环境可持续发展问题。Harris等人［5］在选址模型中考虑提高车辆利用率减少物流成本与能耗。朱庆华和窦一杰［6］提出绿色供应链管理战略中生产商间的三阶段博弈模型。

物流绿色轨迹监测系统通过在相应道路上设置监测器，构造监测网络识别和记录物流网络中物流车辆和路段运输量，从而获得物流网络中的“绿色轨迹”信息，实现对区域“绿色度”的评价。OD（Origin Destination）流是交通研究的基本工具，在物流背景下拓展为具有起止位置的运输需求。Guo和Huang［7］在研究如何监测和评估网络中交通流量时，建立01整数规划模型，研究OD流路径选择的随机性。Nie和Zhang［8］研究基于柱生成算法的动态OD流需求估算问题。国内外很多学者将混合整数规划、多目标规划和启发式算法等运用到物流网络布局优化的研究中。Thanh等人［9］建立混合整数规划模型优化物流网络；Pishvaee等人［10］建立物流网络规划的确定性混合整数规划模型和随机规划模型。Harris等人［5］通过建立多目标优化模型，评价CO2排放对基础设施成本的影响。马祖军和代颖［11］建立逆向物流网络优化的混合整数规划模型。狄卫民［12］为回收物流网络建立随机规划模型。本文主要通过建立一个多目标混合整数规划模型来研究物流绿色轨迹监测系统的布局优化问题。

2 问题定义与分析

物流绿色轨迹监测系统的目的是对物流网络中通过的物流车辆进行识别和监控，实现对道路交通流量、能耗水平和污染程度等指标的监测。为达到这个目的，需要回答以下问题：如何在已知节点、道路以及OD流分布状况的运载网络中建立物流绿色轨迹监测系统？即在监测器数量和能力有限的情况下，如何合理部署监测系统的位置；监测器的数量为多少时监测系统的能力最优？如图1所示，在具有10个节点的物流网络中，部署由6个监测器构成的绿色轨迹监测网络，对通过16个路段的车辆进行监测。

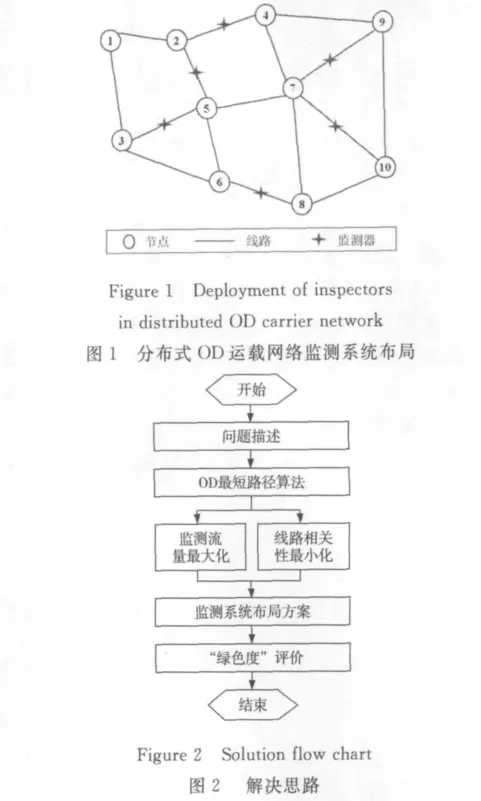
采用图2所示的步骤进行研究。首先，对已知的分布式OD运载网络，考虑到节点间的线路分布，计算出任意两节点的最短距离。对OD运载网络中的线路以最短路径进行估计：根据最短距离计算过程，得出每条OD流所经过的最短距离，以及每条OD流经过的路径。然后，考虑监测器的数量与总成本，根据流量大小和相关性来确定安装监测器的位置集合。

3 模型

下面对问题进行进一步界定：（1）分布式OD运载网络是一个图（Graph），包括物流网络的所有节点及节点之间的路线；（2）运载需求由每条OD流的起始点及其流量确定；（3）由O和D确定的路径在最短路径基础上具有一定随机性，即该需求途经的道路可能并不完全确定；（4）运输本身的外包情况并不熟悉，管理机构只能通过采样的方式获得“绿色”评价数据；（5）物流绿色轨迹监测系统中监测器选择安装在线路上，避免不同线路的起始点有交集，并且对每条线路不考虑流量限制。

3.1 参数和决策变量

根据以上研究问题的说明和假设条件，相关的模型参数说明如下。

（1）集合

①N＝ ｛1，2，…，NN ｝ ：物流网络中所有节点的集合；

②E＝ ｛1，2，…，NE ｝ ：物流网络中所有线路的集合；

③OD ＝ ｛1，2，…，NOD ｝ ：物流网络中所有OD流的集合。

（2）参数

①Da：OD流a∈OD上起始点间的流量；

②Pa，r∈ ｛0，1｝：Pa，r＝1表示OD流a∈OD经过线路r∈E；

③S：表示监测系统中安置的监测器数量；

④Vr：表示经过线路r∈E的OD流的总数量；

⑤RELi，j：表示线路i∈E和线路j∈E的相关性，即同时经过线路i∈E和线路j∈E的所有OD流的流量之和。

（3）决策变量

①xr∈ ｛0，1｝：xr＝1表示选择在线路r∈E上安装监测器，否则xr＝0；

②yi，j∈ ｛0，1｝：yi，j＝1表示同时在线路i∈E和线路j∈E上安装监测器，否则yi，j＝0。

3.2 目标函数

为了达到监测系统的效用与合理性，并兼顾经济效益，目标函数式（1）最小化分布式运载网络中任意两条线路之间的相关性。

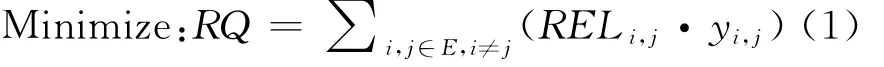
其中，RELi，j表示第i条线路和第j条线路之间的相关性，即同时经过这两条线路的OD流的流量之和，通过式（2）计算。

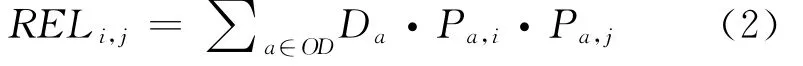
RQ越小，表示监测系统中部署的监测器所监测到的重复的OD流流量越少，从而监测系统的监测能力也就越强，所获得的样本数据越全面。目标函数式（3）最大化所有安装监测器的线路所能监测到的OD流的总数量。

其中，Vr＝ ∑aPa，r，表示在既定的运载网络中，当假定OD流都能以最短路径运行时，第r条线路上经过的所有的OD流的条数，即第r条线路所能监测到的OD流条数。VQ越大，表明监测系统所覆盖的监测范围越大。目标式（1）和式（3）之间相互影响，综合考虑这两个目标函数，可以对绿色轨迹进行全面评价，得到合理的监测网络部署方案。

3.3 约束条件

约束函数式（4）通过x定义y，当xi和xj同时为1时yi，j＝1，否则为yi，j＝0。约束函数式（5）对监测器数量进行约束。

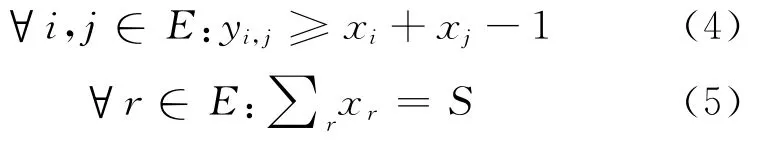
综合以上关于决策变量、目标函数和约束函数的定义，得到多目标01整数规划模型（P1）。

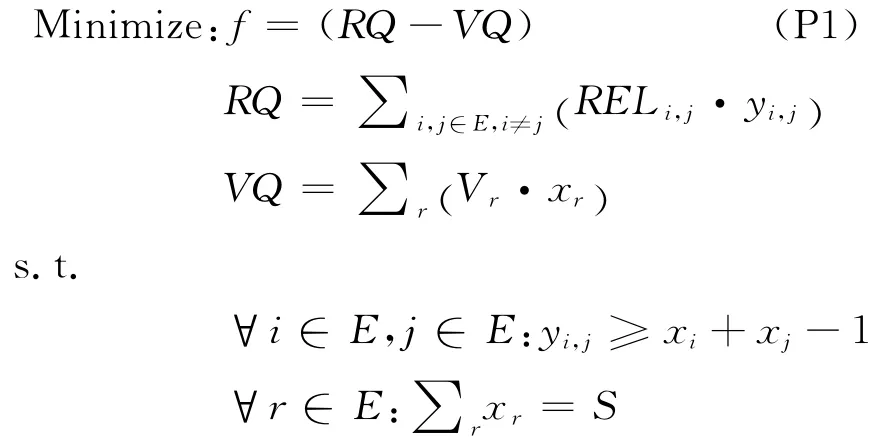
3.4 OD流网络的最短路径算法

从模型（P1）可知，OD流网络中的最短路径问题是一个基本问题。算法1在Dijkstra算法的基础上提出了分布式OD运载网络中求OD流最短路径的算法。

算法1 生成OD流的最短路径算法

输入：

N：节点的集合；

Xn：节点n∈N的横坐标；

Yn：节点n∈N的纵坐标；

E：线路的集合；

Sr∈E：线路r∈E的起点；

Tr∈E：线路r∈E的终点；

OD：OD流的集合。

输出：

W：Graph中任意节点之间的距离矩阵；

L：从始点O到终点D的最短距离；

Z：从OD流的始点O到终点D的最短路径；

Pa，r：任意一条OD流a是否经过线路r。

步骤：

Step 1 准备W ：将矩阵元素的默认值设置为无穷大，对角线元素设置为0：

∀i，j∈N：W（i，j）＝INF ；

∀i∈N：W（i，i）＝0。

Step 2 初始化W（i，j）：根据E 集合设置由线路直接连接的边：

∀r∈E：W（Sr，Tr）＝W（Er，Tr）＝

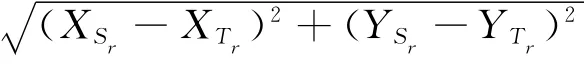
Step 3 根据Dijkstra算法求解任意节点间的最短距离：

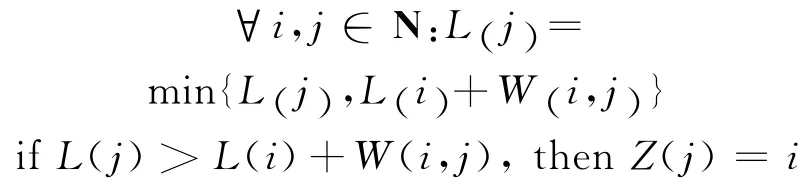
其中，（）L i表示从始点Oa到节点i的最短距离；Z（）j表示从OD流的始点Oa到节点j的最短路径上j点的前一个点，且Z（Oa）＝0；

／／L＝min｛L（Da），L（k）＋W（k，Da）｝，∀k∈N

if L（Da）＞L（k）＋W（k，Da），then Z（Da）＝k，L即为OD流从始点Oa到终点Da的最短距离。

Step 6 根据Step 5生成的OD流的最短路径Z，寻找其经过的线路：

∀a∈OD：将Z中所经过的点两两依次组成线路Ei，j；在集合E中找到这些线路Ei，j所对应的线路标号r，令Pa，r＝1。

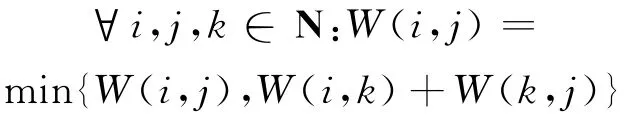
Step 4 准备矩阵P，即将矩阵元素的默认值设置为0：

Step 5 根据Dijkstra算法求解OD流的最短路径：

4 仿真

下面通过仿真实验验证模型（P1）和算法1的有效性，并对模型结果进行分析。分布式OD运载网络及其线路和节点网络如图3所示。

4.1 基本参数设置

如图3所示，区域中共有10个路口节点和16条直接相连的线路，且在整个运载网络中存在分布式OD流运载任务，直接连接的线路长度如图中路段上的数值表示。在下面的实验中，随机生成90个OD流构成集合OD，每个OD流的起点和终点在1～10中随机选择，而OD流的流量则通过均匀分布DEM ～U （10，50）随机生成。90条OD流及其运载量的具体分布见图4，可以发现该运载网络中OD流的运载量大致在30集卡单元上下波动。

4.2 仿真结果与分析

用Matlab.R 2011a编写了算法1的程序，模型采用Lingo 9.0进行求解，运行环境均为：Intel（R）Core（TM）i3－2310MCPU ＠2.10GHz，内存2GB。

根据算法1采用Matlab求出图3所示运载网络中生成的所有OD流的最短路径，以及Pa，r分布矩阵，即第a条OD流是否经过第r条线路的分布矩阵；在此基础上，对模型进行仿真。

模型（P1）是一个双目标模型，两个目标相互影响。利用帕累托最优准则权衡两个目标函数对于整个监测系统布局的影响。通过不同的权重分配，来获得不同的配置方案。首先，分别给两个目标函数设权重，其中目标RQ的权重为W1，目标VQ的权重为W2，且有W1＋W2＝1，W1≥0，W2≥0。通过式（6）聚合转化为单目标，通过调整W1和W2寻找Pareto解。

min f＝RQ·W1－VQ·W2（6）

设定W1从1～0以0.01的幅度递减；在不同的监测水平下，即在监测器数量分别为S＝4、S＝5和S＝6的情况下，分别运行100次得到的结果如表1所示。由表1可见，随着监测器数量的增加，帕累托不可公度解的数量也在增加。

在图5中，以目标函数RQ为横坐标，目标函数VQ为纵坐标，结合表1的结果可以得到：在不同的监测水平下，随着监测器数量的增加，监测系统所能覆盖的范围增大；而在同一监测水平下，随着线路之间的相关性水平的增高，监测系统所覆盖的OD流条数也逐渐增加，并渐趋于平稳。通过对比分析，相关性水平RQ的值在1 000～2 500比较合理，此时所得到的解具有比较好的收敛性。

Table 1 Pareto results of the monitoring system layout under different monitoring levels表1 不同监测水平下的监测系统布局的Pareto结果

5 结束语

在OD运载网络布局优化的基础上，建立“绿色轨迹监测系统”布局的多目标整数规划模型，目的是为监测设备有限的监测网络提供兼具经济效益和环境效益的配置方案，为此设计分布式OD运载网络中计算OD流最短路径的算法。采用渐变加权将多目标化为一系列单目标问题求解Pareto最优解集，并提出绿色轨迹监测的线路相关性衡量方法，对物流背景下一般监控网络布局与优化问题的解决具有参考价值。进一步的研究将突破网络规模限制，采用启发式算法来解决大规模的监测系统布局问题；考虑OD流路径选择时最短路径本身的随机性，同时考虑线路交通流量等限制因素，OD流路径应当存在k－最短路的选择；另外，通过融入客户绿色偏好和污染量分析等因素进一步拓展模型与算法的研究。

［1］ Murphy P R，Poist R F，Braunschweig C D.Role and relevance of logistics to corporate environmentalism：An empirical assessment［J］.International Journal of Physical Distribution and Logistics Management，1995，25（2）：5－19.

［2］ Xiao Ding－ding，Zhang Wen－feng.Key element analysis for green logistics development by using decision making trial and evaluation laboratory method［J］.Industrial Engineering Journal，2010，13（1）：52－57.（in Chinese）

［3］ Ubeda S，Arcelus F J，Faulin J.Green logistics at Eroski：A case study［J］.International Journal of Production Economics，2011，131（1）：44－51.

［4］ Garcia F A，Marchetta M G，Camargo M，et al.A framework for measuring logistics performance in the wine industry［J］.International Journal of Production Economics，2012，135（1）：284－298.

［5］ Harris I，Naim M，Palmer A，et al.Assessing the impact of cost optimization based on infrastructure modeling on CO2emissions［J］.International Journal of Production Economics，2011，131（1）：313－321.

［6］ Zhu Qing－hua，Dou Yi－jie.A game model for green supply chain management based on government subsidies［J］.Journal of Management Sciences in China，2011，14（6）：86－95.（in Chinese）

［7］ Guo R－Y，Huang H－J.Network traffic flow evolution model considering OD demand mutation［J］.Systems Engineering－Theory ＆Practice，2009，29（1）：118－123.

［8］ Nie Y，Zhang H M.A variational inequality formulation for inferring dynamic origin－destination travel demands［J］.Transportation Research Part B：Methodological，2008，42（7－8）：635－662.

［9］ Thanh P N，Bostel N，Péton O.A DC programming heuristic applied to the logistics network design problem［J］.International Journal of Production Economics，2012，135（1）：94－105.

［10］ Pishvaee S，Jolai F，Razmi J.A stochastic optimization model for integrated forward／reverse logistics network design［J］.Journal of Manufacturing Systems，2009，28（4）：107－114.

［11］ Ma Zu－jun，Dai Ying.Optimization model for reverse logistics network design for product recovery［J］.Journal of Industrial Engineering／Engineering Management，2005，19（4）：114－117.（in Chinese）

［12］ Di Wei－min，Hu Pei.Optimal design of returned logistics network with stochastic parameters of continuous distribution［J］.Chinese Journal of Management Science，2007，15（3）：40－46.（in Chinese）

附中文参考文献：

［2］ 肖丁丁，张文峰.基于DEMATEL方法的绿色物流发展关键因素分析［J］.工业工程，2010，13（1）：52－57.

［6］ 朱庆华，窦一杰.基于政府补贴分析的绿色供应链管理博弈模型［J］.管科科学学报，2011，14（6）：86－95.

［11］ 马祖军，代颖.产品回收逆向物流网络优化设计模型［J］.管理工程学报，2005，19（4）：114－117.

［12］ 狄卫民，胡培.含有连续型随机参数的回收物流网络优化设计［J］.中国管理科学，2007，15（3）：40－46.