多目标模拟退火算法及其应用研究进展＊

李金忠，夏洁武，曾小荟，曾劲涛，刘新明，冷 明，孙凌宇

（井冈山大学电子与信息工程学院，江西 吉安343009）

1 引言

模拟退火SA（Simulated Annealing）算法［1］是由Kirkpatrick等于1983年首次提出的一种求解大规模组合优化问题的有效算法，该算法是基于Monte Carlo迭代求解策略的随机寻优算法，源于热力学中固体物质的退火过程与一般组合优化问题之间的相似性，在一给定初温下，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解。因SA独特的优化机制及其对问题信息依赖较少，通用性、灵活性较强而在优化领域得到了广泛的应用，其在多目标优化领域的研究近年来也得到了一定的发展。传统的SA算法只针对单个优化目标进行求解，解的优劣很容易比较，而在多目标问题中，各个目标可能是相互冲突的或者相互独立的，无法像单目标问题的解那样直接进行优劣比较。近若干年来也有一些研究成果结合多目标优化问题的特性，根据SA的思想，设计多目标模拟退火算法，用来解决多目标优化问题。多目标模拟退火MOSA（Multi－Objective Simulated Annealing）算法的研究始于1985年，早期的工作还包括Ulungu等和Serafini等［2］设计的一个完整的MOSA，并将其应用于多目标组合优化问题。由于物体退火与多目标优化问题之间的本质联系，SA适合扩展并应用于多目标优化问题的求解。MOSA的出现为多目标优化问题的求解开辟了一条新的途径，在多目标优化算法中也已表现出良好的性能和前景。

2 MOSA算法基本框架

当前，已有多种MOSA算法被提出，根据近二十年来不同研究者所设计的 MOSA算法［2～23］，本文对MOSA算法进行了归纳，统一于基本框架内。基本MOSA算法描述如下：

步骤1 对算法的相关参数进行初始化，如初始温度、迭代次数等。

步骤2 随机产生初始解X，计算其所有目标函数值并将其加入到Pareto解集中。

步骤3 给定一种随机扰动，产生X的邻域解Y，计算其所有目标函数值。

步骤4 比较新产生的邻域解Y与Pareto解集中的每个解并更新Pareto解集。

步骤5 如果新邻域解Y进入Pareto解集，则用Y替代X，并转到步骤8。

步骤6 按某种方法计算接受概率。

步骤7 如果Y未进入Pareto解集，则根据接受概率决定是否接受新解，如果新解被接受，则令其为新的当前解X，如果新解未被接受，则保留当前解。

步骤8 每隔一定迭代次数，从Pareto解集中随机选择一个解，作为初始解，重新搜索。

步骤9 采取某种降温策略，执行一次降温。

步骤10 重复步骤3～步骤9，直到达到最低温度，输出结果，算法结束。

3 典型MOSA算法分析

在20世纪90年代，国际上关于MOSA算法的文献较多，虽然最近几年也发展了一些MOSA算法，但目前主要是应用MOSA算法解决具体问题。本文将阐述几种典型的MOSA算法。由于SA算法设计的关键是接受准则和冷却进度表［2，3］，因此，本文将重点讨论多目标条件下如何设计接受准则和冷却进度表，并对各种方法进行分析。

3.1 UMOSA

UMOSA［4，5］算法使用加权聚合法将多维标准空间映射到一维标准空间，它构建了一个潜在有效解列表，这些解不被任何其他产生的解所支配。根据决策者的选择，UMOSA算法适应于通过交互方式产生满意的结果给决策者。对单目标优化问题，坏解的接受概率是唯一和无二义性的，而对于多目标优化问题，从当前位置移动到新位置存在三种可能：（1）新解的所有目标都得到了改进，即新解支配当前解，以概率1接受；（2）新解的某些目标函数得到了改进，而另一些目标函数变差了，即新解和当前解彼此不受支配，此时所提出的策略必须能区分这些彼此不受支配的解；（3）新解的所有目标函数都变差了，即当前解支配新解，此时，接受概率必须考虑当前解和新解之间的距离。Ulungu等使用加权聚合法综合考虑了以上三种情况，提出了一种新的接受准则：

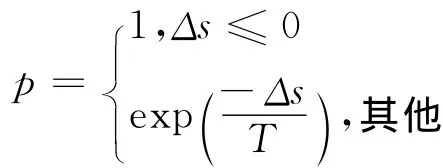
其 中，Δs ＝s（f（y），λ）－s（f（x），λ），s（F，λ）＝为权重向量。

UMOSA算法在计算接受概率时仅仅考虑新解与当前解之间的直接比较，导致一些良好的新解在搜索过程中可能被拒绝，于是 Haidine等［6］在UMOSA算法的基础上，提出了一种多情形的多目标模拟退火算法MC－MOSA。该算法改变了原算法的接受准则，分多种情形计算接受概率（其计算方法详见文献［6］），从而改善了UMOSA算法，获得了更好的性能，可产生更多能到达Pareto前沿的解。同时，作者也提出了MC－MOSA算法的三种变体：重复退火 MC－MOSA、快速退火 MCMOSA、两阶段退火MC－MOSA。

3.2 PSA

Czyzak等［7］对UMOSA算法进行修改，提出了Pareto模拟退火算法PSA。为了改变目标函数的接受概率，该算法在每一次迭代中，用一系列称为产生样本的解来控制目标函数权重的大小。如果没有一个最靠近样本x的非劣解x′或者对x进行第一次迭代，则设置随机权值∀λi≥0，∑λi＝1；否则，对每个目标函数fi，设置其权值为：

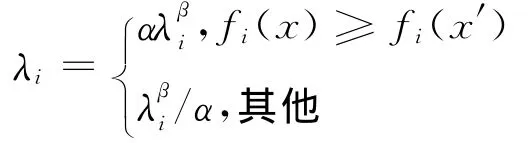
其中，α＞1。

通过对权重大小的控制，可以增加或降低某个特定目标的接受概率，从而保证所产生的解具有良好的多样性。PSA算法是以概率p ＝ min（1，接受新解。

上述MOSA算法是先按照加权聚合法对多个要优化的目标进行聚合，然后依据单目标SA算法进行求解。所谓加权聚合法是对要优化的每个目标，依据不同目标的重要性分别赋予一个权重，通过对所有目标加权聚合到一个目标函数中，将多目标优化问题转换成单目标优化问题。这是一种先决策后搜索的寻优模式，本质上仍然属于单目标优化。这种方法的优点是实现简单、易于使用，计算效率比较高，同时可以得到一个很好的优化解；缺点是带有一定的主观性，不符合多目标优化问题自身的特点。

它们在求解多目标优化问题时存在的缺陷主要体现在：

（1）采用这些算法求解通常每次优化只能得到一个最优解，且该解的获得与转换过程中目标参数权重的设定有很大关系。若要获取更多的最优解，需通过多次调整参数权重、多次运行该算法来进行寻优，由于各次优化过程相互独立，导致得到的解往往不一致，如果对于被求解问题没有足够的先验知识，就很难找到让决策者满意的最优解，令决策者较难有效地进行多目标决策，且还要花费较多的CPU时间开销。

（2）需要依据求解问题所需的与应用背景相关的启发式知识来设定相关的权重，不同参数的权重设置会导致产生不同的非劣解，这就要求决策者事先要对优化问题有充分的认识，能够合适地选取参数权重，而这往往是一个很难的过程。

（3）实际应用问题中不同目标的度量单位和物理意义通常不同，同时各目标之间通过决策变量相互制约，往往存在相互冲突的指标，目标之间不易直接进行比较或加权，虽可用无量纲化来量化指标以处理目标函数，但这增加了算法的复杂性，且会引起目标空间的改变，导致无法正常利用决策信息。

（4）对Pareto最优前沿形状很敏感，不能很好地处理前沿的凹部［8］，多次运行算法得到的解不能保证相互非劣等。

基于上述缺陷，这种传统的求解多目标优化问题的MOSA方法，在实际应用中受到了一定的限制。

3.3 SMOSA

Suppapitnarm等［9］设计了SMOSA算法，采用return－to－base策略，使搜索重新从解区域中的一个已归档解启动，该区域的每一对非支配解至少有一个目标彼此更优。在该算法中，每一个目标函数被指派一个不同的温度参数，在一特定的温度值时，使用可接受的解的标准偏差冷却这些参数。当达到迭代次数或者在一特定温度超过预定值时的累积记录次数，则周期性地更新这些温度参数。在搜索期间，该算法只使用一个解，且退火过程是根据每个标准的解的性能独立地调整各温度参数，归档集储存着多个目标间的所有非支配解。该方法不使用组合目标函数，而是直接与先前归档集中解相互比较每个目标的改变，这确保了接受非支配解。该文提出了一种新的接受准则：基于一个具有多个温度（一个温度对应一个目标）的冷却进度表，该接受准则不使用任何权重向量，一个新解的接受概率依赖于它是否被添加到该潜在的Pareto优化解集中，如果它被添加到该集合中，它以概率1被接受为当前解，否则，一个多目标的接受准则被使用。即如果新解未进入Pareto解集，则根据如下概率接受新解：

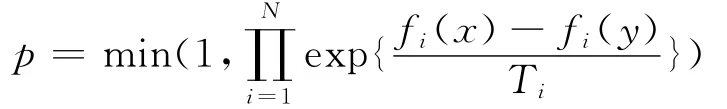
3.4 WMOSA

对于带约束的多目标优化问题，大多数MOSA算法采用一种如惩罚函数法的分离技术，而由Suman［10，11］所提出的基于权重的多目标模拟退火算法WMOSA则试图通过在接受准则中使用权重向量，直接在其主函数中处理约束。权重向量取决于解向量和目标函数向量所违背的约束个数，具体定义为：Wi＝（解向量和目标函数向量所满足的约束数＋目标函数向量的第i个元素所满足的约束数）／（与解向量和决策向量有关的约束数＋

与目标函数向量的第i个元素有关的约束数）

如果新解未进入Pareto解集，则根据如下概率接受新解：

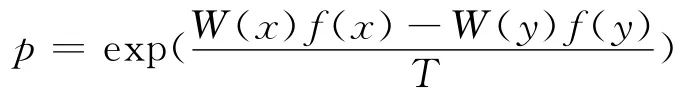
3.5 PDMOSA

Suman［11，12］设计了一种基于 Pareto支配接受准则的多目标模拟退火算法PDMOSA。在该算法中，其接受准则是基于Pareto支配的适应度值策略，它易于适应SA算法中的接受准则。PDMOSA算法的解的适应度值等于Pareto优化解集中支配该解的非劣解的个数再加1，其适应度值越小，解的质量越好。在算法搜索早期阶段，当前解和新解之间的适应度差异较小，且温度较高，任何一次移动可在两个方向上得到接受，而随着迭代次数的增加，温度下降，适应度值间的差异增大，这使得移动方位更具有选择性，从而可获得多样性良好分布的Pareto优化解集。PDMOSA没有将权重向量引入到接受准则中，惩罚函数法用来处理不可行解。PDMOSA与其他MOSA之间的主要差别：在接受准则中，没有使用目标函数值，而是使用适应度函数值，从而简化了接受概率的计算，且减少了计算时间，并使搜索逼近Pareto优化解。PDMOSA算法中接受新解的概率计算方法是：

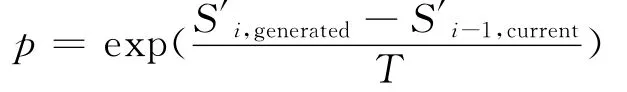
其中，S′i，generated为在第i次迭代时产生的新解基于Pareto支配的适应度值，而S′i－1，current为当前解在第i－1次迭代时当前解基于Pareto支配的适应度值。

3.6 DM－MOSA

Smith等［13］提出了一种基于支配措施的多目标模拟退火算法DM－MOSA。该算法利用一个解的相对支配关系作为系统能量进行优化，其能量函数是基于Pareto前沿的当前估计值，它表示在退火过程迄今为止找到的非支配解合并聚集之后形成的集合，并采用了三种方法（有条件地删除被支配解、线性插值和到达曲面采样）设计细粒度的能量函数。它可以促进Pareto前沿上稀疏区域的搜索能力，可消除与组合目标函数相关的一些问题。该文也提出一种为选择扰动定标因子的方法以改善搜索能力，使其对解的搜索尽量朝Pareto前沿方向迈进。该算法接受概率的计算方法是：

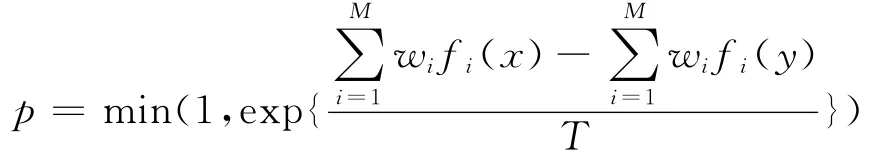
3.7 MC－MOSA

Tekinalp等人［14］在2007年提出了一种具有多种冷却进度表的多目标模拟退火算法MC－MOSA。该算法具有自适应冷却进度和使用一个适应度函数的种群以准确地生成Pareto前沿。该算法产生新解的方法是y＝x＋l，其中为服从均匀分布的单位球面上所选择的一个搜索方向，l为服从均匀分布的步长。每个适应度函数对应一个温度，每当遇到改善了的适应度函数的新解时就接受该解，同时根据适应度函数的最好值和次好值及当前解的适应度函数值冷却与改善了的适应度函数相关的温度参数。MC－MOSA算法定义了一种新的适应度函数：

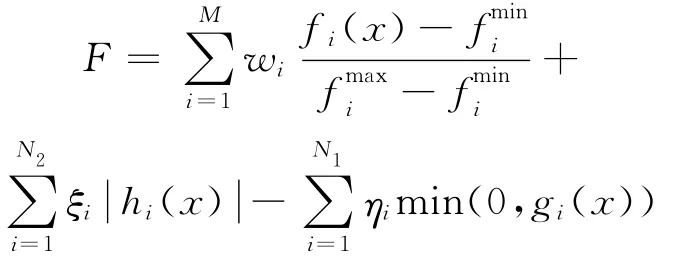
该算法的接受概率的计算方法是：

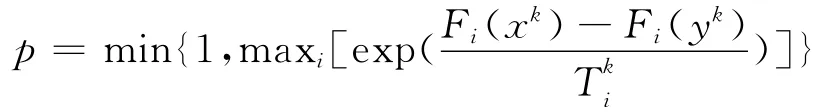
最大值，

3.8 AMOSA

归档式多目标模拟退火AMOSA是由Bandyopadhyay等人［15］于2008年提出的一种解决多目标组合优化问题的高效算法。该算法首先初始化相关参数，如初始温度等，产生初始解，计算各解的各个目标函数值，利用爬山操作和支配关系对解进行迭代提炼，将非支配解储存于归档集中，直至归档集中解的个数增至SL（SL表示对解执行聚类操作前归档集中解的最大个数）。如果归档集中解的个数超过HL（HL表示用户所需非支配解的最大个数），执行聚类操作使解的个数减至HL。其次，从归档集中随机地选择一个解作为当前解，并计算该解的多个目标函数值。在每个温度下重复执行以下过程若干次：扰动当前解产生新解，计算该解的多个目标函数值，并检测新解与当前解及归档集中解的支配关系。基于支配关系的不同，以不同概率接受新解、当前解或归档集中的某个解。若归档集中解的个数超过SL，执行聚类操作以减至HL。每个温度以一定冷却率进行退火，直至达到给定的最低温度，结束循环。

AMOSA算法分三种情况计算该算法的接受概率：（1）当 前解支配新 解，以概率p ＝设置新解为当前解；（2）新解与当前解彼此非支配，检查新解与归档集中解的支配关系，若归档集中有k（k≥1）个解支配新解，则以概率新解为当前解；（3）新解支配当前解，检查新解与归档集中解的支配关系，若归档集中有k（k≥1）个解支配新解，则以概率

置对应于Δdommin最小的那个解为当前解，否则设置新解为当前解。

3.9 rMOSA

Sankarao B等人于2011年提出了一种鲁棒的多目标模拟退火算法rMOSA［16］，它在较少的模拟次数下能收敛到Pareto解集，这些Pareto解是具有拥挤良好分布的均匀非支配解。该算法在简单MOSA算法的基础上增加了两个新的机制实施扰动以选择新解，从而具有鲁棒性。这两种机制分别是：（1）一个系统调用为执行解的扰动而在归档集中选择一个随机点，该机制的目的是加快收敛过程以获得最终Pareto前沿；（2）另一个系统调用则为执行解的扰动在归档集中选择一个最佳非拥挤解，该机制的目的是为获得具有良好拥挤分布的均匀Pareto前沿。该算法基于一个概率函数接受一个差的解，其接受概率的计算方法是：

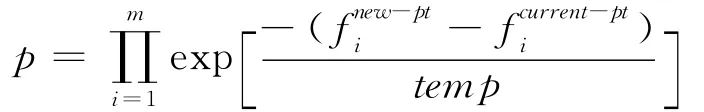
多目标优化问题的特征之一是其解往往不止一个，而是有很多个Pareto最优解，即一组在多个目标之间折衷的均衡解。解决多目标优化问题的关键是找到数量足够多且分布均匀的具有代表性的Pareto最优解组成的解集。

上述MOSA算法主要采用基于Pareto支配的方法。所谓基于Pareto支配的方法是指将多个目标值直接映射到一种基于秩的适应度函数中，通过Pareto支配关系来计算适应值。首先种群中的所有非支配解被赋予序值1，然后从种群中忽略它们，这时在种群中新的非支配解被赋予序值2，直到种群中所有解被赋予序值为止。该方法每轮运行时会考虑许多非支配解，且会储存产生的Pareto前沿的近似解，更好地反映多目标优化问题的实质，实现了真正意义上的多目标优化，不仅可以求出比单目标方法更优的解，而且通过一次优化计算可得到多个较优的Pareto最优解。

基于Pareto支配的方法是目前采用得最多的一种方法，根据Pareto最优解支配概念使用MOSA算法求解多目标优化问题时，需要解决以下两个关键问题：（1）收敛性，即解应尽快地向Pareto前沿方向进化；（2）多样性，即非劣解应尽量在Pareto前沿面上均匀分布。基于Pareto支配的MOSA算法对解的搜索方式实现了多向性和全局性，能充分利用解的多样性，使得算法能够在一次运行中获得多个Pareto最优解集。在这些MOSA中，有些使用目标函数，有些使用适应度函数值，来确定接受概率的计算公式。这些算法的主要差别在于接受准则，单目标条件下的接受准则需要进行扩展，以满足多目标优化的要求。

3.1 0 混合 MOSA

算法混合的思想已成为提高算法优化性能的一个重要而有效的途径，其出发点是使单一算法互相取长补短，产生更好的优化能力和效率，期望获得优化性能和时间性能的双赢，改善解的质量。

Baños等［17］在2007年提出了一种新颖的基于模拟退火和禁忌搜索的混合思想的多目标元启发式方法——多目标模拟退火和禁忌搜索算法，该算法使用一个多解的主种群和一个用于保存在主种群中找到的优秀解的外部归档集。在优化过程中，它合并了模拟退火算法和禁忌搜索算法，其新解的接受概率是基于解中的Pareto支配关系而决定的。

Maulik等［18］于2010年在AMOSA算法的基础上提出了一个新颖的并行版的基于粗糙集的归档式多目标模拟退火算法，该算法融合了粗糙集理论与具有归档式多目标模拟退火方法的可伸缩的分布式范式的原则。

3.1 1 其他 MOSA

Huang等人［19］于2008年在正交实验设计的基础上，利用基于Pareto支配的计分函数和多目标产生机理，提出了一种新颖的智能MOSA算法。Shu等［20］提出了一种新颖的用于解决具有大量参数的多目标优化问题的多目标正交SA算法。Li等［21］提出了一种具有自适应性和竞争性的搜索导向的进化 MOSA算法。张长林等［22］提出了一种用于求解非线性约束最优化问题的有效MOSA算法。芦金蝉等［23］利用多目标优化和物体退火之间的类比关系构建了基于SA的多目标优化算法。Bandyopadhyay［24］于 2011 年在 其 早 期 文 献［15］的基础上提出了一种具有稳定性和有效性的用于模糊聚类的MOSA算法。

4 MOSA的应用进展

目前，MOSA算法一直受到人们的广泛重视，并在诸多工程领域得到迅速推广和应用，下面列出几个典型的应用领域。

4.1 图像处理

Baños等［17］将他们所提出的 MOSATS算法用于优化图像分割问题。Saha等采用AMOSA算法对遥感卫星图像中自动像素分类［25］和卫星图像中无监督式像素分类的影像数据［26］进行多目标优化设计。在遥感卫星图象的自动像素分类中，Saha等［27］还使用 multicenter－AMOSA 算法对遥感图象数据集合同时优化以检测出适当数量的集群和恰当的分割区。

4.2 生物科学

Wang等［28］运用AMOSA算法对基因进行基于特征选择的转录起始位点的预测。刘鹏飞等［29］应用MOSA算法对非编码RNA比对及预测并行模型的多个代价函数进行优化以提高解的多样性。Lashkargir［30］等运用AMOSA算法在微阵列数据中发现基因表达数据的双向聚类，采用拥挤距离机制维持双群的多样性。

4.3 工业控制

Huang等［20］利用智能多目标模拟退火IMOSA算法解决鲁棒PID控制器的设计问题。钟爱莲［31］将AMOSA算法用于优化非相关平行机台排程问题以提供排程决策者更适合工厂现况的排程方法机制。李瑞琪［32］探讨不同策略之多目标模拟退火算法以求解非相关平行机台排程问题。Chang等［33］应用AMOSA算法对变速机调度以最大化完工时间和拖期的满意度。

4.4 机械设计

Tekinalp等［14］将所提出的具有多冷却率的MOSA算法用于运载火箭弹道的优化设计。熊庆辉等［34］采用MOSA算法实现压电堆执行器的关键结构参数全局多目标优化设计，对高压共轨喷油器的关键结构参数进行多目标仿真优化设计［35］，对高压共轨电控喷油器响应特性进行了优化设计［36］。李铁栓等［37］采用 MOSA对高压共轨电控喷油器高速电磁阀的关键结构参数进行多目标优化设计。潘金坤［38］等采用多目标模拟退火优化算法MOSA，以合模油缸推力和机构总长度为目标函数建立多目标优化设计模型，对双曲肘合模机构的关键结构参数进行多目标优化计算。熊庆辉等［39］采用多目标模拟退火优化算法，以换挡开关电磁阀的开启延迟时间、关闭延迟时间和电磁力为目标建立了多目标优化模型，对换挡开关电磁阀的主要结构参数开展多目标优化设计。

4.5 电路设计

He等［40］为设计能充分表示全功能的组合逻辑电路提出了一个多目标优化技术，该技术采用MOSA算法优化组合逻辑电路以最小化逻辑电路门的数量。Antunes等［41］采用 MOSA算法解决电力系统中无功补偿问题以优化电容器的大小和安装位置，有助于释放系统容量、提高电压等级。

4.6 网络优化

Santamaria等［42］采用 MOSA算法对时间驱动的传感器网络同时考虑多个相关性能目标进行路由优化。Smith［43］将所提出的基于优胜关系的多目标模拟退火算法用于移动通信领域中CDMA网络的优化配置。Xu等［44］提出了一个具有变邻域的进化多目标模拟退火算法以解决电信系统中多组播路由优化问题。

4.7 车间调度

Varadharajan等［45］应用 MOSA算法进行置换流水车间的调度以最小化作业的完工时间和总的流程时间。Issam等［46］使用一个基于MOSA算法的多智能系统解决静态电话预约乘车调度问题。Issam等［47］将电话预约乘车调度问题表示为一个多目标数学模型，采用MOSA算法解决动态电话预约乘车调度问题。Mokotoff［48］采用 MOSA算法解决在实际语境中置换流水车间调度问题以极小化最大完工时间和总完工时间。

4.8 其他应用领域

Kumral［49］基于 MOSA算法解决不同的有效矿物的最佳混合问题。Lucic等［50］将MOSA算法用于解决多目标空勤人员排班问题。Safaei等［51］采用MOSA算法解决一个现实的维护人力调度问题，旨在同时最大限度地降低劳动力成本和最大限度地提高设备的可用性。Ekbal等［52］采用MOSA算法，通过优化多个目标函数以解决指代消解的特征选择问题。Ekbal等［53］以基于MOSA算法的分类器集成在印第安语中的命名实体识别作为个案进行研究。

5 结束语

本文对MOSA算法及其应用进行了积极的调研，对其进展作出了一个较全面的综述。尽管在最近的二十多年已经出现了大量有关MOSA的研究工作，但相对于多目标微粒群算法、多目标遗传算法等算法的发展，MOSA算法的研究仍然是滞后的。与许多智能优化算法一样，MOSA算法的不成熟和数学基础的相对薄弱，决定了在未来相当长的时间内，仍然有许多开放性的问题值得关注和探讨，许多具有挑战性的问题亟待解决，未来的研究工作可从以下若干方面展开。

（1）冷却进度表参数的优化选取。冷却进度表是一组控制算法进程的参数，用以逼近SA算法的渐进收敛性，使算法在有限执行时间后返回一个近似最优解。冷却进度表是影响SA算法性能的重要因素，其合理选取是算法应用的关键［54］。大部分MOSA与其他SA算法一样，其求解性能依赖于一些参数的优化设置，如算法中关于初始温度、温度更新函数、内外循环终止条件等。MOSA算法对具体问题和应用环境的依赖性比较大，在不同参数及同一参数的不同取值情况下，针对不同类型的目标函数，特别是针对不同的应用问题，所得到的解是不同的。如何寻找所选各参数的不同取值的最佳组合是算法设计的一个关键方向，直接关系到所获取解的质量。至今MOSA算法的参数选择依然是一个难题，通常只能依据一定的启发式准则或大量的实验加以选取。因此，如何指导参数的优化选择，需要在理论上进行更深入的探索，将来在这方面的研究突破会极大地推进MOSA算法研究的发展。

（2）参数的自动控制。MOSA算法中涉及各种参数设置，如初始温度、冷却率等，没有确切的理论依据。MOEA参数的自动控制机制（如在线适应和自适应等，它能在无需人工干预的情况下适应性地调整其参数）的设计很少被探索［55］。因此，如何设计不用用户调整参数而使算法依据其优化进展情况适应性地调整参数的MOSA算法，使得算法既能避免早熟又能比较快速地收敛，是一个具有挑战性的问题。

（3）接受准则的设计。SA算法设计的关键是接受准则和冷却进度表，接受准则允许目标函数在有限范围内变坏，以一定概率接受新解［2］，MOSA需要对单目标条件下的接受准则进行扩展，以满足多目标优化的要求。如何设计MOSA算法的接受准则，是使用目标函数还是使用适应度函数值，抑或是采用其他参数值来确定接受概率的计算公式，值得在今后的工作中进一步摸索和探讨。

（4）终止条件的研究。终止条件包括外循环和内循环终止条件，内循环终止条件用来决定各温度下产生候选解的数目，外循环终止条件即算法终止条件，用来决定算法何时结束［56］。当前，内循环终止条件主要是按一定的步数抽样，一般可考虑算法搜索到的最优解用连续若干步的目标函数值变化较小或检验目标函数的均值是否稳定等方法来决定是否终止内循环；而外循环终止条件主要是以预先设定终止温度的阈值或最大迭代次数作为终止条件，以保证满足运算时间的要求，但却不一定能收敛到Pareto前沿。如何设计有效的算法终止准则是MOSA的一个基础理论难题之一，如何有效地证明或给出明确的算法终止准则仍是有待研究的，很难明确地判断算法迭代到一定次数已经达到了最优或者说可以终止，寻找更好的终止条件是一个亟待解决的问题。

（5）收敛性分析和证明。收敛性一直是智能优化算法研究的重点和难点，目前求解多目标问题的MOSA算法缺乏与单目标SA算法相类似的收敛性理论。从理论上分析和证明MOSA算法的收敛性，从实验方面验证MOSA算法的收敛性和收敛速度等尚没有形成通用的、完整的分析和证明方法。为此，有必要对MOSA算法的收敛性的分析和证明进行更深入的研究，提高算法的寻优能力，使得算法能更加快速、准确地寻找到全局最优解，以期为设计出性能更优的MOSA算法提供指导。

（6）解的多样性保持机制的研究。对于MOSA算法，解的多样性目前主要是通过外部归档集的维护来保证的，如文献［15］通过聚类操作来维护外部归档集以保持解的多样性。可否寻找更高效的机制提高解的多样性。这是一个值得探讨的问题。如何使算法在得到一个具有良好分布性Pareto解集的同时，也能获得一个理想的收敛性，将是今后研究工作所追求的一个重要目标，对维持解的多样性、改进所获取的解的质量等方面具有现实意义。

（7）改变算法进程的一些方法的移植。在SA算法中，改变算法进程的一些方法有回火退火法、加温退火法、多次寻优法等［54］。这些改进方法能否直接或间接移植到MOSA算法中，有待于研究者在理论上和实践中去验证。

（8）针对不同计算环境的 MOSA算法的研究。随着计算机硬件体系结构和平台技术的快速发展，如面对Cluster集群、多核CPU、GPU、Cell BE、超级计算机等不同的计算机体系结构，网格计算平台和云计算平台等不同平台技术，针对不同的计算环境对MOSA算法的性能和复杂性及其应用展开研究工作，对MOSA算法作进一步的完善也是一项有着重大应用价值和有意义的工作。

（9）并行MOSA算法的设计。随着计算技术的不断发展，算法的并行实现也越来越容易；随着并行化处理的不断深入，对并行化算法的研究也越来越普遍，并行化在算法性能提升方面的巨大潜力显而易见［57］。并行 MOSA的设计目标在于利用更少的时间、更少的计算资源或搜索更多可行解，获取比MOSA算法更多更好的优化解。对于增强MOSA算法的性能，并行技术和使用种群信息将是好的方法［58］。文献［54］讨论了SA算法的并行实现方法和形式，文献［59］提出了一种并行SA算法。那么，对于MOSA算法，能否移植并行单目标SA算法的思想来构建并行MOSA算法，MOSA算法的并行实现的可能性和途径、并行策略及在并行领域的实际应用，值得在今后的工作中进一步探讨。Maulik等［18］于2010年在AMOSA算法的基础上提出了一个新颖的并行版的基于粗糙集的AMOSA算法，这为并行化MOSA提供了可鉴思路。因此，寻找有效并行技术和性能度量方法是未来的工作，实现MOSA算法的并行化，让算法在分布（并行）的计算环境中运行显然是一种有意义的值得期待的尝试。

（10）基于MapReduce的并行MOSA算法的设计。MapReduce［60］框架是Google提出的一种处理超大规模数据集的新型分布式并行编程模型，采用了“分而治之”的思想。Monte Carlo是一种随机模拟和不确定性方法，是一种可以有效实现并行计算的算法结构，任何一个属于Monte Carlo方法的应用都可以运行在云计算环境中。MOSA是一种基于Monte Carlo迭代求解策略的启发式随机优化算法，而Monte Carlo方法又是一种典型可并行化的方法，且MapReduce是目前云计算的核心计算模式。基于此，我们可以采用MapReduce技术，设计云计算环境下的基于MapReduce的并行MOSA算法，这在云计算时代具有很好的应用前景。

（11）动态MOSA算法的设计。对于动态环境优化问题，在其求解的过程中，它的决策参数、目标函数值、约束条件等都可能发生变化，目前国内外相关的研究文献相对比较少。对于动态优化进化算法，大多还是集中在如何得到尽可能满足问题条件的最优解或近似最优解，对算法的有效性、收敛性及解的质量等考虑的较少［61］。因此，如何设计动态MOSA算法，使算法尽可能有效地跟踪动态多目标优化问题随时间（环境）发生变化的Pareto最优解，使算法在动态变化的环境下能求得质量较好、数量较多、分布较广且均匀的Pareto最优解，以及在求解过程中如何动态调整MOSA的一些参数，以自适应求解动态环境下的优化问题，这是一个挑战。

（12）基于新型占优机制的 MOSA算法的设计。很多学者开始注意到Pareto占优的局限性，如何引入新的占优机制以有效解决高维多目标优化问题成为进化多目标优化研究者接下来的主要任务之一［55］。将新型占优机制，如ε－占优的档案更新策略［63］引入到MOSA中，并应用其解决多目标优化问题，且通过理论和结合实际多目标优化问题验证算法解决实际问题的可行性，有效性等。

（13）混合MOSA算法的设计。单纯依赖一种算法求解复杂优化问题，有时效果并不好，与其他算法进行混合是提高算法优化性能的一个重要且有效的途径，不同算法的相互补充、融合已被证明是一种有效地改良方式。MOSA作为一种多目标智能优化算法，与其他算法融合和比较的研究仍处于初级阶段，相关的研究文献和报告较少。MOSA具有大范围快速全局搜索能力，但对系统中的反馈信息利用不够，当求解到一定范围时往往做大量无为的冗余迭代，求精确解效率降低，若能在MOSA中融合蚁群算法思想找邻域解，可能效果会更好，如在MOSA中融合禁忌搜索算法以避免算法迂回搜索、采用微粒群算法为MOSA提供初始解等，进一步改善 MOSA的性能，以及探讨MOSA与其他算法之间的联系都是非常有意义的研究方向。因此，寻求MOSA算法的弱点，充分利用其它算法的优势，取长补短，基于算法统一框架，发展高效的混合MOSA算法，已成为人们关注的热点。

（14）其他新颖的MOSA算法的设计。针对搜索全局性、快速性和鲁棒性，根据现有多目标优化方法所采用的思想和技术（拥挤距离、聚类、混沌、模糊集等），引入新的优化机制和操作，如在MOSA中引入偏好排序代替Pareto支配排序、采用新的存档策略等，设计出新颖的MOSA算法，通过理论和实践证明其优越性和不足之处，并不断完善这将是一个令人期待和极富挑战的研究领域。

（15）与其他多目标智能优化算法的比对研究。新型的算法结构或混合算法对算法性能和效率有较大幅度的改善。结合实际应用或理论问题对算法进行对比研究也是算法研究中值得关注的内容。它有助于分析算法的性能和适用域，且由比较可发现各算法独特的优点和不足，来改进结构或操作或参数，发展各种可能的高效混合算法［56］。因此，将MOSA算法与其他多目标智能优化算法进行比对研究，以进一步完善算法。

（16）拓展 MOSA算法的应用领域。MOSA是一种新颖的多目标优化算法，可用于解决大多数多目标优化问题，虽已被应用到一些领域，但远没有其他多目标智能优化算法（如多目标微粒群算法、多目标遗传算法等）应用广泛。因此，拓宽MOSA算法在实际工程问题中的应用，如交通与物流系统优化、多播QoS路由优化、Web服务组合、数据挖掘等领域，将是MOSA算法应用研究中值得重视的有实际价值的课题。将MOSA算法用于解决更多的实际问题，验证算法的适用性和有效性，进一步进行更广泛更深入的应用研究，再根据应用的反馈信息，改进和完善现有算法的性能，从而达到算法理论与实际应用相互促进的目的，这仍旧是一个开放问题。

总之，未来在设计或改进MOSA算法时要同时注意：算法应具有较快的收敛速度，所得的最优解要尽可能接近Pareto前沿、尽可能宽广均匀地分布在Pareto前沿，并且尽可能将其用于解决实际应用问题等。

［1］ Kirkpatrick S，Gerlatt C D，Vecchi M P.Optimization by simulated annealing［J］.Science，1983，220（4598）：671－680.

［2］ Lei De－ming，Yan Xin－ping.Multi－objective intelligent optimization algorithm and its application［M］.Beijing：Science Press，2009.（in Chinese）

［3］ Suman B，Kumar P.A survey of simulated annealing as a tool for single and multi－objective optimization［J］.Journal of

the Operational Research Society，2006，57：1143－1160.

［4］ Ulungu E L，Teghem J，Ost C.Interactive simulated annealing in a multi－objective framework：Application to an industrial problem［J］.Journal of the Operational Research Society，1998，49：1044－1050.

［5］ Ulungu E L，Teghem J，Fortmeps P H，et al.MOSA method：A Tool for solving multi－objective combinatorial optimization problems［J］.Journal of Multi－Criteria Decision Analysis，1999（8）：221－236.

［6］ Haidine A，Lehnert R.Multi－case multi－objective simulated annealing（MC－MOSA）：New approach for adapt simulated annealing to multi－objective ptimization［EB／OL］.［2012－05－16］.http：／／www.akademik.unsri.ac.id／download／journal／files／waset／v4－3－28－6.pdf.

［7］ Czyzak P，Jaszkiewicz A.Pareto simulated annealing－a meta－heuristic technique for multiple－objective combinatorial optimization［J］.Journal of Multi－Criteria Decision Analysis，1998（7）：34－47.

［8］ Cui Xun－xue.Multi－objective evolutionary algorithm and its application［M］.Beijing：National Defense Industry Press，2008.（in Chinese）

［9］ Suppapitnarm A，Seffen K A，Parks G T.Simulated annealing：An alternative approach to true multi－objective optimization［J］.Engineering Optimization，2000，33（1）：59－85.

［10］ Suman B.Multi－objective simulated annealing—a meta－heuristic technique for multi－objective optimization of a constrained problem［J］.Foundations of Computing and Decision Sciences，2002，27（3）：171－191.

［11］ Suman B.Simulated annealing－based multi－objective algorithms and their application for system reliability［J］.Engineering Optimization，2003，35（4）：391－416.

［12］ Suman B.Study of simulated annealing based algorithms for

multi－objective optimization of a constrained problem［J］.

Computers ＆ Chemical Engineering，2004，28：1849－1871.［13］ Smith K I，Everson R M，Fieldsend J E，et al.Dominance measures for multi－objective simulated annealing［C］∥Proc of Congress on Evolutionary Computation（CEC2004），2004：23－30.

［14］ Tekinalp O，Karsli G.A new multi－objective simulated annealing algorithm ［J］.Journal of Global Optimization，2007，39（1）：49－77.

［15］ Bandyopadhyay S，Saha S，Maulik U，et al.A simulated annealing based multi－objective optimization algorithm：AMOSA［J］.IEEE Transactions on Evolutionary Computation，2008，12（3）：269－283.

［16］ Sankara O B，Chang K Y.Development of a robust multiobjective simulated annealing algorithm for solving multiobjective optimization problems［J］.Industrial ＆ Engineering Chemistry Research，2011，50（11）：6728－6742.

［17］ Baños R，Gil C，Paechter B，et al.A hybrid meta－heuristic for multi－objective optimization：MOSATS［J］.Journal of Mathematical Modeling and Algorithms，2007，6（2）：213－230.

［18］ Maulik U，Sarkar A.Evolutionary rough parallel multi－objective optimization algorithm［J］.Fundamenta Informaticae，2010，99（1）：13－27.

［19］ Huang M H，Shu L S，Ho S J，et al.A novel intelligent multi－objective simulated annealing algorithm for designing robust PID controllers［J］.IEEE Transactions on Systems，Man，and Cybernetics—Part A：Systems and Humans，2008，38（2）：319－329.

［20］ Shu L S，Ho S J，Ho S Y，et al.A novel multi－objective orthogonal simulated annealing algorithm for solving multiobjective optimization problems with a large number of parameters［EB／OL］.［2012－05－15］.http：／／www.springerlink.com／index／ULJ9BFAGK6U1N0LC.pdf.

［21］ Li H，Landa－silva D.Evolutionary multi－objective simulated annealing with adaptive and competitive search direction［EB／OL］.［2012－05－18］.http：／／www.cs.nott.ac.uk／～jds／research／files／jdls＿cec2008.pdf.

［22］ Zhang Chang－lin，Yu Jian－xing，Yang Zhen－guo.The multiobject simulated annealing algorithm for the nonlinear constraint optimization problem［J］.Journal of Fudan University：Natural Science，2003，42（1）：93－97.（in Chinese）

［23］ Lu Jin－chan，Li Nai－cheng，Wang Wei－dong.Multi－objective optimization approach based on simulated annealing［J］.Computer Engineering and Applications，2003（23）：92－94.（in Chinese）

［24］ Bandyopadhyay S.Multi－objective simulated annealing for fuzzy clustering with stability and validity［J］.IEEE Transactions on Systems，Man and Cybernetics－Part C：Applications and Reviews，2011，41（5）：682－691.

［25］ Saha S，Bandyopadhyay S.Use of different forms of symmetry and multi－objective optimization for automatic pixel classification in remote－sensing satellite imagery［J］.International Journal of Remote Sensing，2010，31（22）：5751－5775.

［26］ Saha S，Bandyopadhyay S.Unsupervised pixel classification in satellite imagery using a new multi－objective symmetry based clustering approach［C］／／Proc of the IEEE TENCON，2008：1－6.

［27］ Saha S，Bandyopadhyay S.Automatic pixel classification in remote sensing satellite imagery using a new multi－objective simulated annealing based clustering technique［C］∥Proc of Seminar on Spatial Information Retrieval，Analysis，Reasoning and Modelling，2009：98－118.

［28］ Wang X，Bandyopadhyay S，Xuan Z，et al.Prediction of transcription start sites based on feature selection using AMOSA［C］∥Proc of Computational Systems Bioinformatics Conference，2007：183－193.

［29］ Liu Peng－fei，Dong Shou－bin，Cao Yi－cheng，et al.Alignment and prediction of multi－objective optimized non－coding RNA［J］.Computer Engineering，2009，35（9）：225－226.（in Chinese）

［30］ Lashkargir M，Tabatabaeifar M S，Taghizadeh S.An archived multi－objective simulated annealing method to discover biclusters in microarray data［J］.International Journal on Advanced Science，Engineering and Information Technology，2011，1（3）：257－261.

［31］ Jhong Ai－lian.Archive－based optimization heuristics for fuzzy multi－objective unrelated parallel machine scheduling problems［D］.Taiwan：Yuan Ze University，2009.（in Chinese）

［32］ Li Ruei－chi.Applying simulated annealing with matching improvement to solve fuzzy multi－objective unrelated parallel machine scheduling problems［D］.Taiwan：Yuan Ze U－niversity，2010.（in Chinese）

［33］ Chang Wei－shung，Chyu Chiuh－cheng，Li Ruei－chi.Archived simulated annealing for unrelated parallel machine scheduling to maximize satisfactions of makespan and tardiness［EB／OL］.［2012－05－18］.http：／／apiems.net／archive／apiems2010／pdf／AI／88.pdf.

［34］ Xiong Qing－hui，ZhangYou－tong，Su Hai－feng，et al.Simulation research of the multilayer piezoelectric stack actuator based on the MOSA algorithm［J］.Small Internal Combustion Engine and Motorcycle，2011，40（1）：6－10.（in Chinese）

［35］ Xiong Qing－hui，Zhang You－tong.Multi optimization simulation design of a high pressure common rail injector based on MOSA algorithm［J］.Transactions of the Chinese Society for Agricultural Machinery，2011，42（1）：27－30.（in Chinese）

［36］ Xiong Qing－hui，Zhang You－tong，Wang Ding－biao，et al.Multi－objective optimizing simulation research of common rail injector ［J］.Journal of System Simulation，2011，23（6）：1137－1140.（in Chinese）

［37］ Li Tie－shuan，Zhang You－tong，Wang Ding－biao，et al.Optimization design of high－speed solenoid based on multi－objective simulated annealing method［J］.Vehicle Engine，2010（4）：6－10.（in Chinese）

［38］ Pan Jin－kun，Wang Xian－min.Multi－Objective optimization on the joint－double clamping unit［J］.Journal of Mechanical Transmission，2012，35（10）：81－85.（in Chinese）

［39］ Xiong Qing－hui，Gu Hong－tao，Li Juan，et al.Multi－objectives optimization design on the on－off shift solenoid of integrated transmission ［J］.Vehicle ＆ Power Technology，2012（3）：1－4.（in Chinese）

［40］ He Guo－liang，Li Yuan－xiang，Wang Xuan，et al.Multiobjective simulated annealing for design of combinational logic circuits［C］∥Proc of the 6th World Congress on Intelligent Control and Automation （WCICA），2006：3481－3484.

［41］ Antunes C H，Lima P，Oliveira E，et al.A multi－objective simulated annealing approach to reactive power compensation［J］.Engineering Optimization，2011，43（10）：1063－1077.

［42］ Santamaria M L，Galmes S.Multi－objective simulated an－nealing approach for optimal routing in time－driven sensor networks［C］∥Proc of the 19th Annual IEEE International Symposium on Modeling，Analysis，and Simulation of Computer and Telecommunication Systems，2011：45－461.

［43］ Smith K I.A study of simulated annealing techniques for multi－objective optimization［EB／OL］.［2012－05－15］.https：／／eric.exeter.ac.uk／repository／bitstream／handle／10036／3176／ksmith＿thesis.pdf？sequence＝1.

［44］ Xu Y，Qu R.Solving multi－objective multicast routing problems by evolutionary multi－objective simulated annealing algorithms with variable neighborhoods［J］.Journal of the Operational Research Society，2011，62：313－325.

［45］ Varadharajan T K，Rajendran C.A multi－objective simulated－annealing algorithm for scheduling in flowshops to minimize the makespan and total flowtime of jobs［J］.European Journal of Operational Research，2005，167（3）：772－795.

［46］ Issam Z，Kamel Z，Khaled M，et al.A multi－agent system based on the multi－objective simulated annealing algorithm for the static dial a ride problem［C］∥Proc of the 18th World Congress of the International Federation of Automatic Control（IFAC），2011：2172－2177.

［47］ Issam Z，Khaled M，Kamel Z，et al.A new approach based on the multi－objective simulated annealing to solving the dynamic dial a ride problem［C］∥Proc of the 4th International Conference on Logistics（LOGISTIQUA’2011），2011：157－163.

［48］ Mokotoff E.Multi－objective simulated annealing for permutation flow shop problems［J］.Computational Intelligence in Flow Shop and Job Shop Scheduling，2009：101－150.

［49］ Kumral M.Application of chance－constrained programming based on multi－objective simulated annealing to solve a mineral blending problem［J］.Engineering Optimization，2003，35（6）：661－673.

［50］ Lucic P，Teodorovic D.Simulated annealing for the multiobjective aircrew rostering problem［EB／OL］.［2012－05－16］.http：／／filebox.vt.edu／users／duteodor／P%2034.pdf.

［51］ Safaei N，Banjevic D，Jardine A K S.Multi－objective simulated annealing for a maintenance workforce scheduling problem：A case study［EB／OL］.［2012－05－18］.http：／／delta.cs.cinvestav.mx／～ccoello／EMOO／safaei08.pdf.gz.

［52］ Ekbal A，Saha S，Uryupina O，et al.Multi－objective simulated annealing based approach for feature selection in anaphora resolution［C］∥Proc of DAARC’11，2011：47－58.

［53］ Ekbal A，Saha S.A multi－objective simulated annealing approach for classifier ensemble：Named entity recognition in Indian languages as case studies［J］.Expert Systems with Applications，2011，38（12）：14760－14772.

［54］ Kang Li－shan，Xie Yun，You Shi－yong，et al.Non－numerical parallel algorithm （The first volume）：Simulated annealing algorithm ［M］.Beijing：Science Press，1994.（in Chinese）

［55］ Coello C A C.Evolutionary multi－objective optimization：Some current research trends and topics that remain to be explored［J］.Fronters Computer Science in China，2009，3（1）：18－30.

［56］ Wang Ling.Intelligent optimization algorithm and its application［M］.Beijing：Tsinghua University Press，2003.（in Chinese）

［57］ Yang Hai－jun，Li Jian－wu，Li Min－qiang.Study on the pattern emergence and the difficulty of the evolutionary algorithm［M］.Beijing：Science Press，2012.（in Chinese）

［58］ Nam D K，Park C H.Multi－objective simulated annealing：A comparative study to evolutionary algorithms［EB／OL］.［2012－05－15］.http：／／citeseerx.ist.psu.edu／viewdoc／download？doi＝10.1.1.74.2194＆rep＝rep1＆type＝pdf.

［59］ Su C T，Hsu C M.Multi－objective machine－part cell formation through parallel simulated annealing［J］.International Journal of Production Research，1998，36（8）：2185－2207.

［60］ Dean J，Ghemawat S.MapReduce：Simplified data processing on large clusters［J］.Communications of the ACM，2008，51（1）：107－113.

［61］ Liu Chun－an.Dynamic multi－objective optimization evolutionary algorithm and its application［M］.Beijing：Science Press，2011.（in Chinese）

［62］ Jiao Li－cheng，Shang Rong－hua，Ma Wen－ping，et al.Multiobjective optimization immune algorithm，theory and application［M］.Beijing：Science Press，2010.（in Chinese）

［63］ Zheng Xiang－wei，Liu Hong.A cooperative co－evolutionary andε－dominance based MOPSO［J］.Journal of Software，2007，18（Suppl）：109－119.（in Chinese）

附中文参考文献：

［2］ 雷德明，严新平.多目标智能优化算法及其应用［M］.北京：科学出版社，2009.

［8］ 崔逊学.多目标进化算法及其应用［M］.北京：国防工业出版社，2008.

［22］ 张长林，余建星，杨振国.非线性约束最优化问题的多目标模拟退火算法［J］.复旦学报：自然科学版，2003，42（1）：93－97.

［23］ 芦金婵，李乃成，王伟东.基于模拟退火的多目标优化算法［J］.计算机工程与应用，2003（23）：92－94.

［29］ 刘鹏飞，董守斌，曹以诚，等.多目标优化的非编码RNA比对及预测 ［J］.计算机工程，2009，35（9）：225－226.

［31］ 钟爱莲.模糊多目标非相关平行机台排程问题之解算［D］.台湾：元智大学，2009.

［32］ 李瑞琪.模拟退火结合配对机制求解多目标非相关平行机台排程问题［D］.台湾：元智大学，2010.

［34］ 熊庆辉，张幽彤，苏海峰，等.基于 MOSA算法的压电堆执行器多目标优化仿真研究 ［J］.小型内燃机与摩托车，2011，40（1）：6－10.

［35］ 熊庆辉，张幽彤.基于MOSA算法的高压共轨喷油器多目标仿真优化设计 ［J］.农业机械学报，2011，42（1）：27－30.

［36］ 熊庆辉，张幽彤，王定标，等.高压共轨喷油器多目标优化仿真研究 ［J］.系统仿真学报，2011，23（6）：1137－1140.

［37］ 李铁栓，张幽彤，王定标，等.基于多目标模拟退火算法的高速电磁阀优化设计［J］.车用发动机，2010（4）：6－10.

［38］ 潘金坤，王贤民.双曲肘合模机构的多目标优化设计［J］.机械传动，2012，35（10）：81－85.

［39］ 熊庆辉，顾宏，李娟，等.综合传动装置换挡开关电磁阀多目标优化设计［J］.车辆与动力技术，2012（3）：1－4.

［54］ 康立山，谢云，尤矢勇，等.非数值并行算法（第一册）：模拟退火算法［M］.北京：科学出版社，1994.

［56］ 王凌.智能优化算法及其应用［M］.北京：清华大学出版社，2003.

［57］ 杨海军，李建武，李敏强.进化算法的模式涌现与困难性研究［M］.北京：科学出版社，2012.

［61］ 刘淳安.动态多目标优化进化算法及其应用［M］.北京：科学出版社，2011.

［62］ 焦李成，尚荣华，马文萍，等.多目标优化免疫算法、理论和应用［M］.北京：科学出版社，2010.

［63］ 郑向伟，刘 弘.一种基于合作型协同和ε－占优的多目标微粒群算法［J］.软件学报，2007，18（Suppl）：109－119.