主元分析法在MIMO 系统中的故障检测与诊断研究❋

曹立学

（陕西理工学院 电气工程学院，陕西 汉中 723003）

0 引言

在连续生产过程系统中，不可避免地会出现局部控制回路发生故障，或某些环节失效，都会导致产品质量下降，能耗上升，甚至会使厂级控制系统瘫痪，发生安全事故，所以系统的故障检测与诊断是系统安全运行的重要一环。另外，过程控制系统一般都具有建模困难、过程参数众多，并且各个参数之间存在相互关联相互影响的现象，由于复杂工业过程中存在着各种随机干扰因素，此时机理分析诊断方法则很难应用于现实，而多元统计分析方法是一种不依赖于过程内在机理的建模方法，它只需要根据过程相关数据信息进行统计建模，再根据该统计模型完成过程的检测与诊断。

本文应用主元分析法（Principal Component Analysis，PCA）对多输入多输出（MIMO）控制系统中的故障进行检测与诊断，为系统实现容错控制及安全运行提供保障。

1 主元分析基本理论

主元分析法主要是通过将采集到的高维信息投影到低维子空间，并保留主要变化信息及特征，再从新数据信息中提取相应要求的主元，来简化数据的分析复杂程度。

设多变量数据矩阵为X∈Rm×n，每一列对应一个参数变量，每一行对应一个数据样本。对Xm×n进行标准化后的数据矩阵为X＊，对矩阵X＊可进行奇异值分解，分解后为m个向量的外积之和，即：

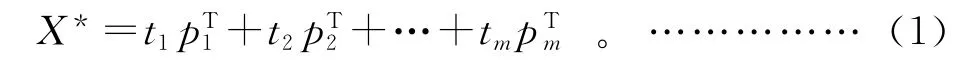
其中：ti（i＝1，2，3，…，m）称作得分向量，也称为 X＊的主元，用来提取采样数据之间的相关联信息；pi是主元的特征向量，也称负荷向量，主要用来提取参数之间的关联信息。若假设：

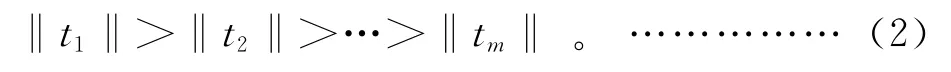
则式（1）进一步可写为：

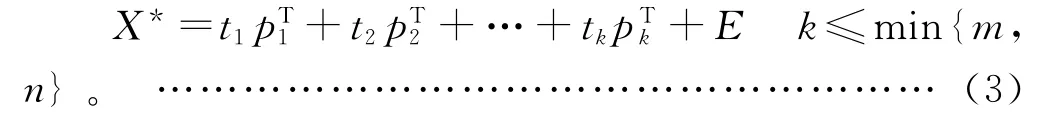
其中：E为误差矩阵，是X＊后面比较小的负荷向量，用以提取随机噪声和模型误差信息，一般可以略去。此时负荷向量p1代表X＊变化的最大方向，依次类推。各个得分向量之间是正交的，即对任何i和j，当i≠j时，满足tTitj＝0。各个负荷向量之间也是正交的，且每个负荷向量的长度都是1，即：

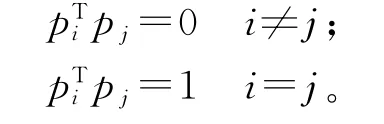
合理选取主元的个数非常重要。主元个数选取的多则能接近真实模型，得到的结果相对比较精确，但这样会增加分析与判断的复杂性，无法有效消除噪声的影响；若主元个数选取过少，就不会充分反映原始数据信息中的主要内容，相当于人为增加了分析误差。在实际应用中，一般采用贡献率累积方差百分比（Cumulative Percent Variance，CPV）法、能量百分比法或交叉检验法。本文主要采用累积和百分比法进行主元的选取。

2 统计过程控制图

2．1 诊断模型的建立

CPA统计分析是把过程的数据向量垂直投影于两正交的主元空间和误差空间上，并对其相对应的统计信息进行假设检验，用来判断过程的运行情况。主要运用多变量统计过程控制图，一般有主元得分图、Hotelling T2图、贡献图、平方预测误差SPE图。

2．2 统计控制图

建立CPA模型后一般用SPE图和Hotelling T2图进行过程监测。看生产过程的实时数据是否处于平方预测误差SPE和Hotelling T2的控制限之下，若超出控制限，则表示出现异常状况。

2．2．1 Hotelling T2图

Hotelling T2图表示的是得分向量的标准平方和，它说明了每个数据样本在变化趋势和幅度上偏离真实模型的程度大小。第k时刻主元模型的T2统计量定义为：

其中：ti（k）为得分向量ti的第k 行值为ti的估计方差。T2统计量的控制限可利用F分布按下式进行计算：

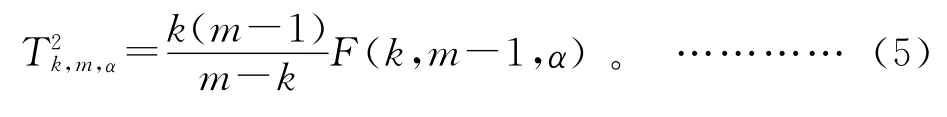
其中：m为样本个数；k为保留的主元个数；F（k，m－1，α）为置信度为α、自由度为（k，m－1）条件时的F分布的上限值。若T2＞则表明过程出现异常情况。

基于Hotelling T2的假设判断只能用在主元子空间中某些变量的变化，如果存在测量的参数没有被体现在主元模型中，则这个参数的故障也就不能通过Hotelling T2图进行检测。

2．2．2 SPE图

统计量平方预测误差（SPE）在i时刻的值是标量，它说明此时刻测量值对主元模型的偏离大小，表明从一个采样样本点到模型空间的距离。SPE统计量也被称为Q统计量。主元模型对第i个样本的平方预测误差可写为：

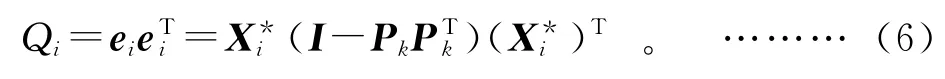
其中：ei为误差矩阵E 的第i行；Pk＝［p1p2…pk］；I为单位阵。SPE统计量反映数据当中没有被主元模型能够解释的变化，若SPE太大则说明过程出现了异常情况。

当检验水平为α时，其SPE的控制限可根据下式来计算：

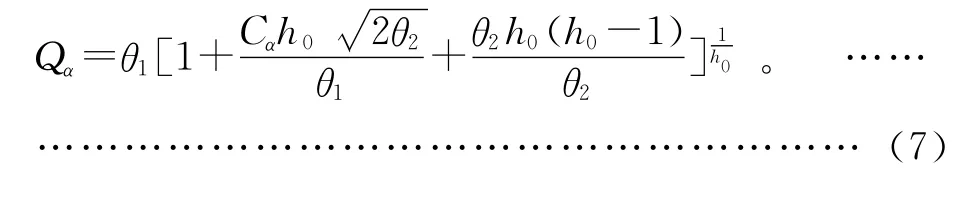
其中：θj＝为X＊协方差矩阵的特征值；h0＝1为置信度为α时的正态分布的临界值。如果统计结果Q＜Qα，说明此时的SPE统计正常。

2．2．3 主元得分图

主元得分图反映了主元模型内部各个主元素跟随时间变化的情况，其得分向量可用式ti＝X＊pi来计算。同样主元得分向量的控制限为：

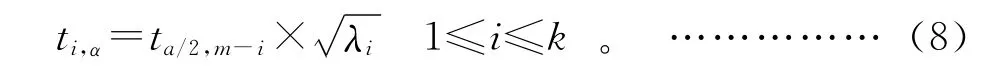
其中：ti，α为置信度为α 的得分向量。如果ti＞ti，α，则说明此时刻主元得分分析异常；否则，说明统计正常。

2．2．4 贡献图

当Q统计量或T2统计量超过其控制极限时，则说明过程中可能出现了异常，但结果并不能从Q统计图或Hotelling T2图中找出发生的故障，必须借助贡献图来确定故障源的位置。第i个过程变量对在第k时刻的Q统计量的贡献可表示为：

3 应用

本文以某2I2O液位控制系统为例，该液位控制系统的流程图如图1所示。系统要求对两个水箱的液位h1、h2进行定值控制，1＃水箱被控变量用LT1测量，通过u1控制流量q1，2＃水箱用LT2进行测量，通过u2控制流量q2。两容器之间通过阀门有相互关联，关联系数为f0，另外，两个水箱的自泄流分别为d1、d2。

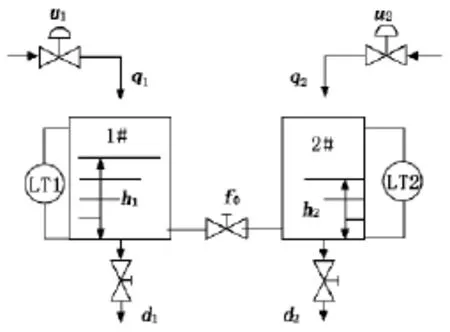
图1 2I2O液位控制系统示意图

采用PCA的分析设计方法，分别对LT1、LT2的测量量及u1、q1、u2、q2、f0等7个变量进行检测。系统在正常运行一些时间后可以进行故障测试，分别取正常运行阶段和故障阶段的数据并建立模型，得出相应主元的贡献率，确定主元个数为2，并分别计算统计指标SPE、Hotelling T2、主元负荷向量及得分向量，确定其置信度为95%时的控制限分别为：Qα＝0．275 2（95%），＝7．762（95%）。

图2和图3分别给出了SPE统计量图和Hotelling T2统计图。由图2和图3可以看出：系统在前面时间运行正常，而到后半阶段出现了样本数据超出控制限情况，说明该阶段样本出现了异常，系统有某部分出现了故障。通过对得分向量图进行分析比较，发现第1个主元得分向量没有测量点偏移，而第2个主元得分向量图中后半阶段有多个测量点超过置信限，再通过观察第2主元负荷向量图发现第5和第6两个变量对第2主元贡献率最大，而这两个变量又是控制第2个容器的液位大小的进料情况，由此可判断是第2个控制回路出现故障，经查验是第2个调节阀出现故障，开度幅度超出系统要求。

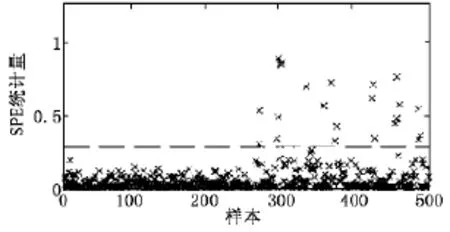
图2 SPE统计量图

4 结论

采用主元分析（PCA）法依据多输入多输出系统的原始复杂数据信息，实现对复杂数据信息的特征提取，并构建了相应过程的主元模型。主元模型丢弃了部分误差而保留能体现数据变化的主要方向，通过检验新的数据样本对于主元模型的偏离程度来发现异常和故障。仿真结果与实际运行表明，多变量统计过程能够根据过程的变化做出判断，从而达到检测与诊断的目的，提高系统的安全可靠性。

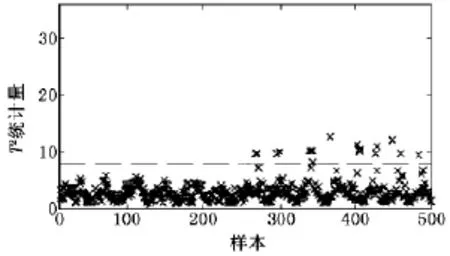
图3 Hotelling T2统计图

［1］ 李果，张鹏，李学仁，等．基于动态主元分析法的传感器故障检测［J］．数据采集与处理，2008，23（3）：238－241．

［2］ 皇金锋．升降压型开关变换器建模与控制［J］．电源技术，2011（7）：850－852．

［3］ 令朝霞．一类多输入多输出系统的容错控制设计［J］．陕西理工学院学报（自然科学版），2011（2）：24－28．

［4］ 杨瑞明．基于主元分析的生产过程质量控制与诊断［J］．制造业自动化，2012（16）：81－83．

［5］ 张鹏军，薄玉成，王惠元，等．基于小波和PCA的火炮输弹系统故障诊断研究［J］．计算机工程与设计，2012（12）：4746－4750．

［6］ 郭小芳，李锋，叶华．基于主元的多元时间序列聚类分析方法研究［J］．测控技术，2012（12）：104－107．