基于粒子群算法的磁悬浮储能飞轮结构优化设计❋

王 喆，谭天力，周 双，徐开发，安宏彬

（武汉理工大学 机电工程学院，湖北 武汉 430070）

0 引言

在磁悬浮飞轮储能系统中，飞轮是系统储能性能的核心部件［1］，通常希望它能以尽可能小的质量来储存尽可能多的能量，即要有高的储能密度，而在设计转速下飞轮的储能密度主要取决于飞轮的结构形状。近年来国内外学者对飞轮的结构作了很多的设计研究。Arslan［2］基于有限元法研究了6种不同截面形状的金属飞轮的储能性能。Eby等［3］采用并行遗传算法研究变厚金属飞轮的储能密度最大化问题，但这些算法需要人为确定较多参数，并且收敛速度慢，效率不高。郭振宇等［4］采用差异演化算法对飞轮结构进行了优化，此算法采用了迭代离散控制点的优化思路，计算繁琐，耗时长，且易陷入局部最优解。本文在已有研究成果的基础上，运用粒子群优化算法，并结合ANSYS有限元分析软件，对磁悬浮储能金属飞轮进行了结构优化设计。

1 磁悬浮飞轮储能原理

磁悬浮飞轮储能装置是通过外部动力源带动基于磁悬浮技术支承的飞轮高速旋转，能量以飞轮的机械能形式储存，然后通过发电机将机械能转换为电能输出。本文中的飞轮样机如图1所示，磁悬浮支承结构如图2所示，采用永磁轴承和机械轴承相结合，保证飞轮在较高转速下稳定旋转。

2 飞轮结构优化的数学模型

2．1 目标函数

对于材料均匀、厚度可变的金属飞轮，设飞轮的轴向厚度δ（r）是半径r的函数，则飞轮的质量m、转动惯量J和动能E可分别表示为：

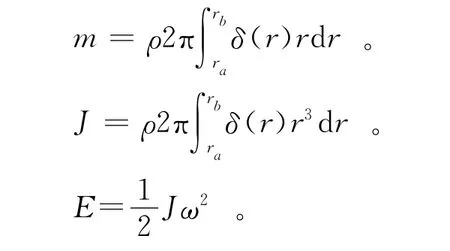
其中：ρ为飞轮材料密度；ω为飞轮转速；ra、rb分别为飞轮内、外径。

图1 飞轮样机

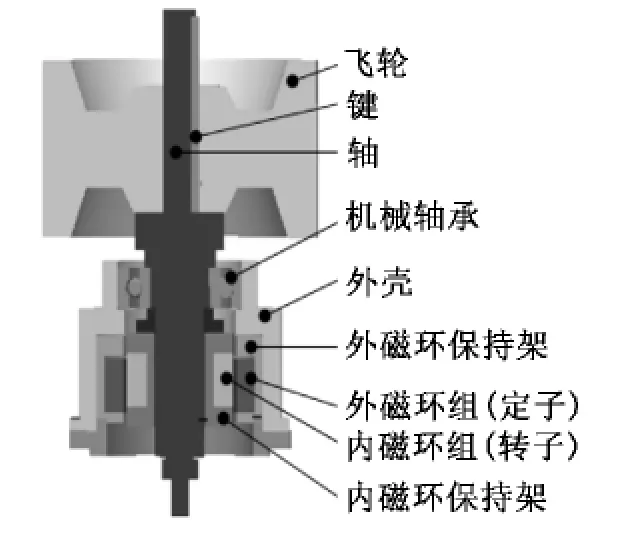
图2 磁悬浮支承结构

单位质量飞轮储存的能量为飞轮的储能密度，则飞轮的储能密度D表示为：

其中：R为飞轮的有效回转半径。飞轮的储能密度是衡量飞轮储能性能的重要指标，本文以此作为结构优化模型的目标函数。由式（1）可知，提高飞轮转速和增大飞轮的有效回转半径都可以增大飞轮的储能密度，在材料确定的情况下，飞轮的转速要受到飞轮材料强度的限制。因此在给定设计转速下，飞轮的储能密度主要取决于飞轮的结构形状。

2．2 约束条件

（1）基于磁悬浮支承的飞轮高速旋转时主要承受离心力作用，可以采用平面应力理论来分析飞轮受力情况［5］。由平衡条件［6］知：

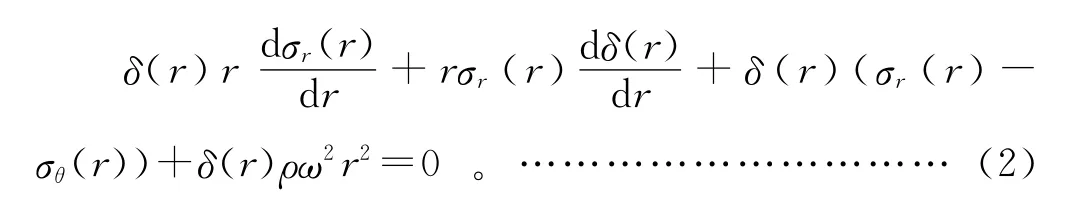
其中：σθ为环向应力；σr为径向应力。

本构方程为：

其中：εθ、εr分别为环向应变和径向应变；μ为泊松比。

几何方程为：

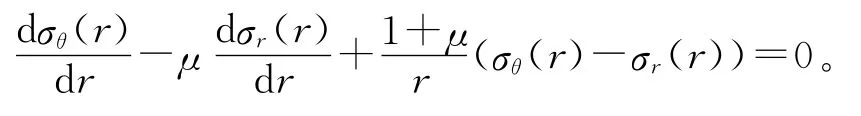
在离心力作用下，飞轮在平面应力场中径向应力和环向应力都是受拉的，所以σθ（r）＞0，σr（r）≥0，则依据Tresca准则有：

σθ（r）≤［σ］，σr（r）≤［σ］。

（2）为满足装配要求，飞轮的设计还应满足尺寸要求：

δmin≤δ（r）≤δmax。

其中：δmin、δmax分别为飞轮最小、最大轴向厚度。

2．3 优化模型

对于本文样机中的飞轮，材料选用普通碳钢Q235，其密度ρ＝7．8×103kg／m3，屈服强度σs＝235 MPa，泊松比μ＝0．26；δmin＝30mm，δmax＝80mm；在内径ra处的边界条件是：σr（ra）＝0，ra＝9mm。因此，

其中：u为径向位移。

由式（2）～式（5）可得应力协调方程为：飞轮结构优化模型可描述为：

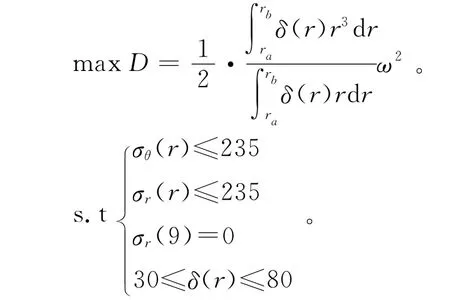
3 基于粒子群算法（PSO）的优化设计

3．1 算法设计

以D最大化为目标函数，在一个n维空间里，记粒子的当前位置为δ（r）i＝（δ（r）i1，δ（r）i2，…，δ（r）in），粒子的当前飞行速度为vi＝（vi1，vi2，…，vin），pi（pi1，pi2，…，pin）为粒子所经历过的最好位置，这里以目标函数为适应度函数，即粒子所经历过的最大目标函数的位置适应值最好［7］，则粒子i的当前最好位置pi（t＋1）为：

假如群体数为S，群体中所有粒子经历过的最好位置为pg（t），称为全局最优解，则：

D（pg（t））＝max｛D（p0（t）），D（p1（t）），…，D（ps（t））｝。速度与位置更新过程描述如下：

vij（t＋1）＝vij（t）＋c1rand（1）（pij（t）－δij（t））＋c2rand（2）（pgj（t）－δij（t））。

δij（t＋1）＝δij（t）＋vij（t＋1）。

其中：δij为第i个粒子在第j维的位置；pij为第i个粒子在n维空间里经历过的最好位置，即局部最优解；pgj为种群中粒子经历过的最好位置，即全局最优解；vij为粒子i的飞行速度；t表示第t代；rand（）为［0，1］范围内的随机数；c1和c2为加速度常数。

3．2 优化程序设计

在对飞轮结构所建模型以及PSO实现方法研究的基础上，运用MATLAB软件进行编程计算。程序模块包括应力计算模块、粒子群初始参数化模块、粒子位置与速度更新模块和寻优主模块。程序流程如图3所示。

本文中粒子群算法的初始化参数分别为：群体规模S＝200；加速度c1＝1．8，c2＝1．5。经过计算得到优化结果如下：图4为优化结果。

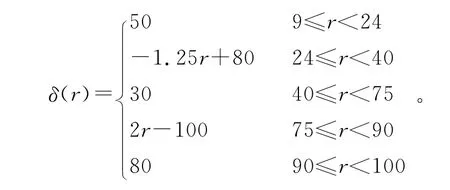
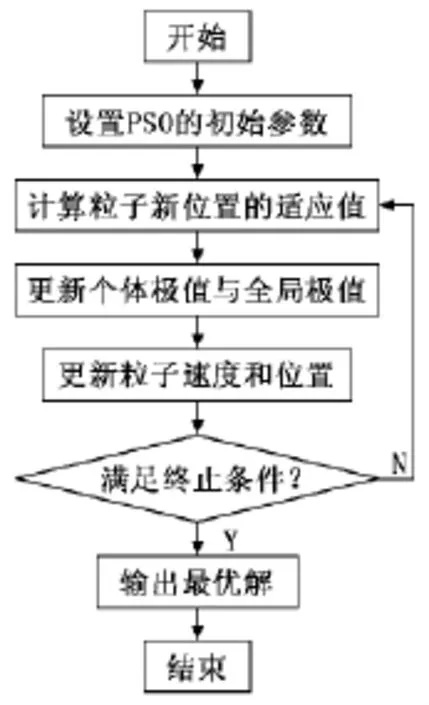
图3 程序流程图

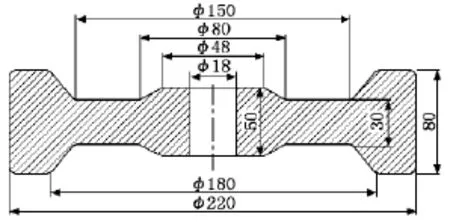
图4 优化结果图

4 优化飞轮的有限元分析

在给定设计转速15 000r／min下，运用ANSYS软件对上述计算得到的优化飞轮进行有限元静态分析和模态分析，得到相应的应力云图及结构模态，如图5～图7所示。

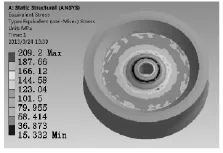
图5 应力分布

图6 应变分布

从图5可以看出，飞轮在设计转速下的最大应力为209．2MPa，小于普通碳钢的抗拉屈服强度235 MPa，有一定的安全裕量，满足强度要求，所以该优化飞轮的结构设计是合理的。通过计算得到优化飞轮（如图8所示）与等质量普通饼状飞轮（如图9所示）的储能参数，如表1所示。

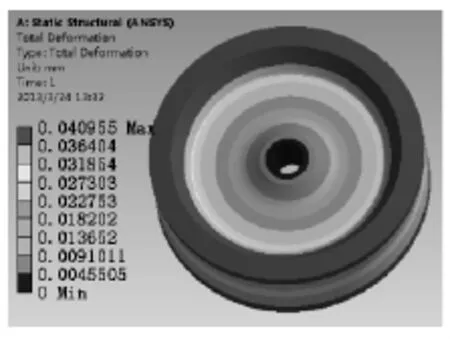
图7 总变形

图8 优化飞轮

图9 等厚饼状飞轮

表1 优化飞轮与饼状飞轮对比

优化结构后的飞轮储能密度为同等质量饼状飞轮储能密度的186．03%，优化后的飞轮储能性能大大提高。

5 结语

（1）本文基于粒子群算法和结构有限元分析软件ANSYS，在给定设计转速，同时满足结构强度、刚度、体积等约束条件的前提下，以飞轮储能密度最大化为目标，寻求磁悬浮飞轮的最优结构，优化结果令人满意。

（2）粒子群优化算法具有很好的全局优化能力，同时该算法的思路清晰，实现较容易，且该算法需要人为确定的参数较少，故优化结果比较客观、准确。

（3）本文所建立的参数化模型可用于储能飞轮系列产品的设计，能有效提高设计效率，缩短设计周期，降低制造成本。

［1］ 戴兴建，李奕良，于涵．高储能密度飞轮结构设计方法［J］．清华大学学报（自然科学版），2008，48（3）：378－381．

［2］ Arslan Ｍ Ａ．Flywheel geometry design for improved energy storage using finite element analysis［J］．Materials and Design，2008，29（2）：514－518．

［3］ Eby D，Averill R，Goodman E，et al．The optimization of flywheels using an injection island genetic algorithm［J］．Evolutionary Design by Computers，1999，13：167－190．

［4］ 郭振宇，叶敏，程博，等．基于差异演化算法的高速储能飞轮形状优化设计［J］．吉林大学学报（工学版），2008，38（1）：80－83．

［5］ 闫晓磊．储能飞轮优化设计理论与方法研究［D］．长沙：湖南大学，2011：15－17．

［6］ 徐秉业，刘信声．应用弹塑性力学［M］．北京：清华大学出版社，2003．

［7］ 茹忠亮，赵洪波，索玉萍．微粒群算法在结构优化设计中的应用［J］．河南理工大学学报，2006（10）：395－398．