考虑参数时变的电弧炉电极调节Terminal变结构控制

孙慧馨，黄志钢

(沈阳理工大学信息科学与工程学院，辽宁沈阳110159)

对电弧炉电极调节的研究国外起步较早，20世纪60年代，Billings等人［1］提出了电弧炉电极调节温度加权自适应控制算法，由于不能连续直接测试炉温，需要有可靠性较高的状态观测器，目前还无法满足这一要求。1990年美国Stanford大学的W.E.Staib等人［2］成功地将人工神经网络技术应用到电弧炉炼钢过程控制，开发出“智能电弧炉-IAF”。国内80年代，毛志忠等人［3］提出了电弧炉电极调节自校正控制方案与辨识方法;90年代后，北京科技大学张俊杰等人［4］在电弧炉的智能控制方面取得了一定的进展。

本文对电弧炉电极调节系统采用分段线性化方法得出系统模型，采用Terminal滑模变结构控制对系统进行快速跟踪控制，有效地抑制了抖振，通过仿真验证了这种方法的有效性。

1 电弧炉系统

电弧炉系统由电弧炉主电路及电极调节器组成，是一个复杂的非线性控制系统。具有以下特点:阶数高。使用比较简化的数学模型描述，系统的阶数也可达二十多阶;强非线性。交流电弧电阻具有很强的非线性;扰动复杂。大范围的扰动及随机性扰动并存，并且这种扰动存在于系统内部，是非加性的;强耦合性;调节过程的快速性。电极短路时，电极调节器必须及时将电极调至合适位置，这一过程通常为数秒［5］。

由于电弧炉电极调节过程是一个具有强烈非线性不稳定的控制过程，目前还没有一个准确的数学模型能够描述。本文根据文献［6］中采用的分段线性化的方法，将电弧炉电极调节系统进行分段线性化。

由于电弧电极调节过程是一个非线性过程，将电弧炉主电路看成是将电弧弧长映射为电弧电流随时间变化的非线性环节，即有

式中:I为电弧电流有效值;Lt为电弧弧长随时间变化量。对于持续性的弧长扰动，电弧炉电极调节系统可以简化为一个线性动态系统和一个非线性静态环节的串联系统，对于非线性静态环节进行线性化近似为N段，即

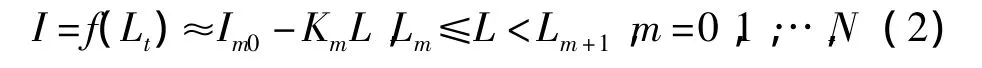
式中:Im0，Km＞0，随着分段的不同，弧长的大范围变化，Km的值也不同，是时变参数，Im0看作扰动。所以将电弧电极调节系统的第m个分段简化为图1模型。

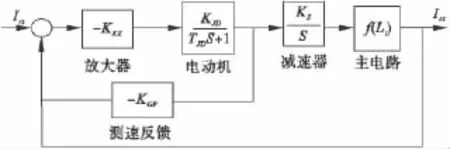
图1 电弧炉m分段系统结构框图

对于第m个时间分段区的系统，可以得到系统的传递函数为

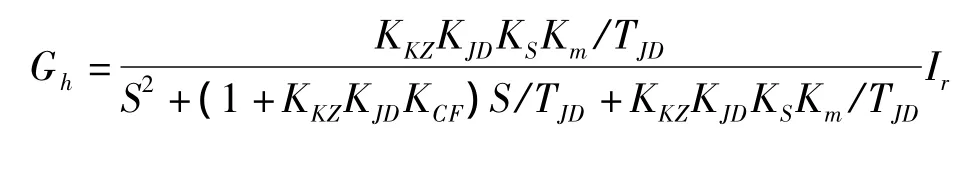
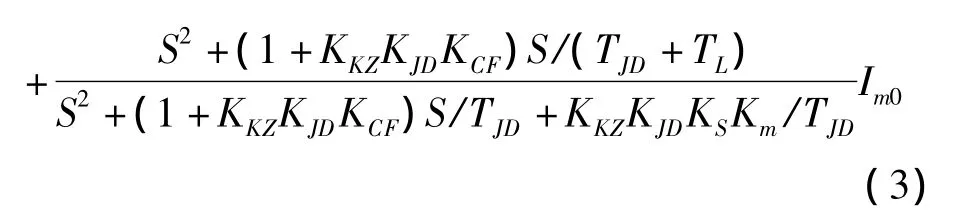
在分段m内，视扰动Im0=0，故系统传递函数简化为

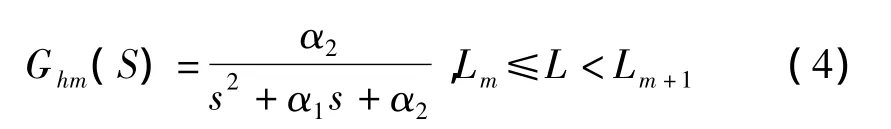
式中:α1=(1+KKZKJDKCF)/TJD为常数;α2=KKZKJDKSKm/TJD。在不同分段区，Km取值不同，随时间而变化;KKZ为晶闸管主电路的放大系数;TJD为交流电动机的机电时间常数;KJD为交流力矩电动机的放大系数;KS为机械传动装置的比例系数;KCF为测速发电机放大系数，其中忽略了电动机的电磁时间常数。

2 Terminal滑模控制器的设计

Terminal滑模控制是将滑模面设计为非线性函数与线性函数的结合，使得在滑模面上跟踪误差能够在有限时间内收敛到零，而且在系统偏离平衡点时又能快速回到平衡点位置，使得系统的动态性能优于普通滑模控制。并且相对于线性滑模控制，Terminal控制无切换项，可有效消除抖振，对系统不确定性和干扰具有很好的鲁棒性［7-8］。

Terminal滑动模态设计为［9］

式中:x∈R为状态变量;α;β＞0;p和q(p＞q)为正奇数。

在滑动模态上从任意初始状态x(0)≠0收敛到平衡状态x=0的时间为

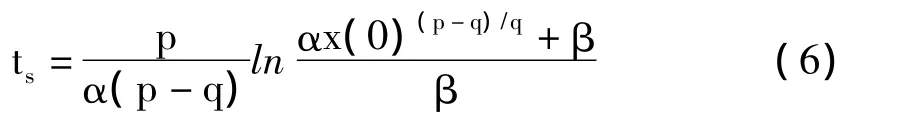
通过设定α，β，p，q可使系统在有限时间 ts内到达平衡状态。

滑模控制器的控制律设计为

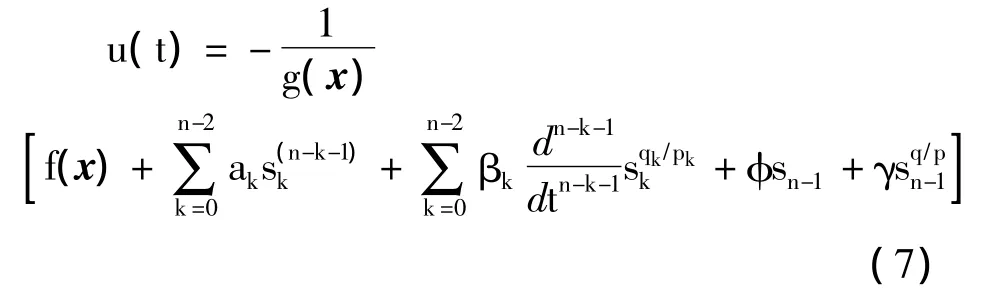
式中:s0=x1;g(x)，f(x)是Rn域中的光滑函数，g(x)≠0;φ，γ ＞0;k=0，1，…，n。

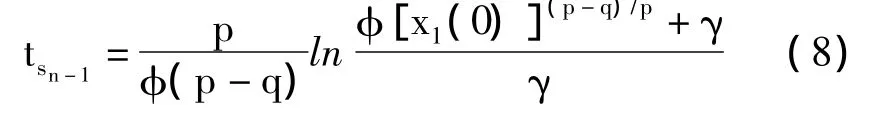
对于电弧炉电极调节系统，将传递函数写成微分形式

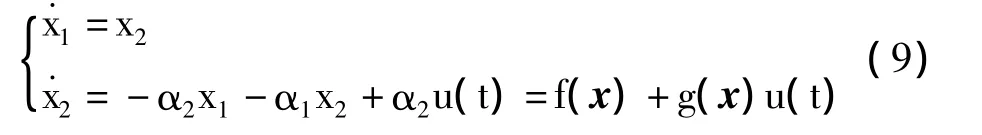
式中:g(x)为干扰源;u(t)为输入量。

通过查阅资料和参考某电弧炉厂的炼钢过程［6］，采集数据最后简化得出:

α1=15.554，α2=121，代入式(9)，对电弧炉进行Terminal变结构控制器的设计。

快速滑模面设计为

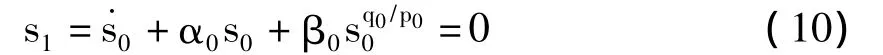
根据式(7)得全局快速滑动模态控制律为

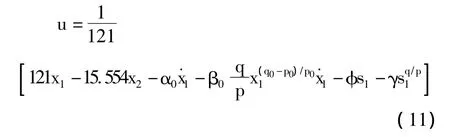
控制率参数取 α0=2，β0=1，p0=13，q0=7，φ =10，γ =10，p=3，q=1。根据式(8)得收敛时间为ts=1.83。

3 仿真验证

用Matlab进行仿真，通过仿真验证采用Terminal滑模变结构控制的电弧炉电极调节过程比传统PID控制效果好得多。图2为传统PID控制效果，图3为变结构控制效果。

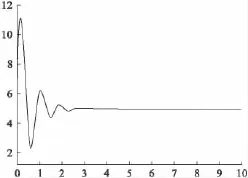
图2 PID控制效果图

从图2与图3可以看出，Terminal滑模变结构控制回到平衡点的速度明显比PID控制回到平衡点的速度更快，抖振很小，效果更好。

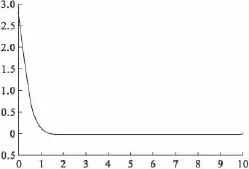
图3 Terminal滑模变结构控制效果图

4 结束语

通过仿真验证，采用Terminal滑模变结构控制的电弧炉电极能够较好地抑制抖振，具有较好的鲁棒性和快速性，比传统PID控制具有更好的效果，是以后发展的一个方向。对于电弧炉炼钢遇到的塌料问题和炼钢过程中复杂的干扰源没有解决，后续研究可以向模拟实物的变结构控制方向发展。

［1］Billing S.A，Boland P.M，Nicholson H.Electric and furnave modeling and control［J］.Automatiea，1979(4):137-148.

［2］William.E.Stuib.A Neuval Network Electrode Position Optimization System for the Electric An Furnace［J］.IJCNN，1992(6):10-14.

［3］毛志忠，李健.具有前馈环节的电弧炉电极开降自适应控制器［J］.东北大学学报(自然版)，1996，17(1):65-68.

［4］张俊杰，王顺晃.电弧炉炼钢过程终点自适应预报及专家指导系统［J］.自动化学报，1993，19(4):30-35.

［5］郭飞，李擎，李华德，等.交流电弧炉电极智能预测建模及应用［J］.电工技术学报，2007，22(12):175-179.

［6］刘小河，张道成.电弧炉电极调节系统的一种变结构控制［J］.自动化与仪器仪表，2003，107(3):22-25.

［7］刘金琨.滑模变结构控制MATLAB仿真［M］.北京:清华大学出版社，2005.

［8］王丰华.电弧炉建模研究及其应用［D］.上海:上海交通大学，2006.

［9］PAN YD，KRISHMA DK.Design of variable structure control system with nonlinear time-varying sliding zone［J］.IEEE Transaction On Automatic Control，2009，54(8):1981-1986.