薄壁铜管绕弯截面畸变的数值模拟及实验研究

王新鹏，刘劲松，，张士宏，张永靖，祝 炎

(1.沈阳理工大学材料科学与工程学院，辽宁沈阳110159;2.中国科学院金属研究所，辽宁沈阳110016;3.广东龙丰精密铜管有限公司，广东珠海519090)

薄壁管材弯曲零件在空调制冷、航空航天、汽车、船舶等行业中都有重要的应用，主要是薄壁管材弯曲零件能够满足产品轻量化、强韧化和低消耗等方面的要求［1-2］。铜管在材料和应用上的特殊性，其绕弯工艺与普通钢管弯曲工艺不同。就铜管而言，影响其弯管质量的因素主要有弯曲变形后管壁减薄和截面畸变(又称椭圆度)两个方面［3-4］。

目前，国内外许多学者对管材弯曲进行研究分析。Junichi Endow［5］采用能量法分析横截面畸变与材料性质及工艺参数之间的关系，理论与实验结果吻合得较好。Fode Paulsen［6］运用Marc有限元软件对矩形截面管材弯曲进行数值模拟，分析起皱、外侧塌陷、横截面畸变等缺陷，模拟结果与实际情况相符合。鄂大辛［7-8］在管材弯曲实验研究的基础上，对管壁厚变形和弯管横截面形状变形进行分析，认为壁厚变形主要受材料力学性能和变形几何因素的影响，短轴变化率可确切反映弯管扁平化的工程指标。Dino A.Oliveira［9］利用实验研究了不同种类润滑剂对不锈钢管数控弯曲成形的管件壁厚和表面质量的影响，获得特定条件下某种润滑剂的宏观响应，但摩擦对于绕弯成形的影响机理并没有涉及，特别是没有考虑摩擦对失稳起皱等缺陷的全面的影响机理。He Yang［10］采用实验与数值模拟相结合的方法研究摩擦对管材弯曲的起皱、壁厚减薄及横截面变形的影响，获得在小曲率半径弯曲中摩擦对壁厚减薄和横截面变形的影响要大于对起皱的影响，且弯曲半径越小这种作用越明显。申世军［11］建立理论解析模型推导计算包含芯棒直径、芯棒伸出量、芯头个数等参数的选取公式，并与实验结果吻合较好。Xu Jie［12］利用有限元模拟方法研究工艺参数对薄壁铝合金管的最大壁厚减薄率和最大截面畸变率的影响。结果表明管与防皱块间间隙为影响显著的参数，管与模具间间隙和摩擦、芯棒伸出量及助推速度为影响不显著的参数值。

本文采用有限元软件对薄壁铜管绕弯成形建立三维全过程模型，并以实验对模型计算结果进行了检验。结果表明，该模型能够准确有效地对绕弯成形过程进行模拟仿真。利用该模型分析芯棒直径、芯棒伸出量和摩擦系数工艺参数对横截面畸变的变化规律。

1 管材绕弯成形原理

铜管弯曲一般采用冷绕弯成形，绕弯成形以其高效率、高精确性的特点成为重要的管材弯曲成形工艺［9］，其成形原理如图1所示。由于铜管绕弯的相对弯曲半径通常小于1.5，所以弯曲成形时必须在管材内部插入芯棒起到支撑作用。弯曲装置主要有弯曲模、芯棒(芯杆和芯头两部分)、压力模、夹紧模等组成。铜管置于弯曲与夹紧模之间，并在其内部插入芯棒;夹紧模夹持铜管，使得铜管与弯曲模完全接触，然后夹持模与弯曲模以弯曲模中心为中心旋转设定的弯曲角度;夹紧模松开将弯管取出。

评价管材截面畸变率(椭圆度)ξ的公式为

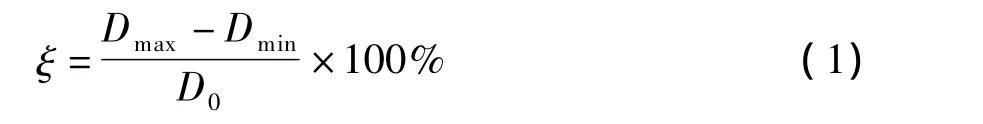
式中:Dmax为某截面最大直径;Dmin为某截面最小直径;D0为管材原始直径。

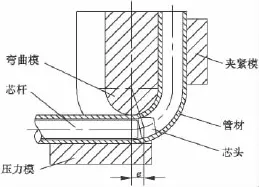
图1 管材绕弯工艺原理

2 有限元模型的建立

利用MSC.Marc/Mentat有限元软件对管材规格为Φ7.00mm×0.41mm，弯曲半径为10mm的TP2铜管弯曲成形进行模拟分析。几何模型共有夹紧模、弯曲模、管坯、芯棒、压力模5部分组成，如图2a所示。模型中模具均为面，并设为刚体。模型中管坯设为变形体，管材的相对壁厚较小，可以选取四节点壳单元，壳单元不仅能保证计算精度，且能提高计算效率，设定单元厚度为0.41mm，对主要变形区采取局部网格加密的方法提高计算准确性，划分单元数为6120。

物理模型的描述中包括变形体的材料特性、边界条件、接触条件、刚体与变形体的摩擦等。通过单向拉伸实验，获得TP2管材的常温力学性能，如表1所示。模型中管材与弯曲模、压力模、芯棒间接触界面采用通用接触;管材与夹紧模采用面-面接触。弯曲模、夹紧模设定只能绕Z轴转动，其余自由度固定，由给定速度控制;压力模、芯杆所有自由度均固定;芯头只给定绕Z轴转动的自由度，通过节点载荷控制。管材与模具之间均选用库仑摩擦模型，管材与夹紧模设为粘合关系，弯曲转动速度为1.57rad·s-1。

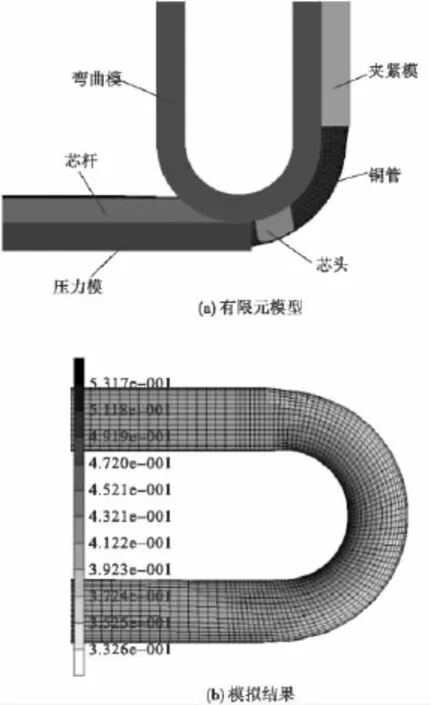
图2 有限元模型及模拟结果

表1 TP2管材的常温力学性能

3 实验验证

对 Φ7.00mm×0.41mm×10.00mm(外径 ×壁厚×弯曲半径)薄壁铜管，选用芯棒直径为5.96mm，调整芯棒伸出量为3.2mm，进行铜管弯曲实验研究。

利用数控弯管机将铜管试样弯曲，用线切割将试样沿横截面切开，用数显游标卡尺测量弯曲7个角度上的最大直径与最小直径，然后根据公式(1)计算出椭圆度并绘制曲线，如图3a所示;用千分尺测量7个角度管壁外侧厚度并绘制曲线，如图3b所示。经计算，椭圆度的实验测量值与模拟值之间的误差小于9%，外侧壁厚实验测量值与模拟值之间的误差小于5%。由此可得，该模型可以较好地对铜管绕弯成形进行模拟，其模拟结果与实际结果相符合。

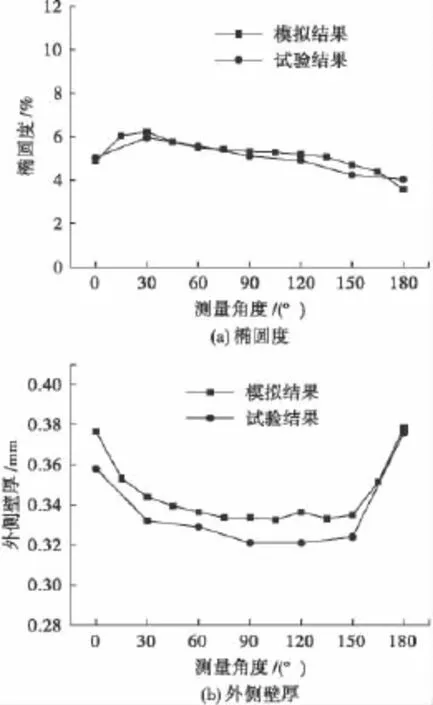
图3 实验值与模拟值对比

4 模拟结果分析

(1)芯棒直径对椭圆度的影响

芯棒直径的大小直接影响铜管在弯曲成形时横截面变形。在实际生产中，芯棒直径的选取通常参照经验公式D芯=(0.94～0.98)D内。图4为有限元模拟不同芯棒直径下铜管弯曲椭圆度的变化曲线。由图4可知，当芯棒直径为5.81mm(约为0.94D内)时，弯管变形区最大椭圆度为11.7%，已经超过允许值10%，芯棒直径大于5.93mm(约为0.96 D内)时，椭圆度的最大值均在8%以下，满足在中低压管的使用要求。因此，在铜管绕弯成形中按照经验公式的0.94 D内时不能满足正常生产需求，实际弯曲中其取值范围可确定为(0.96～0.98)D内。

(2)伸出量对椭圆度的影响

伸出量是指芯棒最大直径处提前弯曲中心的水平距离，通常用e表示，如图1所示。芯棒伸出量主要是指芯棒的安放位置，当芯棒伸出量过小时，使芯棒失去支撑作用造成椭圆度过大;当芯棒的伸出量过大时，在铜管弯曲变形时芯棒的芯杆部分会造成干涉。图5为有限元模拟不同伸出量下铜管弯曲椭圆度的变化曲线。从图5可以看出，但芯棒直径大于2.4mm时铜管的椭圆度小于8%，当伸出量为1.6mm时，在弯曲过程中芯棒不能很好地起到支撑作用，使管材的椭圆度迅速增加到11%。因此在调整模具时，应使芯棒伸出量e＞1/3D内，以控制铜管弯曲时横截面畸变量。

图4 芯棒直径对横截面的影响

图5 伸出量对横截面的影响

(3)摩擦对椭圆度的影响

摩擦主要是指管材与模具之间的摩擦，此处摩擦系数的改变是指改变管坯与弯曲模、压力模及芯棒之间的摩擦系数，夹紧模仍与管坯为粘合关系。图6为有限元模拟不同摩擦系数下铜管弯曲椭圆度的变化曲线。由图6a可以看出，当摩擦系数由0.1增大到0.3时，弯管的最大椭圆度由6.9%增大到8.6%。椭圆度随摩擦的增大而增加，但相对于芯棒直径和伸出量的变化而言，变化范围很小。管材与芯棒，管材与压力模之间的摩擦力随摩擦系数的增大而增大，摩擦力的方向与管材本身的拉力方向相同，则外侧变形区受到的拉力随摩擦系数增大而增大。外侧受到的拉力增加将使管材外侧壁厚的变化量增大，即外侧壁厚变得更薄，若过度减薄将出现外侧破裂。图6b为未使用润滑剂进行弯曲产生的铜管外侧破裂。

图6 不同摩擦系数铜管变形

5 结论

(1)利用有限元软件建立的有限元模型可以较好地对铜管绕弯成形进行模拟，壁厚计算值与实验值最大误差为5%，椭圆度计算值与实验值的最大误差为9%，模拟结果与实验结果符合很好。

(2)对于铜管绕弯成形而言，在相同弯曲半径、弯曲角度、伸出量和润滑相同的条件下，椭圆度随芯棒直径的增大而减小，当芯棒直径大于5.93mm(约为0.96 D内)时椭圆度小于8%。

(3)在相同弯曲半径、弯曲角度、芯棒直径和润滑相同的条件进行弯管时，椭圆度随芯棒伸出量的增大而减小，当芯棒伸出量e＞1/3D内能够控制椭圆度在8%以下。

(4)铜管绕弯成形中，椭圆度随摩擦系数的增大而增大，在润滑不充分时容易产生弯管外侧破裂。

［1］F.Stachowicz.Bending with upsetting of copper tube elbows［J］.Journal of materials processing technology，2000(100):236-240.

［2］刘劲松，张兴华，刘海，等.薄壁钢管内胀推弯成形数值模拟及实验研究［J］.锻压技术，2012，37(2):63-67.

［3］王同海.管材塑性加工技术［M］.北京:机械工业出版社，1998.

［4］寇永乐，杨合，詹梅，等.薄壁管数控弯曲截面畸变的实验研究［J］.塑性工程学报，2007，14(5):26-31.

［5］Junichi Endow，Tadao Murota.On the flattening of cross-Section of circular tubes in uniform bending［J］.Advanced technology of plasticity，1984，32(1):285-290.

［6］Fode Paulsen，Torgeir Welo.Application of numerical simulation in the bending of aluminum-alloy profiles［J］.Journal of materials processing technology，1996(58):274-285.

［7］鄂大辛，宁汝新，唐承统，等.小直径管无芯弯曲壁厚变形的试验研究［J］.塑性工程学报，2004，12(2):56-61.

［8］鄂大辛，王险峰.弯管扁平化的平面应力分析及相对弯曲半径［J］.塑性工程学报，2007，14(4):25-28.

［9］Dino A.Oliveira，Michael J.Worswick，Rassin Grantab.Effect of lubricant in mandrel-rotary draw tube bending of steel and aluminum［J］.Canadian metallurgical quarterly，2005，44(5):71-78.

［10］He Yang，Heng Li，Mei Zhan.Friction role in bending behaviors of thin-walled tube in rotary-draw-bending under small bending radii［J］.Journal of materials processing technology，2010(210):2273-2284.

［11］申世军，杨合，李恒，等.薄壁管小半径数控绕弯成形芯模效应的实验研究［J］.塑性工程学报，2007，14(4):29-34.

［12］Jie Xu，He Yang，Heng Li.Significance-based optimization of processing parameters for thin-walled aluminum alloy tube NC bending with small bending radius［J］.Transaction of nonferrous metals Society of China，2012，22(1):147-156.