基于屈服体积比的拱坝整体稳定尖点突变模型

李季琼 ， 宋鹏 ， 王少伟 ， 刘 颖

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏 南京 210098；3.河海大学水利水电学院，江苏 南京 210098；4.扬州市勘测设计研究院有限公司，江苏 扬州 225007）

拱坝由于其力学性能优良和工程造价经济的特点，已成为我国水电建设中的主要坝型之一。我国目前已建或在建的坝高超过100 m的拱坝有20多座， 如锦屏一级 （305 m）、 小湾 （294.5 m）、 溪洛渡 （285.5 m）等。这些工程大多位于西部地区，地形地质复杂、地震灾害频繁且地震烈度高，拱坝安全面临严重威胁，给国民经济和人民生命安全带来隐患。因此，研究拱坝整体稳定分析方法，确定拱坝整体安全度对掌握工程安全状况有重要意义。

根据现代力学的稳定性理论[3]，拱坝整体失稳破坏时系统由静止状态向可动状态转变，其中衡量拱坝整体稳定的指标是拱坝整体安全度。目前，研究拱坝整体安全度的主要方法有超载法、强度储备法和综合法等，拱坝是否达到失稳临界状态的判据包括收敛性判据和突变性判据[2]，前者以迭代计算过程不收敛作为失稳判据，后者根据 “位移-荷载”或“位移-强度”关系曲线的突变点，结合塑性区贯通情况进行判断，但是，采用哪个节点或哪个方向的位移目前还没有统一的认识，位移突变点和塑性区贯通指标的确定也缺乏量化标准，分析存在诸多不确定性。因此，笔者基于突变理论，将拱坝坝体的屈服体积比这一单值标量作为失稳考察量，建立拱坝整体稳定分析的尖点突变模型，用以确定拱坝整体安全度，实现失稳判据的量化。

1 尖点突变理论

突变理论是以分叉理论、奇异理论和拓扑学为数学工具，用以分析如岩石突然断裂、桥梁突然坍塌、拱坝失稳等传统的微积分方法不能解释的不连续变化现象的数学分支[4]。拱坝一般在容许荷载作用下变位光滑连续，但是，当坝体或基岩刚度不足，拱坝或岩基会突然失稳，由一种连续状态跳跃到不连续的状态，该失稳突变过程具有多模型态、不可达性、突跳性、滞后性、发散性等特征[1]，可采用尖点突变模型予以判别，其几何形状如图1所示。

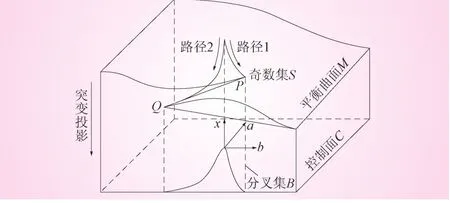
图1 尖点突变模型

尖点突变模型的标准势函数[5]为

式中，x为状态变量；u、v为控制变量。

该势函数对应三维状态空间，当势函数有唯一的极值时，系统处于稳定状态；当系统处于失稳状态时，势函数有多个极值。临界点方程可由势函数求一阶导数得到

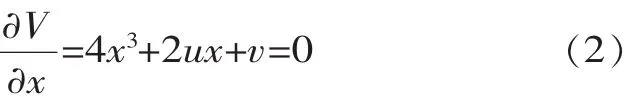
式（2）同时给出系统的平衡曲面，该曲面上、下叶对应稳定的平衡位置；对应于曲面中叶的平衡位置是不稳定的。对于u、v的任意变化，空间相点在平衡变化到达上叶或下叶的边缘时会发生突变而越过中叶，在平衡曲面上将满足：

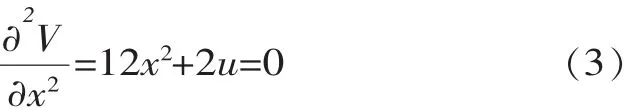
由式（2）、（3）联立求解，消去x可以得到势函数的分叉集：

当Δ>0时，系统处于稳定状态；当Δ=0时，系统处于临界失稳状态；当Δ<0时，系统处于非稳定状态。式（4）即为系统整体稳定与否的判据。

2 拱坝整体稳定的尖点突变模型

采用强度折减法分析拱坝系统 （包括坝体和坝基）的整体稳定安全，随着材料强度逐步降低，拱坝屈服破坏区域逐渐扩展，坝体的屈服体积比将不断增大，直至结构丧失承载能力而发生整体失稳破坏。因此，拱坝失稳过程将伴随坝体屈服体积比逐渐增大直至突变，可以将坝体屈服体积比作为失稳考察量，建立尖点突变模型评价拱坝整体稳定性。采用强度折减法进行非线性有限元分析，得到多级强度条件下的坝体屈服体积比，从而获得屈服体积比与强度折减系数的对应关系。一般可以认为坝体屈服体积比是强度折减系数的连续函数，根据尖点突变理论，建立坝体屈服体积比Q与强度折减系数k的尖点突变模型势函数

由于尖点突变模型的标准势函数为四次多项式，考虑精度要求，取四次多项式进行拟合

式中， ai（i=0～4）为多项式系数。

采用Tschirnhaus变化，对式（6）作系数变换，转化为尖点突变模型的标准形式。为此，引入状态变量Y和中间变量L，令k=Y－L，可以得到

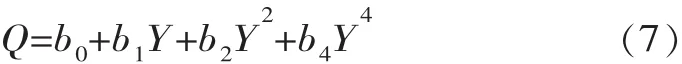
其中，

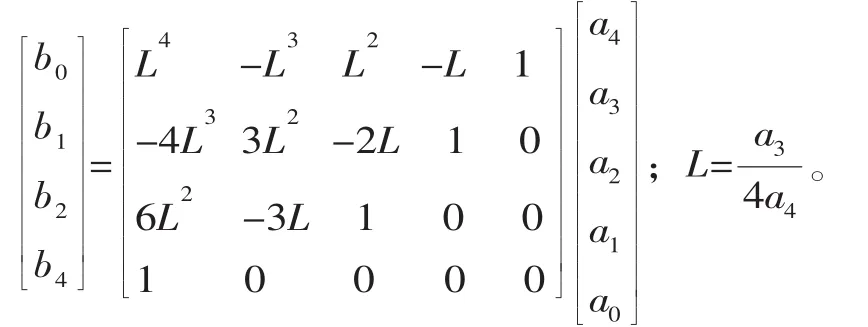
在式（7）中， 令

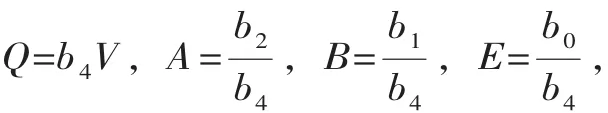
则得到尖点突变模型的标准势函数为

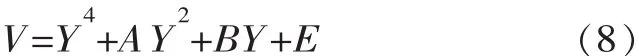
删除式（8）中的常数项E不改变V的性质，这样可以得到形如式（1）的势函数。因此根据尖点突变理论，拱坝系统整体稳定状态的判别式为

当Δ>0时，拱坝系统处于稳定状态；当Δ=0时，拱坝系统处于临界失稳状态；当Δ<0时，拱坝系统处于非稳定状态。

3 工程实例

3.1 有限元计算模型

某碾压混凝土拱坝坝顶高程1 274.5 m，最大坝高94.5 m，坝顶长252.3 m，宽6.0 m，坝底宽20.0 m。根据地质资料，以拱冠梁剖面为参考，向上游取1倍坝高，向下游取2倍坝高，沿顶拱坝肩向左、右岸各取1倍坝高，建基面以下取1倍坝高，建立三维有限元模型。有限元网格主要采用八节点六面体单元，局部区域以六节点五面体单元过渡，共划分7 585个单元和8 228个节点，其中坝体单元2 860个，节点3 835个。模型底面为三向固定约束，上下游边界和两岸边界分别施加法向约束。计算工况为正常蓄水位的基本作用组合，荷载包括坝体自重、水压力 （正常蓄水位1 272.0 m）、温降、淤沙压力和扬压力。采用强度折减法进行非线性有限元分析时，坝体和基岩各部位的材料均采用基于线性Mohr-Coulomb屈服准则的弹塑性本构模型。拱坝系统各部位材料的主要力学参数见表1。混凝土的热膨胀系数为8.5×10-6/℃。

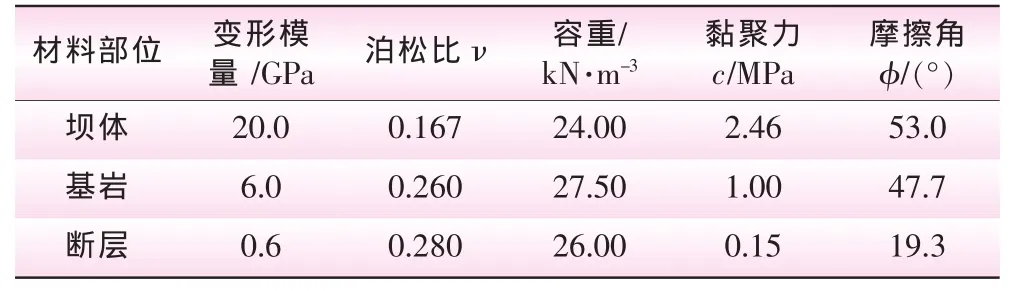
表1 拱坝系统不同部位材料的物理力学参数

3.2 成果分析

3.2.1 基于屈服体积比的拱坝整体安全度评判

在强度折减法计算过程中，等比例降低坝体和基岩的材料抗剪强度，强度折减系数从1开始，以0.1为间隔，逐级递增。采用经过折减的材料强度参数对拱坝系统进行有限元计算，得到各级强度条件下的坝体屈服体积比。根据屈服体积比与强度折减系数关系曲线 （如图2a所示）的变化特征初步判断拱坝系统的整体安全度在1.70~1.90之间。因此，从k=1.70开始，以0.01为间隔，再次逐级降低材料抗剪强度进行计算，得到屈服体积比与强度折减系数的关系曲线如图2b所示。

当强度折减系数为ki从1.70开始时，对前i个k与相应的坝体屈服体积比Qi进行四次多项式拟合，通过式（6）~（9）可求得不同折减系数ki对应的突变特征值Δi。 Δi将随着ki增大而逐渐减小， 当Δi=0时， 认为拱坝系统处于稳定临界状态，此时的ki即为强度储备安全度。

当折减系数k取1.81时， 对ki（i=1~12）和相应的坝体屈服体积比Qi（i=1~12）进行四次多项式拟合，得到

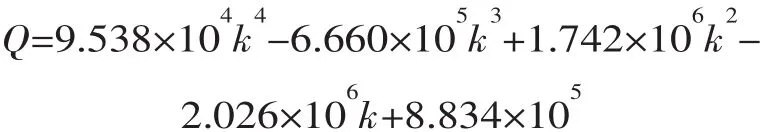
由式（8）通过系数变换，建立尖点突变模型的标准势函数为

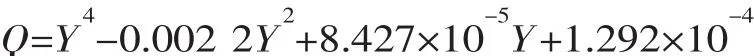
根据式（9）可以得到坝体屈服体积比的突变特征值为

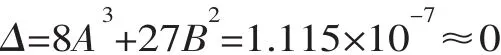
据此可以认为拱坝系统处于稳定临界状态，整体强度储备安全度为1.81。图3、4分别为k=1.40和k=1.81时坝体及坝基屈服区的分布情况。k=1.40时，坝体中低高程上游坝面两侧拱端受拉屈服，下游坝面两侧拱端受压屈服；建基面中低高程坝踵和坝趾部位出现屈服区。随着坝体和基岩材料强度降低，上、下游坝面的屈服区向上部延伸，并沿坝厚方向向坝体内部扩展；建基面坝踵、坝趾部位的屈服区逐渐扩大，在中低高程开始局部贯通，并沿岸坡向上部延伸。k=1.81时，左右坝肩中下部已全部屈服贯通，建基面中低高程的坝肩岩体全部屈服贯通，根据塑性屈服区贯通判据，拱坝系统已处于失稳状态。因此，该拱坝系统的整体强度储备安全度为1.81。

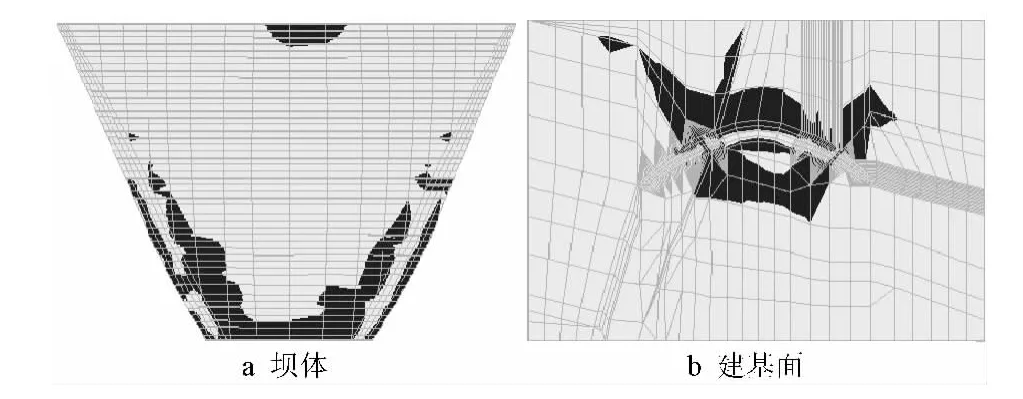
图3 k=1.40时坝体和建基面塑性屈服区分布

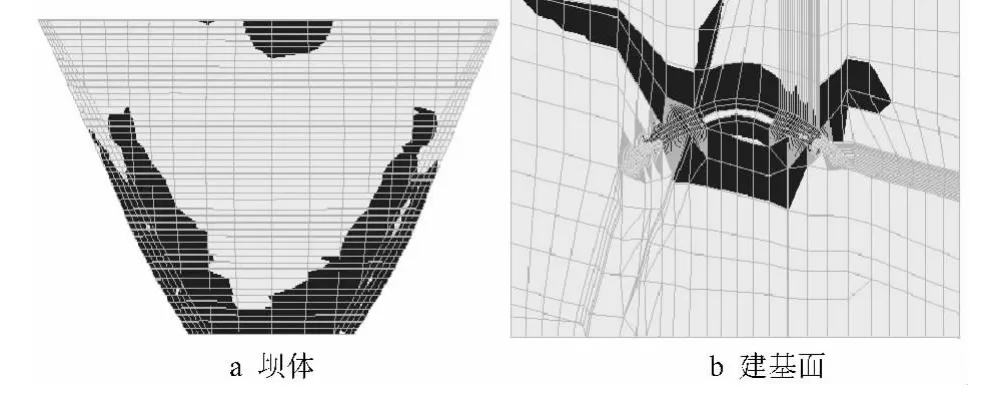
图4 k=1.81时坝体和建基面塑性屈服区分布

3.2.2 拱坝整体稳定的位移突变分析

位移突变法根据计算域内某一部位位移与强度折减系数关系曲线的变化特征确定拱坝整体安全度。该方法物理意义明确，但是对于位移考察点的选择目前还没有统一认识。笔者选取拱坝拱冠梁坝顶顺河向位移、左岸1/4拱圈坝顶顺河向位移、右岸1/4拱圈坝顶顺河向位移作为考察量，根据上述位移与强度折减系数关系曲线的突变点评价拱坝整体安全度，得到如图5为所示关系曲线。从图中可以看出：右岸1/4拱圈坝顶顺河向位移在k=1.80时产生突变，左岸1/4拱圈坝顶和拱冠梁坝顶顺河向位移均在k=1.81时产生突变。据此可以判断拱坝整体强度储备安全度为1.80，且位移的突变是从右岸坝体开始的，然后逐渐扩展至左岸坝体，位移考察点的选取对拱坝整体安全度的计算结果有较大影响。

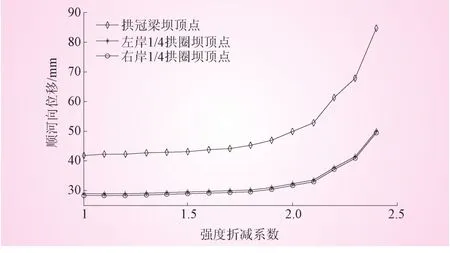
图5 坝体顺河向位移与强度折减系数关系曲线

综上所述，采用基于屈服体积比的尖点突变模型和位移突变法研究某拱坝系统的稳定安全，得到拱坝的整体强度储备安全度分别为1.81和1.80。结果表明：两种方法评价结果基本一致，以屈服体积比作为失稳考察量，物理意义明确，评判结果唯一；采用位移突变法研究拱坝整体安全度，位移考察点的选取对计算结果影响较大，位移突变点往往依据经验确定，受人为主观因素影响较大；基于屈服体积比的尖点突变模型可以实现拱坝整体失稳的量化判定。

4 结语

采用强度折减法对拱坝系统进行非线性有限元计算，以坝体屈服体积比作为拱坝整体稳定状态的考察对象，建立了拱坝整体稳定尖点突变模型。将拱坝整体稳定性判别归结为突变特征值 的正负问题，有效避免了已有评价方法中人为因素的影响，实现了系统稳定性态的量化判定，且评判结果与已有的定性评价方法一致。另外，拱坝的坝体屈服体积比为单值标量，以其作为失稳判据，受局部材料强度和结构特征的影响较小，可以避免塑性贯通判据尚无客观指标和位移突变判据中失稳控制点选择的问题，结果唯一，便于分析和应用。

［1］顾冲时，吴中如，徐志英.用突变理论分析大坝及岩基稳定性的探讨［J］.水利学报， 1998（9）:48-51.

［2］任青文.高拱坝安全性研究现状及存在问题分析［J］.岩土力学,2007， 38（9）:1023-1031.

［3］任青文.灾变条件下高拱坝整体失效分析的理论与方法［J］.工程力学， 2011， 28（S2）:85-96.

［4］ARNOLD V I.Catastrophe theory［M］.北京： 高等教育出版社，1990.

［5］凌复华.突变理论及其应用［M］.上海：上海交通大学出版社,1987.

［6］宋鹏，程琳，田振华，等.高拱坝安全度计算方法对比分析［J］.水力发电， 2012， 38（10）:36-39.

［7］郑东健，雷霆.基于突变理论的高拱坝失稳判据研究［J］.岩土工程学报， 2011， 33（1）:23-27.

［8］王少伟，夏辉，崔英杰，等.基于突变理论的拱坝整体安全度分析［J］.河海大学学报 （自然科学版）， 2012， 40（5）:543-548.

［9］顾冲时，吴中如.大坝及坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006.

［10］任青文，钱向东，赵引，等.高拱坝沿建基面的破坏和安全度研究［J］.水力发电， 2002（12）:10-13.