城市火灾次数与气象因子的分位数回归分析

刘盼盼， 周嘉章， 谭常春

（1.合肥工业大学 数学学院，安徽 合肥 230009；2.安徽省气象局 培训中心，安徽 合肥 230031）

随着经济科技的不断发展，火灾发生频率也日趋上升，导致火灾发生的相关因素非常复杂，有社会因素、环境因素及气象因素等，但不管是何种原因引发的火灾，都不可避免地给人们带来精神和物质上的双重伤害，而国家和政府也要投入大量的人力、物力和财力去弥补火灾造成的损失。所以，研究火灾的发生规律迫在眉睫。

从气象因素分析火灾的发生规律一直是研究热点，其中，关于森林火灾的研究较多，文献［1］建立林火与气象因素的广义线性模型，揭示各气象因素与林火发生的概率关系；文献［2］运用多元回归分析理论建立气象因子的火灾面积预测模型，较好地预测林火发生后林地可能的过火面积。

近年来，我国对城市火灾数据的研究也日益增多，特别是在火灾发生与气象因素相关性的研究方面，取得了一定的成果。

文献［3］从某市火灾数据出发，采取逐步回归和着火危险度分析法研究火灾发生次数与气象因素间的关系。

文献［4］利用北京市1997—2000年间的火灾数据，通过季节调整消除季节效应带来的影响，又把各气象因子滞后期对火灾次数的影响考虑在内，建立了火灾次数与各气象因素的自回归模型。

文献［5］采用多元线性回归的思想，通过逐步回归法剔除与火灾次数相关性较弱的气象因子，逐步得到火灾次数与气象因子的回归模型，并利用此模型对2008年火灾形势做了预测。

文献［6］通过因子分析和线性回归法建立了关于火灾次数与气象因素之间不同的回归模型，经过分析比较，得到最优模型。

以往的线性回归模型只关注因变量的条件均值，而没有考虑因变量的完整特征，对于非中心位置的解释不明确，特别是对着重关注尾部特征的主题（工资、收入、财富），采用条件均值框架分析忽略了其他更重要的分布特征［7］。

为了弥补这一不足，文献［8］提出了分位数回归的方法，该方法在最近几年不断发展，其应用范围也越来越广泛，应用领域涉及经济［9－11］、医学［12－13］及环境科学［14］等各个方面。

本文将分位数回归法应用到火灾次数与气象因素的相关性研究上，因为分位数回归能够解释不同时期的火灾发生次数与气象因素之间的关系，符合人们着重关注火灾高发期这一尾部特征的需求。

1 分位数回归的方法

传统的回归分析采用因变量条件均值函数描述自变量每一特定数值下的因变量的均值，从而揭示自变量与因变量的关系。然而，分位数回归则主要是通过被解释变量Y的条件分位数对解释变量X 进行回归，即

类似于传统线性回归模型，分位数回归模型可表示为：

与传统线性回归的主要区别在于模型中参数估计方法不同，传统线性回归是利用最小二乘法求参数估计，即而分位数回归中参数估计则通过给定因变量Y的分位数τ，然后利用加权残差最小求参数估计，具体为：

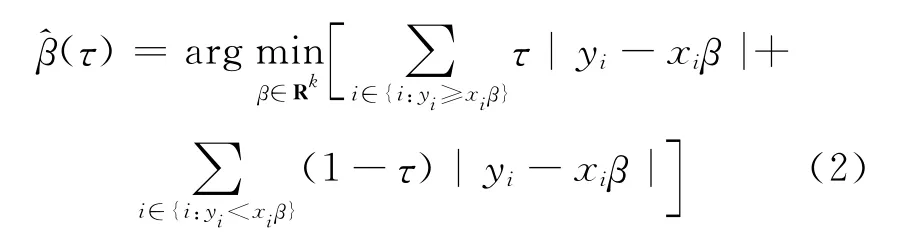
（2）式可等价为：

其中，ρτ（μ）＝μ（τ－I（μ））是损失函数，I（μ）为示性函数，即

分位数回归有很多优点，它避免了随机扰动项分布的假定，一定程度上克服了异方差的问题；可以在不同分位数水平上进行回归，能很好地减小异常值带来的影响，使模型具有很强的稳健性；分位数回归的参数估计在大样本下具有很好的渐近优良性。

2 实证分析

2.1 数据说明与分析

本文采用某市1997—2007年间的火灾数据，其中，1997—2003年的火灾数据来自文献［15］，2004—2006年的火灾数据来自文献［16］。

选择这10年的数据是因为1997年实施了新的火灾统计方法，新方法的实施影响了火灾数据的连续性，使1997年前后的火灾数据失去可比性。而到了2007年，火灾统计标准也发生了改变，火灾次数由消防队出火警次数变为造成损失的火警次数，为保持与以往数据的连贯性，本文选择由该市消防局记录的月火警次数作为2007年的火灾次数。

由分位数的定义并利用R软件求得火灾次数（记为F）的0.25和0.75分位数分别为287.5和562.25（记为和）。如果月火灾次数大于，就称其为火灾高发期，若月火灾次数小于，则称此月为火灾低发期。本文对该市11年间的月火灾次数做了相关汇总，结果如图1所示。从图1中可以看出，火灾高发期主要集中在1、2月份，该市冬季天气寒冷，干燥少雪，受季风的影响很大，又加上春节期间烟花炮竹燃放点增多，家用取暖设备的使用量上升，这些因素都不可避免导致火灾的发生。

图1 不同月火灾次数下月份个数图

由图1可知，8月份火灾发生次数最少，因为该市7—9月的降水量高达全年降水量的75%，加之夏季高温，湿度大，导致夏季和初秋时节火灾不频繁。

2.2 数据处理

在建模之前，对上述数据中火灾次数与各气象因素进行了相关性分析，火灾次数与温度、湿度、风速及降水量各气象因素相关系数很小，分别为－0.448 5、－0.373 5、0.081 8和－0.387 5。为了增强它们之间的相关性，需对原始数据做相应的变换，一般采用对数变换。

由于原始数据中有负值，会影响数据做对数变换，所以首先把温度都转化为绝对温度，湿度、风速、降水量的值都加1，火灾起数F不变，这样保证了所有数据都为正值。

然后对所有数据取自然对数，得到月平均对数绝对温度ln T、月平均对数相对湿度ln H、月平均对数风速ln W、月平均对数降水量ln R及火灾对数次数ln F；最后利用对数变换后的数据做回归分析。

2.3 线性回归与分位数回归结果分析

利用上述变换后的数据建立分位数回归模型，即

2017年8月25日，《南方周末》发布《南方周末反侵权声明》。文章指出，随着移动互联网的日渐繁盛，大量媒体、网站、移动客户端、自媒体平台等违反相关法律法规，未经授权擅自转载南方周末报纸、官网以及旗下其他官方自媒体平台刊发的作品，要求尊重原创。截至2017年8月15日，已处理非法转载文章3013篇，对和讯网、投资界等14个网站提起诉讼。2017年7月，在起诉国内两家知名门户网站非法侵权转载南方周末文章的案件中均获胜诉。

选择5个具有代表性的分位点，分别为0.10、0.25、0.50、0.75、0.90，利用 R 软件做回归，回归结果见表1所列。

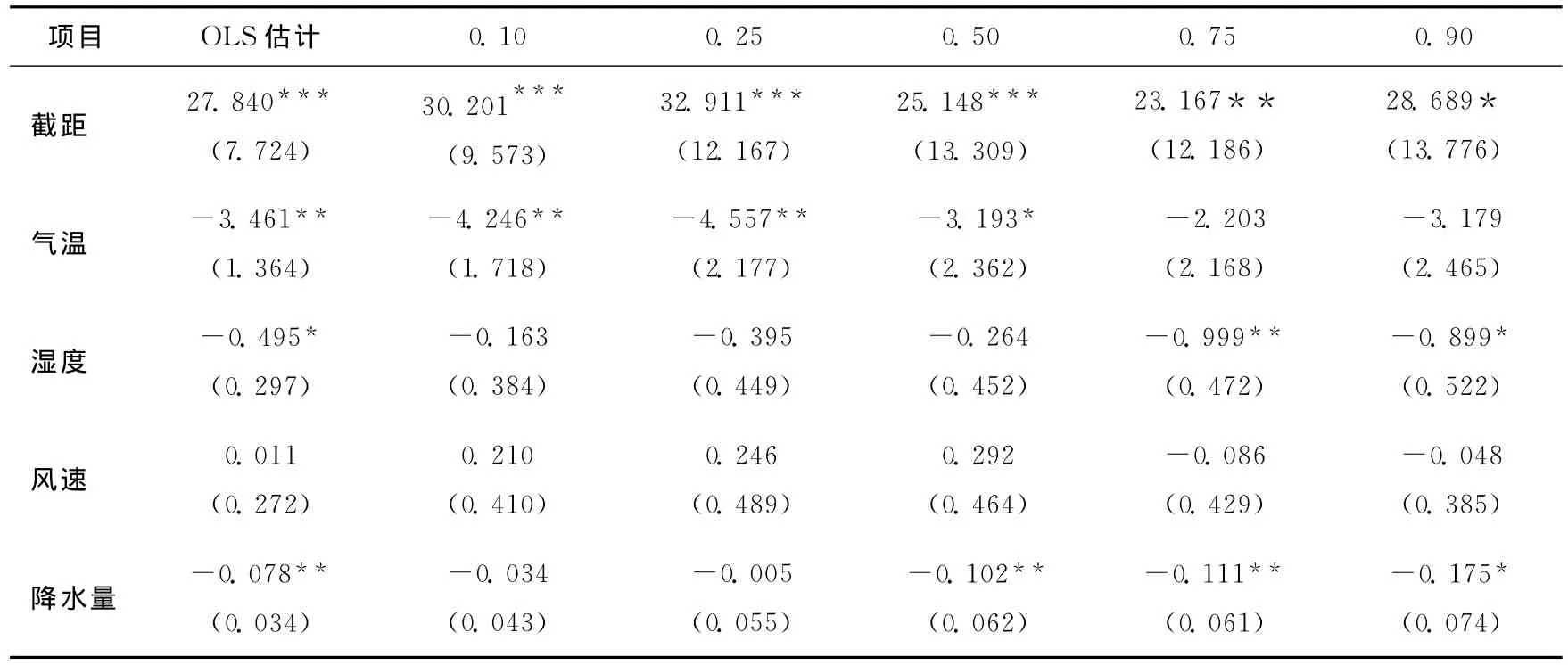
表1 各分位数回归结果

比较表1各列结果，可得如下结论：

（1）由第1列OLS结果可知，温度、湿度、降水量这3个因素的系数估计值都通过了相应的显著性检验，说明这3个因素对火灾次数的影响是显著的。又由各估计值为负得知火灾次数与气温、湿度、降水量呈负相关，并且从各参数的估计值大小看，气温因子对火灾起数的影响最敏感，因为在其他条件不变的情况下，对数绝对温度每上升1个单位，火灾对数次数就会减少3～4起。

（2）在0.10、0.25、0.50、0.75、0.90这5个分位点上的回归结果显示，低分位处只有温度对火灾次数影响显著，中位数处温度和降水对火灾次数影响较大，而高分位处对火灾次数影响显著的是湿度和降水量，说明在不同季节火灾次数与各气象因素的关联程度是不同的。

2.4 分位数回归结果图形报告与分析

为了更加直接地看出同一因子在不同分位点上对火灾次数影响的差异，本文做出了对应的系数估计值图形，报告了不同分位数下的参数估计值及其相应的90%置信区间，如图2所示。

图2 分位数函数图

其中，灰色区域表示90%置信域，2条实线中一条是0线，另一条是OLS估计值，2条虚线分别表示OLS估计的上、下限。

图2a中截距表示在自变量均值上的拟合分位数函数，可认为是各气象因子值为0时，火灾次数随分位数的变化图。从图2a不难看出各分位点处的截距都远远高于0线，说明火灾次数除了受气象因素的影响外，还受其他因素的影响。

表1中10%、25%的火灾低发期和火灾高发期温度的回归系数分别为－4.246、－4.557和－3.193、－2.203，在其他条件不变的条件下，由回归系数为负可知，在火灾高发期和火灾低发期，对数绝对温度的升高均可以减少火灾次数，即高温天气不易发生火灾。除此之外，图2b中中位数以下的置信封闭区间并没有穿过0线，而中位数以上置信封闭区间穿过了0线，表明在夏季温度对火灾次数的影响大于冬季。因为夏季空气湿度大，降水量多，在保持这些气象因子不变的情况下，升高温度会加快水分蒸发，直接影响易燃物品的含水量，抑制火灾发生。而冬季干燥少雨少雪，升高温度并不能有效改变空气湿度，所以冬季温度对火灾发生的影响不显著。

结合表1和图2c可知，湿度与火灾次数成负相关，湿度越大，可燃物含水量越大，就越不容易达到着火点，火灾发生的机率就越小。夏季高温多雨，温度高使降水蒸发快，空气湿度大，可燃物水分含量大，此种条件下增大湿度以减少火灾的发生，其意义不大，所以湿度系数估计值在火灾低分位点没能通过相应的显著性检验。冬季温度、降水量与夏季相反，干燥缺水，此时增大空气湿度就能较好地抑制可燃物点燃，从而抑制火灾的发生。

不管是OLS估计还是分位数回归估计，风速因子的参数估计均未通过显著性检验，这一信息在图2d中展现得非常清楚，因为整个置信封闭区间都穿过0线。但是这一因子对火灾次数的影响在不同分位点处是有差异的。在0.10、0.25低分位点和0.50中分位点处，风速与火灾次数呈正相关，加大风速可以使火灾蔓延，导致第2火场，增加火灾次数。在0.75和0.90高分位点处，风速与火灾次数呈微弱负相关。因为冬季温度低，可燃物遇雨雪容易结冰，即使有寒风也很难发生飞火，从而避免第2火场出现；冬季寒风风速较大，有吹灭小型火灾的可能性。

降水量因子的系数估计值在0.10和0.25低分位点处趋于0，表明夏天增加降水量对减少火灾次数的作用不明显，因为夏季降水量充沛，导致火灾发生的主要因素不在于缺乏降水。而在0.50中位数和0.75、0.90高分位处情况截然不同，降水量对火灾影响的显著性明显增强，冬季增加降水，雨水结冰不易流失，易燃物在地面不易着火，火灾次数会相对减少。

从上述对OLS估计与分位数回归估计进行的分析比较，不难发现，从分位数回归估计不仅能看出OLS估计反映出的火灾次数与气象因素的正负相关性，而且它能更加细致地反映出在什么时候、哪种气象因素对火灾次数的影响显著，从而为不同季节预防火灾的发生提供了理论依据。

2.5 预测

分位数回归是因变量的条件分位数对自变量的估计，所以对特定的分位点τ而得到的回归模型，应该对因变量τ分位点附近的预测效果好。为了验证预测效果，对上述所有2月份的火灾次数做预测，因为2月份是火灾高发月，所以选取τ为0.8时的分位数回归模型进行预测，预测结果如图3所示。其中曲线1表示τ为0.8时分位数回归模型预测结果，曲线2表示原始数据，曲线3表示OLS估计的预测结果。

图3 对数火灾次数预测图

图3中OLS估计预测结果几乎都在原始数据以下，而且分位数回归预测出火灾次数趋势更接近原始数据，误差较小，所以分位数回归更能解释火灾高发期火灾次数与气象因子的相关性。

3 结束语

本文研究4个气象因子对火灾起数的影响，主要运用分位数回归的方法建立回归模型。从回归结果可见，它不仅反映出OLS估计信息，更细致地展现出在不同分位点上各因子对火灾起数的影响不同，而且同一个因子在不同分位点上对火灾起数的影响也不同。

［1］田应福，金百锁，缪柏其，等.日本林火的广义线性模型［J］.统计与决策，2006（7）：50－52.

［2］曲智林，胡海清.基于气象因子的森林火灾面积预测模型［J］.应用生态学报，2007，18（12）：2705－2709.

［3］崔 锷，许学雷，孙立勇.城市火灾与气象因素的相关性分析研究［J］.火灾科学，1995，4（2）：61－64.

［4］黄 韬，柳国忠.城市火灾起数与气象因素的自回归模型研究［J］.中国安全生产科学技术，2008，4（3）：164－166.

［5］刘 宁，祝国苓.火灾与气象因素的相关性研究［J］.武警学院学报，2010，26（2）：22－25.

［6］谭常春，周 尧.城市火灾次数与气象因素的回归模型［J］.统计与决策，2011（18）：31－33.

［7］张 涛.工资收入差异：基于分位数回归的经验研究［J］.统计与信息论坛，2011，26（11）：50－57.

［8］Koenker R，Bassett G W.Regression quantiles［J］.Econometrica，1987，46（1）：33－50.

［9］叶五一，缪柏其，谭常春.基于分位点回归模型变点检测的金融传染分析［J］.数量经济技术经济研究，2007（10）：151－160.

［10］陈建宝，杜小敏，董海龙.基于分位数回归的中国居民收入和消费的实证分析［J］.统计与信息论坛，2009，24（7）：44－50.

［11］李顺毅.房价如何影响消费对经济增长的贡献：基于分位数回归的实证分析［J］.消费经济，2011，27（3）：3－10.

［12］魏亮瑜，凌能祥，李成好.基于遍历函数型数据条件分位数估计的相合性［J］.合肥工业大学学报：自然科学版，2012，35（4）：557－562.

［13］Sohn I，KiMS，Hwang C，et al.Support vector machine quantile regression for detecting differentially expressed genes in microarray analysis［J］.Method of Information in Medicine，2008，47（5）：459－467.

［14］Munir Said，Chen Haibo，Ropkins Karl.Modelling the impact of road traffic on ground level ozone concentration using aquantile regression approach［J］.Atmospheric Environment，2012，60：283－291.

［15］公安部消防局.中国火灾统计年鉴 ［M］.北京：中国人民公安大学出版社，1997：66－77.

［16］公安部消防局.中国消防年鉴［M］.北京：中国人事出版社，2004：88－96.