T形钢管混凝土柱荷载－位移骨架曲线模型

曹 兵， 黄 俊， 戴绍斌

（1.武汉理工大学 土木工程与建筑学院，湖北 武汉 430070；2.武汉理工大学 建筑设计研究院，湖北 武汉 430070）

低周反复荷载作用下构件的恢复力特性通常用滞回曲线和骨架曲线来表示，滞回曲线反映了构件在反复荷载作用下的变形过程，而骨架曲线则直接地反映了构件在反复荷载作用下所经历的损伤历程［1］。低周反复荷载作用下，滞回曲线峰值点的连线（外包线）即为骨架曲线，它与一次性加载曲线相接近。骨架曲线上能够反映出结构或构件的屈服荷载和屈服位移、极限荷载和极限位移等特征点，骨架曲线概括了结构或构件的强度、刚度、延性等力学特性，这些都是衡量结构抗震性能的重要指标［2］。

目前，对钢管混凝土柱荷载－位移骨架曲线模型的研究成果主要有：文献［3］对方形、矩形钢管混凝土构件骨架曲线进行了研究，详细描述了骨架曲线的影响因素，推导了骨架曲线模型计算参数；文献［4］对圆形钢管混凝土构件进行了研究，提出了荷载－位移骨架曲线的计算模型；文献［5］对空心圆钢管混凝土压弯构件骨架曲线进行了研究，得出了骨架曲线的影响因素并回归出了骨架曲线简化模型计算公式；文献［6］对普通钢管混凝土框架骨架曲线进行了研究，得出了骨架曲线的影响因素；文献［7］对压弯构件恢复力模型骨架曲线进行了研究，从理论上推导出了压弯构件力和变形的关系；文献［8］研究了截面宽厚比和长宽比对L形钢管混凝土柱骨架曲线的影响，得出了骨架曲线主要影响因素；文献［9］研究了改进的L形钢管混凝土柱抗震性能，提出了改进的L形钢管混凝土柱骨架曲线模型参数计算表达式；文献［10］对低周反复荷载作用下再生混凝土框架进行了试验研究，分析了荷载－位移骨架曲线的变化特点；文献［11］对方形钢管混凝土轴压柱屈曲性能进行了研究，提出了钢管屈曲时相关参数计算表达式。由此可见，对异形钢管混凝土柱荷载－位移骨架曲线的研究相对较少。

综合上述研究，影响钢管混凝土柱荷载－位移骨架曲线的因素主要有轴压比、套箍系数、长细比等。本文为了研究T形钢管混凝土柱荷载－位移骨架曲线，采用有限元软件ABAQUS对T形钢管混凝土柱在低周反复荷载作用下抗震性能进行数值分析，根据对有限元计算所得的骨架曲线形状进行对比分析，提出了骨架曲线简化模型并回归了模型参数计算表达式，最后与有限元结果进行对比，为以后的研究提供参考。

1 有限元分析模型

本文中采用有限元建模时，混凝土的单元类型选取8节点减缩积分三维实体单元（C3D8R），钢管的单元类型选取4节点四边形有限薄膜应变线性缩减积分壳体单元（S4R），柱两端边界条件取为嵌固连接，首先在柱顶部施加轴向荷载，然后在柱顶部施加位移荷载，最后取柱中部反力P和位移Δ绘制荷载－位移骨架曲线。T形钢管混凝土柱截面形式如图1所示，有限元分析模型如图2所示。试件序号与编号见表1所列。表1中，TM1－321300的TM1表示T形钢管混凝土柱有限元模型1，3表示图1中A为300mm，2表示B为200mm，1表示C为100mm，3表示D 为3mm，最后2位00表示加载方向θ为0°；其余模型数值意义依此类推。

图1 T形钢管混凝土柱截面示意图

图2 T形钢管混凝土柱有限元分析模型

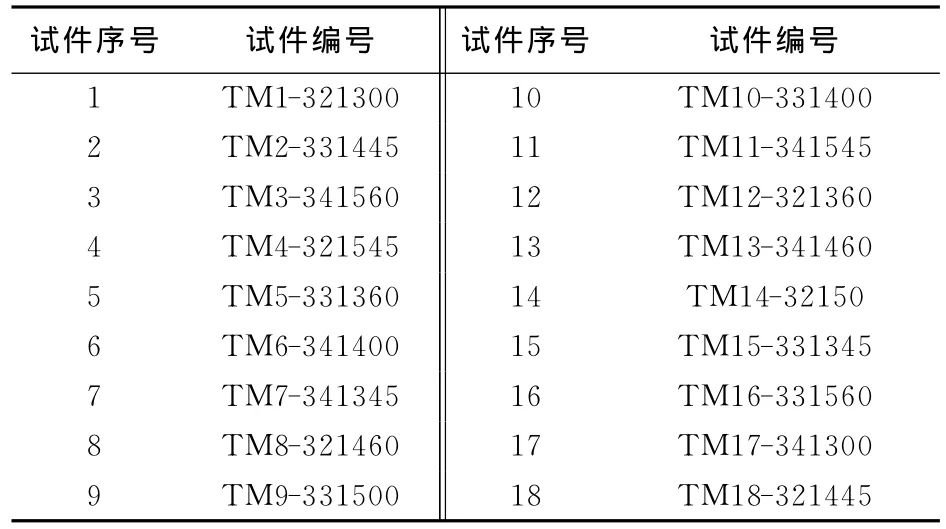
表1 试件序号与编号

2 荷载－位移骨架曲线模型

钢管混凝土压弯构件的荷载－位移骨架曲线有2种可能情况，即无下降段和有下降段，因此，骨架曲线有2种简化计算模型，即用二折线模型模拟无下降段的荷载－位移骨架曲线，用三折线模型模拟有下降段的荷载－位移骨架曲线［4］。通过对有限元计算所得的T形钢管混凝土柱荷载－位移骨架曲线进行对比分析，该曲线只有弹性阶段和强化阶段，并没有出现下降段，本文采用二折线模型来模拟有限元计算所得的荷载－位移骨架曲线，如图3所示，其中，A点为弹性阶段的终点，其相应的荷载值为Py，B点为峰值荷载点，其相应的荷载值为Pu，OA段刚度为Ka，AB段刚度为Kb。从图3可以看出，该模型需要确定的参数主要为弹性阶段的刚度Ka、屈服荷载Py和强化阶段的刚度Kb。

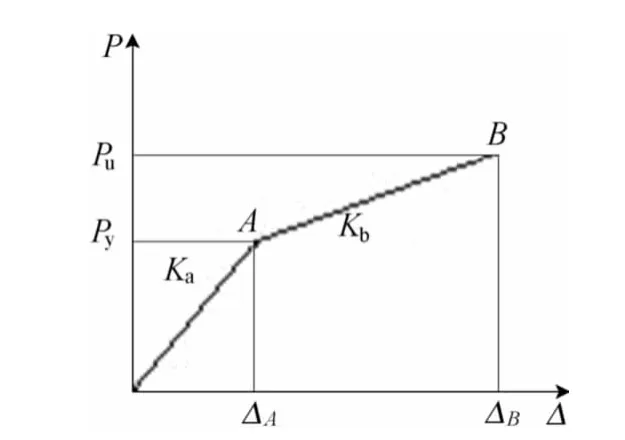
图3 荷载－位移骨架曲线计算模型

3 模型参数确定与计算结果对比

简化力学模型如图4所示。

图4 试件力学简化模型

利用数值方法计算钢管混凝土压弯构件的荷载－位移滞回关系曲线时，由于侧向荷载P和侧向位移的关系受计算长度的影响很大，对于不同的边界条件，需要合理确定构件的计算长度［12］。对于常见的在恒定轴向压力作用下的两端为嵌固支座、一端有水平侧移的框架柱，如图4a所示，其反弯点在柱的中央，可以将其简化为从反弯点到固端长度为L＝L1／2的悬臂构件，如图4b所示，并反向对称延伸。当忽略侧向荷载P对构件挠曲线形状的影响时，就可将悬臂构件等效成长度为L1＝2L的两端绞支构件，如图4c所示。

3.1 弹性阶段刚度

假设试件在图4b荷载作用下试件的挠曲线方程为Y（x），忽略轴力对试件弯矩的影响，则试件在任意处的弯矩表达式为：

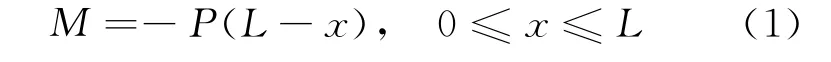
由材料力学理论可知：

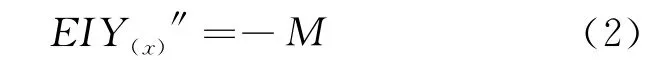
其中，EI为钢管混凝土组合抗弯刚度。

根据（1）式和（2）式可得试件的挠曲线微分方程：

对（3）式进行一次积分得：

对（4）式再一次积分得：

试件力学简化模型的边界条件为：

将（6）式代入（4）式和（5）式得：

将（7）式代入（5）式得试件挠曲线方程：

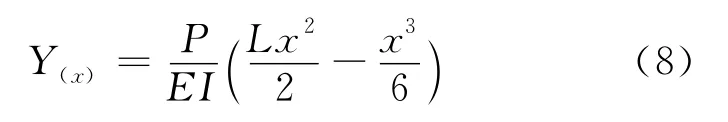
当x＝L时，（8）式取得最大值：

对公式中钢管混凝土组合抗弯刚度EI的计算，目前还没有一个统一的算法，本文采用EC4（1994）［13］中建议的计算公式：

将（10）式代入（9）式得：

由（12）式计算的弹性阶段刚度和有限元计算的相应结果见表2所列。从表2中可以看出，Ka的计算值比有限元计算值要小，这是由于没有考虑轴力的影响，因此需对（12）式进行一定的修正。本文采用最具有代表性的通过正交试验设计得出的18组有限元计算结果进行比较，统一引入修正系数η，取它们之间误差的平均值，经过计算得η＝1.366，经过修正之后所得Ka的计算公式为：

表2 弹性阶段刚度Ka计算表 kN／m

3.2 屈服荷载

参照文献［4，12］，对于图4b所示的力学简化模型，钢管混凝土悬臂柱在恒定轴向压力N作用下，对于构件端部的每一级位移Δ，其侧向荷载P都可由公式P＝（M－NΔ）／L计算，T形钢管混凝土柱骨架曲线模型屈服荷载Py计算表达式可归结为：

基于T形钢管混凝土柱骨架曲线影响参数有限元分析结果，屈服荷载主要和轴压比n、套箍系数ζ和长细比λ等因素有关，其关系曲线如图5所示。

从图5a可知，当n＜0.5时，曲线呈二次曲线变化，采用二元一次方程进行回归；当n≥0.5时，曲线呈线性变化，采用一元一次方程进行回归；从图5b可知，曲线呈线性变化，采用一元一次方程进行回归；从图5c可知，曲线呈双曲线变化，采用双曲线方程进行回归。

图5 屈服荷载随轴压比、套箍系数和长细比变化曲线

通过回归分析，得到的回归方程为：

My为屈服弯矩，其计算表达式［4］为：

My

3.3 强化阶段刚度

本文将强化阶段刚度Kb表达式［4］回归为：

基于T形钢管混凝土柱骨架曲线影响参数有限元分析结果，强化阶段刚度主要和轴压比、套箍系数和长细比等因素有关，其关系曲线如图6所示。

图6 强化阶段刚度随轴压比、套箍系数和长细比变化曲线

从图6a可知，曲线呈二次曲线变化，采用二元一次方程进行回归；从图6b可知曲线呈线性变化，采用一元一次方程进行回归；从图6c可知曲线呈二次曲线变化，采用二元一次方程进行回归。通过回归分析，得到的回归方程为：

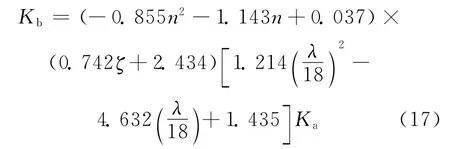
T型钢管混凝土柱屈服荷载和强化阶段刚度有限元计算值和采用回归公式的计算值见表3所列。

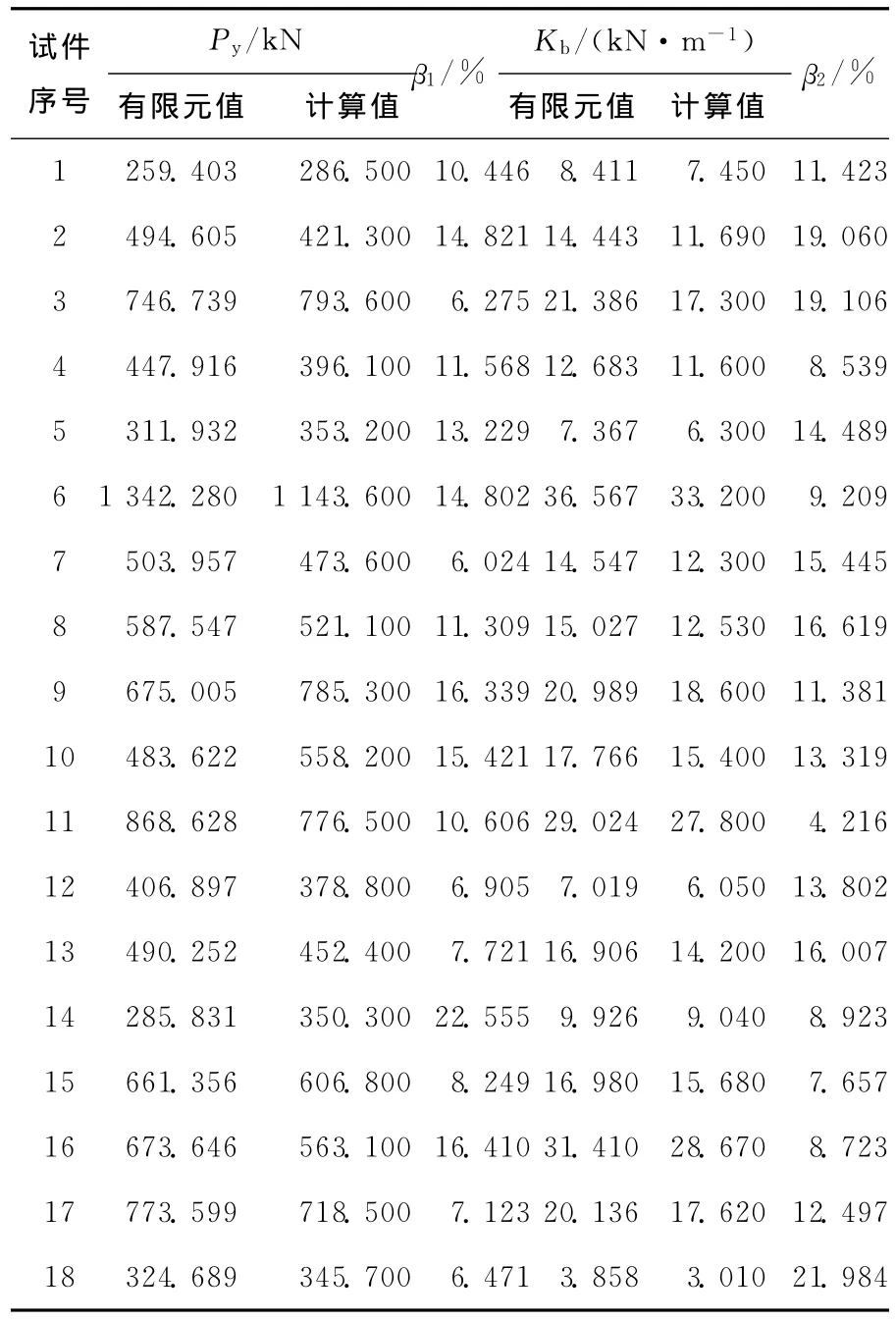
表3 屈服荷载Py和强化阶段刚度Kb计算表

3.4 骨架曲线计算结果对比分析

由二折线模型计算所得的骨架曲线与有限元计算所得骨架曲线对比如图7所示。由于篇幅的关系，只列出了3组对比模型。从图7可以看出，2条曲线吻合较好，表明所选取的二折线模型具有一定的计算精度。因此，本文所推导的二折线模型相关参数计算表达式具有一定的近似性。

图7 二折线模型和有限元骨架曲线对比

4 结 论

基于有限元计算所得T形钢管混凝土柱荷载－位移骨架曲线，根据骨架曲线的特点采用了二折线模型来模拟有限元计算所得的骨架曲线，充分考虑了轴压比、套箍系数、长细比对骨架曲线的影响，推导出了二折线模型相关参数计算表达式。最后，将二折线模型计算骨架曲线与有限元计算骨架曲线进行了对比，可以得到如下结论：

（1）弹性阶段刚度有限元计算值比模型计算值偏大，引入修正系数η进行修正，修正之后误差基本控制在一定范围内。

（2）轴压比、套箍系数和长细比对屈服荷载和强化阶段刚度影响较大。屈服荷载和强化阶段刚度均随轴压比呈二次曲线变化，随套箍系数呈线性变化。屈服荷载随长细比呈双曲线变化，强化阶段刚度随长细比呈二次曲线变化。

（3）采用二折线模型计算所得骨架曲线与有限元计算所得骨架曲线吻合程度较好，该模型具有一定的计算精度和应用价值。

［1］刁 波，李淑春，叶英华.反复荷载作用下混凝土异形柱结构累积损伤分析及试验研究［J］.建筑结构学报，2008，29（1）：57－63.

［2］游经团，韩林海.钢管高性能混凝土压弯构件滞回性能试验研究［J］.地震工程与工程振动，2005，25（3）：98－103.

［3］韩林海，杨有福.现代钢管混凝土结构技术［M］.第2版.北京：中国建筑工业出版社，2007：244－307.

［4］钟善桐.钢管混凝土结构［M］.第3版.北京：清华大学出版社，2003；186－201.

［5］张凤亮.空心圆钢管混凝土压弯构件骨架曲线和延性系数的研究［D］.哈尔滨：哈尔滨工业大学，2008.

［6］孙修礼，梁书亭，段友利.钢管混凝土框架曲线研究［J］.地震工程与工程振动，2007，27（1）：99－103.

［7］赵忠虎.压弯构件恢复力模型骨架曲线的研究［J］.工业建筑，2007，15（9）：73－76.

［8］张继承，沈祖炎，周海军.L形钢管混凝土柱抗震性能非线性有限元分析［J］.工业建筑，2010，15（7）：85－90.

［9］李芹芹.L形钢管混凝土组合柱抗震性能有限元分析［D］.武汉：武汉大学，2010.

［10］吴 童，柳炳康，周 安，等.低周反复荷载下再生混凝土框架边节点受力性能试验研究［J］.合肥工业大学学报：自然科学版，2012，35（1）：82－85.

［11］金雪峰，张学文，蔡 健.方形钢管混凝土轴压柱局部屈曲性能的研究［J］.合肥工业大学学报：自然科学版，2007，30（7）：885－887.

［12］韩林海.钢管混凝土结构：理论与实践［M］.北京：科学出版社，2004：268－304.

［13］European Committee for Standardization.Euro－code 4：design of composite steel and concrete structures，part1.1：general rules and rules for buildings［S］.Brussels，Belgium：European Committee for Standard Institutions，1994.