基于AHP－Fuzzy综合评价法的工业厂房可靠度分析

黄慎江， 童 雪

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

0 引 言

对于建筑物的鉴定方法，一般可以分为3种：传统经验法、实用鉴定法、概率鉴定法。传统经验法是由有经验的专家通过现场观察和简单的计算分析，以原设计规范为依据，根据个人专业知识和工程经验直接对建筑物的可靠度做出评估。实用鉴定法是应用各种检测手段对建筑物及其环境进行周密的调查、检查和测试，应用计算机技术以及其他相关的技术和方法分析建筑物的性能和状态，全面分析建筑物存在问题的原因，以现行的规范为基准按照统一的鉴定程序和标准，从安全性、适用性多个方面综合评定建筑物的可靠性水平。概率鉴定法是在实用鉴定法的基础上，进一步利用统计推断方法分析影响特定建筑物可靠性的不确定因素，更直接利用可靠性理论评定建筑物的可靠性水平。目前，我国现行的民用和工业建筑可靠性鉴定标准［1－2］均是以实用鉴定法为基础，同时引入概率鉴定法的思想。

层次分析法最早是由美国的Thomas L.Saaty教授提出的，1982年他的学生H.Gholamnezhad将该方法引入了我国［3］。该方法是将决策问题按总目标、各层子目标、评价准则直至具体备投方案的顺序分解为不同的层次结构，然后用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再以加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。而AHP－Fuzzy综合评价法是一种以层次分析法为基础的评价方法。该方法能够有效地将经验和模糊数学理论结合起来，利用较少的定量信息得到精确的结果。这种简单有效的评价方法在钢筋混凝土结构可靠度的研究中也有着不可小觑的作用。

1 建立递阶层次结构模型

层次分析法的首要任务就是根据决策问题要实现的目标、评判的准则以及可供选择的方案将问题分为目标层、准则层和方案层，即把决策问题层次化，建立递阶层次结构模型［4］。文献［3］采用的是可靠度鉴定评级的方法，将安全性和适用性合并为可靠性，然后按子项、项目、单元3个层次进行评定，每个层次的可靠度水平各划分为4个等级。据此，可对某工业厂房的可靠度进行分析，建立如图1所示的递阶层次结构模型。

图1 某工业厂房可靠度分析的递阶层次结构模型

2 用AHP法确定层次指标权重

通过对问题进行分析并建立相应层次分析结构模型，问题即转化为层次中的排序计算。而最终则归结为相对于结构可靠度总目标，各评判标准相对重要性的排序［5－6］。

2.1 构造比较判断矩阵

为了使决策判断定量化，形成有效的数值判断矩阵，层次分析法引用了1～9比率标度方法［7］。根据两两因素之间重要性程度的差异，在1～9标度范围内进行定值，从而构造出比较判断矩阵。判断矩阵见表1～表5所列。

表1 A－B的判断矩阵

表2 B1－C的判断矩阵

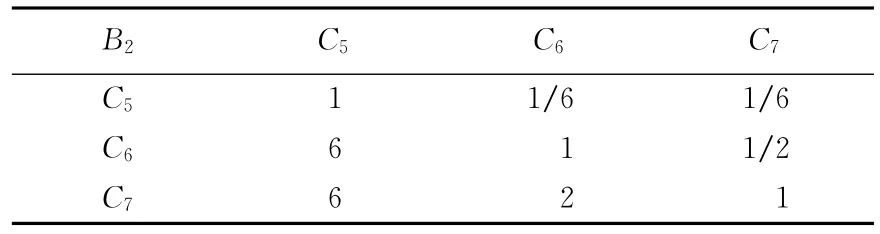
表3 B2－C的判断矩阵

表4 B3－C的判断矩阵

表5 B4－C的判断矩阵

2.2 单准则下的排序及一致性检验

根据上述各层次判断矩阵，通过计算其最大特征值和特征向量，即可计算出某层次因素相对于上一层次中某一因素的相对重要性权值，也就是进行层次单排序。然后再根据判断矩阵的一致性比率CR的值是否小于0.1来检验判断矩阵是否具有满意的一致性。

层次单排序的权重向量如下。

A－B 矩阵 ：

B1－C 矩阵：

B2－C 矩阵：

B3－C 矩阵：

B4－C 矩阵：

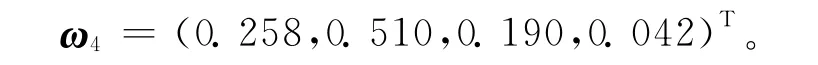
经计算，5个层次单排序的一致性指标CR值均小于0.1，具有满意的一致性。一致性检验计算结果见表6所列。

表6 一致性检验计算结果

2.3 层次总排序及一致性检验

在各层次单排序计算的基础上还需要进行各层次的总排序计算以及一致性检验，以保证分析得到的结论基本合理。

由上述计算结果可知，B层相对于总目标A的排序向量为：

C层相对于总目标的排序向量为：

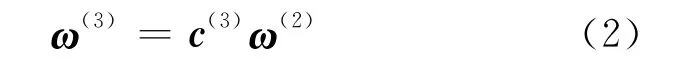
再由CI（2）、RI（2）分别计算：

最终可得：

由此可见，层次总排序满足一致性要求。

3 可靠度隶属度的确定

可靠度分析是采用模糊综合评价方法进行的，该方法是将评价指标的隶属度与权重进行模糊运算，使计算结果更加客观。可靠度等级隶属度的计算首先是采用专家打分法来确定各失效事件的影响后果C的估值及发生概率P的估值，将P与C的乘积带入失效事件对于失效等级的隶属函数，便可得到失效事件对于可靠度等级的隶属度［8］。

具体步骤如下：

（1）确定失效发生概率P的估值。失效的发生概率分为5个等级，估算方法见表7所列。

（2）确定失效影响后果C的估值。分为5个等级，估算方法见表8所列。

（3）确定失效接受准则。失效接受准则见表9所列。

表7 失效发生概率P估值

表8 失效影响后果C的估算

表9 失效接受准则

（4）隶属度值的计算。根据失效接受准则，将工业厂房结构的可靠度分为4个等级，并构造隶属度函数［6－7］，如（6）～（9）式，隶属度函数图如图2所示。将失效事件的发生概率估计值P和失效事件影响后果估计值C相乘后得到的数值带入隶属函数，便可得到该失效事件对4个等级可靠度的隶属值。一至四级可靠度下的隶属度函数如下：

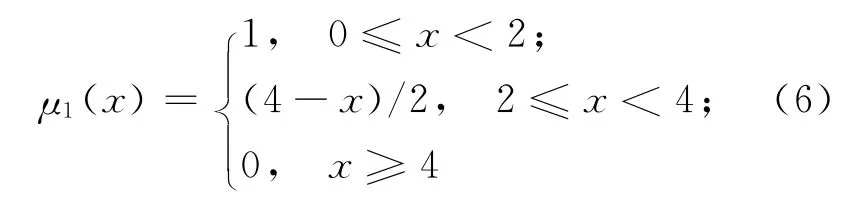
图2 隶属度函数图

4 工程实例

本文以某钢筋混凝土工业厂房为例，用AHP－Fuzzy综合评价法对其可靠性进行了分析。通过专家们对该厂房进行的现场分析和检测，对各评价项目进行估值，见表10所列。

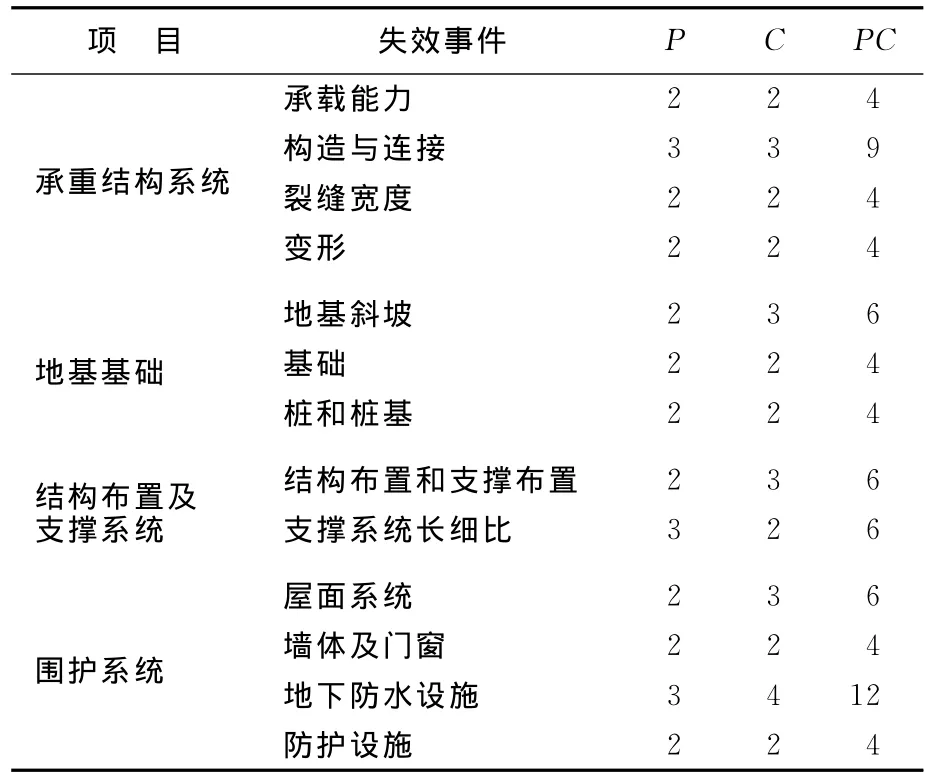
表10 评价指标的估值

再将所得PC的值代入相应的隶属函数，构造出各项目的评价矩阵：

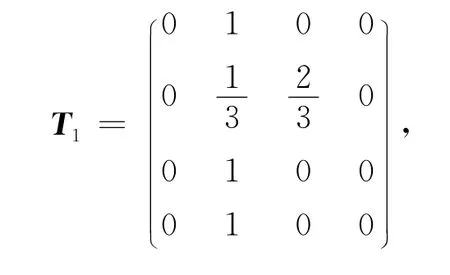
将各项目的评判矩阵与其权重向量进行模糊运算，便可得到各工序的隶属度向量：

将各项目的隶属度向量组成新的评价矩阵，将其与权重向量进行模糊运算，便可得到该结构的可靠度向量，计算结果为：

根据最大隶属度的评判标准可以看出，该厂房结构可靠度等级为二级。

5 结 论

（1）在对工业厂房的结构可靠度进行分析时，可先采用层次分析法将结构分别按子项、项目、单元3个层次进行分解，并对可能出现的失效进行分析和识别［8］。再根据专家的评判，将估值代入失效级别隶属度函数，建立评判矩阵，进行模糊评价，最后，根据最大隶属度原则确定结构总体可靠度的等级。

（2）在结构可靠度分析中，由于结构自身的复杂性以及失效事件所具有的随机性和模糊性，结构的可靠度不能用非常准确的数据加以量化表达［9］。采用AHP－Fuzzy综合评价法能够有效地对工业厂房的结构可靠度进行评估，并使得评估结果更接近实际。

（3）对于现役建筑结构可靠度的鉴定仍是一门实践性和经验性很强的工作，理论分析所得出的结果必须依赖于现场检测所得结果。建筑物的安全性既取决于设计、施工阶段所形成的先天条件，也与后天的使用、维护和监护情况密切相关。因此，建立起完善的现有结构可靠度鉴定方法和评定标准，能够为建筑物正常使用、维护和加固提供理论依据。

随着现代科学技术的发展，越来越多的分析方法被应用于结构可靠度研究之中，例如遗传算法、基于 Matlab神经网络法、改进的PNET法等［10］。这些方法对结构可靠度理论的发展都起到了不同程度的推进作用。

［1］GB 50292－1999，民用建筑可靠性鉴定标准［S］.

［2］GBJ 144－2008，工业建筑可靠性鉴定标准［S］.

［3］赵焕臣，许树柏，和金生.层次分析法：一种简易的新决策方法［M］.北京：科学出版社，1986：2－28.

［4］王忠文，马永欣，于 峰.钢筋混凝土结构可靠性模糊综合评估［J］.交通科技与经济，2008，10（1）：1－3.

［5］李柏年.模糊数学及其应用［M］.合肥：合肥工业大学出版社，2007：103－134.

［6］赵国藩，金伟良，贡金鑫.结构可靠度理论［M］.北京：中国建筑工业出版社，2000：65－72.

［7］黄慎江，何丽丽.AHP－Fuzzy综合评价法在高层结构量化选型中的运用［J］.合肥工业大学学报：自然科学版，2012，35（9）：1243－1247.

［8］张吉军.模糊层次分析法（FAHP）［J］.模糊系统与数学，2000，14（2）：80－88.

［9］薛 勇，李宾强，马 龙，等.模糊综合法在结构设计中的应用［J］.低温建筑技术，2012（1）：39－41.

［10］李远瑛，张德生.基于MATLAB的结构可靠度分析方法研究［J］.嘉应学院学报，2011，29（2）：45－48.