高强化柴油机曲轴过渡圆角应力计算的研究

李 文，廖日东，左正兴，刘丽涛

(1.北京控制工程研究所，北京 100190; 2.北京理工大学机械与车辆学院，北京 100081)

前言

随着柴油机强化程度的不断提高，曲轴的工作条件愈加苛刻。众多实验和数值计算表明［1-3］，曲轴最大应力的位置处于与发火气缸相对应的连杆轴颈或主轴颈的两端过渡圆角区域。为了准确进行曲轴的强度可靠性评估，有效制定曲轴过渡圆角区域的强化工艺措施，须对工作状态下过渡圆角的应力分布情况进行详细分析［4-6］。曲轴过渡圆角区域的应力分布情况很难通过实验的方法准确测量［7］，有限元法是目前曲轴应力计算的常用方法。

使用有限元方法进行计算的关键是尽可能减小计算误差。文献中针对提高曲轴强度计算准确性的研究大多集中在模型的结构简化和边界条件施加的正确性方面。文献［8］中使用连续梁法计算所得弯矩和支反力作为边界条件对忽略油孔的曲轴单拐进行了静力学计算，文献［9］中通过使用曲轴整轴有限元模型提高了静计算结果的精度，文献［10］中通过使用弹簧单元模拟轴承的支撑作用，使边界条件符合实际条件。许多文献还进一步从曲轴结构的动力学、摩擦学角度对曲轴结构强度进行研究［11-12］。然而，这些工作并没有深入研究有限元方法计算误差对结果的影响。

实际上，有限元模型的离散模式也是影响计算结果收敛性的重要因素。因此，本文中以某型号高强化柴油机曲轴为研究对象，在采用合理的模型简化和边界条件施加方式的同时，考虑了有限元计算结果在曲轴过渡圆角应力集中区域的收敛性，以期获得曲轴过渡圆角网格划分形式与分析精度的关系，降低计算结果的误差，并在此准则的基础上建立了具有良好计算收敛性和稳定性的曲轴模型。

1 曲轴单拐及其简化模型

1.1 曲轴单拐的有限元模型

曲轴单拐结构复杂，在工作过程中承受弯矩、转矩和轴向力的联合作用，但主要是爆发压力造成的冲击力。曲轴失效的基本形式是弯曲疲劳失效和扭转疲劳失效，其中弯曲疲劳失效占曲轴失效的80%，因此可认为通过活塞和连杆传递给连杆轴颈的气缸爆发压力和主轴颈轴承的支反力是曲轴失效的主要原因。现阶段对曲轴强度计算所采用的计算模型主要有以下两种:(1)曲轴的整体模型，该模型能够充分考虑相邻曲拐之间相互影响和给定工况下各曲拐的应力情况，但计算规模的限制使轴颈过渡圆角处无法布置足够数量的网格，以保证应力集中部位计算结果的收敛性;(2)曲轴的单拐模型，该模型通常用于分析受载最严重的曲拐，通常利用曲拐的结构和载荷的对称性，取1/2单拐作为分析对象。

由于本文中研究对象是曲轴过渡圆角区域内的应力分布，因此选取某型号柴油机1/2曲轴单拐模型进行分析，主要考虑弯曲载荷的作用。

边界条件如图1(a)所示，在对称面上施加对称约束，p为作用在连杆轴颈上的爆发压力，F1和F2是主轴颈上承受的平衡支反力。载荷沿连杆轴颈和主轴颈轴线方向按二次抛物线规律分布;沿轴颈圆周方向120°范围内按余弦规律分布［8］。

1.2 曲轴单拐过渡圆角的简化模型

为获得模型网格数量和形状函数阶数对曲轴过渡圆角区域计算结果收敛性的关系，选取图1(a)中所示的灰色区域为研究对象，将该区域简化为图1(b)所示的阶梯轴，其中R1=R3，R2=R4。根据曲轴主轴颈和连杆轴颈的过渡圆角的实际形状，简化的阶梯轴模型的过渡圆角分为沉割式(见图1(d))和非沉割式(见图1(e))。通过计算结果的对比，两种形式的过渡圆角具有相同的应力集中收敛性质。文中仅列出了非沉割式圆角收敛性的分析过程。在阶梯轴细端端面施加沿竖直方向(z方向)的面力T，相对于对圆角位置形成弯矩，不断调整该面力的大小，通过多次试算使应力峰值的大小与相同局部网格数量的曲轴单拐模型在最大爆发压力作用下的圆角应力峰值相近，便于与曲轴单拐模型的计算结果进行比较。当最大爆发压力为17MPa时，面力T的大小为42.94MPa。

2 简化模型的收敛性分析

有限元方法的计算程度与试探空间(形状函数)能否很好地局部逼近精确解息息相关［13］。在应力集中区域内的应力峰值和应力梯度比其它区域大很多，因此需要更多的网格数量或更高的多项式次数，才能获得更加逼近真值的解。为获得网格数量和形状函数阶次与应力集中区域计算结果收敛性的关系，选取图1(b)中灰色区域为网格加密区域，划分方式如图1(c)所示，使 L1=L2=L3=L4，其中L1=πr/2为过渡圆角的弧长，r为过渡圆角半径。在该区域内布置六面体网格，可以发现对于固定过渡圆角半径和轴颈半径的阶梯轴，影响网格尺寸的变量一共有3个，分别是沿过渡圆角周向α的网格数m，过渡圆角深度方向ρ1的网格数n，轴颈周向φ的网格数l。本文中将通过一系列计算与分析对m、n、l的取值与结果收敛性进行讨论。本文中所有有限元计算均使用ABAQUS standard求解器进行求解。计算中弹性模量E=210GPa，泊松比ν=0.3。

2.1 m，n取值对结果收敛性的影响

分别变化m和n值得到应力集中处的Mises应力值，见表1。由表可见:m一定时，随着n的不断增大，应力集中点处的应力峰值不断增大;n一定时，改变周向网格数m，当m＜6时，应力峰值随着m值增加而迅速增大;当m≥6时，随着周向网格数的增加，最大应力峰值在一定范围内波动。因此，过渡圆角周向网格数m≥6时，网格数的增加对结果收敛性的影响较小。应力值的小幅变化是由于过渡圆角周向网格数目的增加引起的节点位置变化造成的。可见过渡圆角深度方向网格数是决定应力峰值收敛性的主要因素。

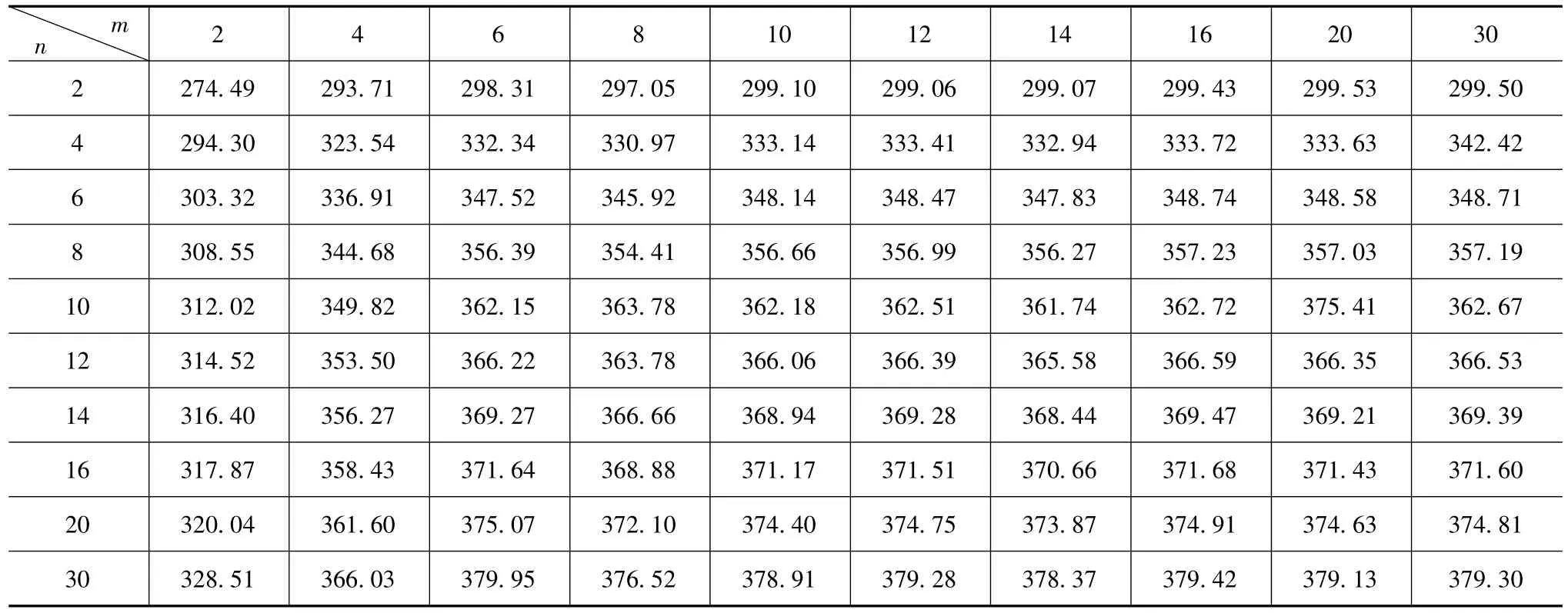
表1 过渡圆角处m，n取值与最大Mises应力σAmax的关系MPa

在模型建立过程中，单元质量也是必须考虑的重要因素。低质量的网格单元会造成较大的计算误差或结果的不收敛，因此n与m不宜相差过大。通常情况下，当n=m时能获得较好的网格单元质量。

由表1可以得到网格数与收敛误差的关系。将m与n均为30时的最大应力值379.30MPa作为基准，可以发现对于六面体一次单元，当m与n均为6时即可满足工程上误差为10%的要求;当m与n均划分为10，即可满足工程上误差为5%以内的高精度要求。

2.2 l取值对结果收敛性的影响

固定m和n值(m=n=12)，改变 l值，可算得过渡圆角区域中的应力峰值σAmax，如表2所示。当该结构仅承受弯矩作用时，过渡圆角处的最大应力值随l值的变化并不显著。当l值由72变为6时，应力只提高了0.49%。故可认为，在保证单元质量的前提下，轴颈周向网格数对结果不产生显著影响。

表2 m与n为12时环向网格密度变化时的最大Mises应力σAmax MPa

2.3 收敛准则的适用性分析

为讨论上述收敛性准则对不同圆角几何尺寸的适用性，保持边界条件和网格划分方式不变，改变过渡圆角半径r，令m=n且将其数值从2逐渐增加至30，可以获得r取值不同时网格数量与应力峰值的关系，如表3所示。由表可见:圆角半径r取值的不同改变了应力峰值的大小，但通过对表3的数据进行归一化处理发现，随着r取值不同网格划分数量与结果收敛性的关系并没有多大变化，说明所获得的收敛性准则适用于不同尺寸的过渡圆角。

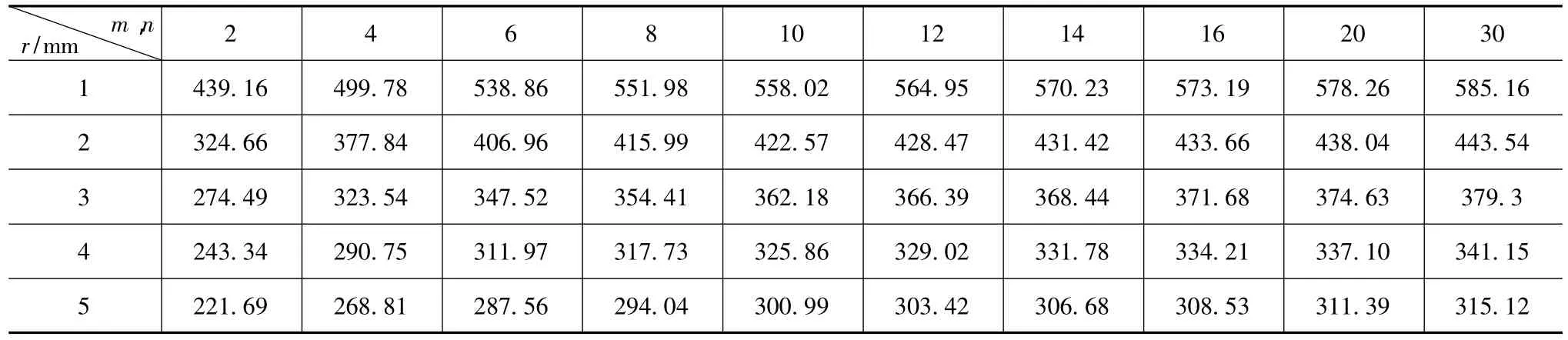
表3 m与n相等时，圆角半径与最大Mises应力σAmax 的关系 MPa

3 阶梯轴与曲轴单拐的应力对比

应力集中造成的数值计算误差主要是由于高应力梯度造成的。为了证明由阶梯轴模型得到的过渡圆角区域承受弯矩作用时收敛准则能够适用于曲轴单拐，将阶梯轴与曲轴单拐的过渡圆角处应力分布与应力梯度进行对比。其中阶梯轴模型的过渡圆角分为沉割式和普通式两种。

曲轴单拐过渡圆角采取与阶梯轴相同的区域选择和划分方式，且阶梯轴的轴颈半径与过渡圆角半径之比和曲轴单拐主轴颈与过渡圆角之比相同。为了获得较好的收敛性，曲轴单拐和阶梯轴的过渡圆角周向网格数和深度方向网格数均取12，并且严格控制过渡圆角区域处的节点位置，在过渡圆角区域分别建立局部坐标系O3和O4，如图2所示。

选取应力峰值点处的沿过渡圆角周向、深度方向和轴颈周向的应力分布进行对比，可以发现以下规律。

(1)无论是沉割式还是普通过渡圆角，在过渡圆角表面，阶梯轴和曲轴单拐沿过渡圆角周向的应力分布曲线形状相同，但应力峰值的位置不同，如图3(a)所示。

(2)在由应力峰值点为起点的沿过渡圆角深度方向ρ1的路径上，沉割式过渡圆角与普通过渡圆角的应力分布曲线基本重合，如图3(b)所示。应力值由过渡圆角表面沿ρ1方向迅速降低，曲轴单拐过渡圆角应力峰值的应力分布曲线与阶梯轴的应力分布曲线整体趋势相同，应力的下降速度稍快于阶梯轴。

(3)在以应力峰值点为起点的沿轴颈周向φ的路径上，沉割式过渡圆角与普通过渡圆角的应力分布曲线完全重合，与曲轴单拐过渡圆角的应力分布差别较大，如图3(c)所示。

(4)将阶梯轴和曲轴单拐过渡圆角区域的应力梯度进行对比，如图3(d)所示，选取各模型过渡圆角应力峰值点处沿轴颈周向、过渡圆角周向和深度方向的应力曲线，求其沿各自方向的梯度。应力梯度的计算公式为

式中:q为路径方向，qi为路径q上的单元节点，σqi为节点qi处的Mises应力值，li为节点i至路径原点处的路径长度。由于各个方向的路径长度相差较大，为便于将各方向的应力梯度进行对比，选取lqi/lq作为横坐标，Kqi值为纵坐标，其中lq为q方向的路径总长度。通过对比可以发现，沿轴颈周向，各模型的应力梯度远远小于过渡圆角周向和深度方向的应力梯度;沿过渡圆角周向，各模型的应力梯度值为幅值在251.4～-231.18MPa/mm之间连续变化的曲线;沿过渡圆角深度方向，各模型的应力梯度曲线均为一条单调递减曲线，且其应力峰值基本相同。

由上述规律可以得到以下结论。

(1)曲轴单拐模型和其过渡圆角区域的简化模型在弯矩作用下，除了在过渡圆角周向上应力集中点位置不同之外，沿各方向的应力分布曲线较为接近，且沿各方向应力梯度水平分别相同。

(2)沉割式阶梯轴模型和普通阶梯轴模型在弯矩作用下，除了在过渡圆角周向上应力集中点位置不同之外，沿各方向的应力分布和应力梯度分布基本相同。因此，在研究过渡圆角应力集中区域收敛性的过程中，将沉割式阶梯轴简化为普通阶梯轴是合理的。

(3)各模型沿轴颈周向的应力梯度远远小于其它两个方向，因此在该方向的网格分布数量对结果的收敛性基本不产生影响，与2.2节中的数值试验结果相符。

(4)各模型沿过渡圆角深度方向的应力梯度峰值远远大于其它两个方向，且应力梯度本身的变化率也较大，因此在该方向的网格分布数量是影响结果的收敛性的主要因素，与2.1节中的数值试验结果相符。

因此，由阶梯轴模型得到的弯曲载荷作用下的过渡圆角区域网格收敛性准则适用于曲轴单拐主轴颈过渡圆角区域和连杆轴颈过渡圆角区域。

4 曲轴单拐应力分布特征

由上节结论可知，过渡圆角区域周向和深度方向网格数均为12时的1/2曲轴单拐有限元模型具有较高的计算精度，因此，采用该网格划分方式对上文所研究曲轴的主轴颈和连杆轴颈过渡圆角区域的应力分布情况进行分析。

4.1 主轴颈和连杆轴颈过渡圆角应力比较

图4为该曲轴单拐在载荷作用下的Mises应力分布情况。由图可见，过渡圆角区域的应力水平较高，其中主轴颈过渡圆角位置承受压应力，连杆轴颈过渡圆角位置承受拉应力。

图5(a)中曲线是在主轴颈过渡圆角圆心处的局部坐标系O3下，0＜β＜160°范围内，距过渡圆角表面0～3mm范围内(3mm＜ρ2＜6mm)的应力分布情况;图5(b)中曲线是在连杆轴颈过渡圆角圆心处的局部坐标系O4下，0＜γ＜90°范围内，距过渡圆角表面0～3mm范围内(3mm＜ρ3＜6mm)的应力分布情况，其应力梯度的分布趋势与图5(a)中的应力分布趋势类似，但是其应力梯度与应力峰值均小于图5(a)中的应力分布曲线。由此可以得出，在过渡圆角周向方向，主轴颈过渡圆角的应力集中较为严重。

为了进一步研究应力沿曲轴过渡圆角表面深度方向的变化情况，分别对主轴颈过渡圆角表面和连杆轴颈过渡圆角表面沿深度方向选取13条路径，得到过渡圆角不同位置处的沿深度方向的应力分布曲线，见图5(c)和图5(d)。经过对比可以发现:主轴颈过渡圆角区域在表面处的应力值最大，随着深度增加应力迅速减小，在距离表面3～4mm处降至较低水平，随后应力值变化趋于平缓。连杆轴颈过渡圆角区域与主轴颈过渡圆角区域的应力分布情况类似，但是其应力峰值较低。

图5(e)中的曲线为过渡圆角表面Mises应力沿主轴颈周向的应力分布情况。应力值在φ=0～90°范围内较大，在φ=90°～180°范围内较小。图5(f)中的曲线为过渡圆角表面Mises应力沿连杆轴颈周向的应力分布情况。应力集中发生在γ=37.5°，θ=180°处，在 θ=0～110°范围内，由于外载荷的作用，存在一定程度的应力变化，在θ=110°～180°范围内应力较大，并且在θ=180°处达到应力最大值。

4.2 主轴颈和连杆轴颈过渡圆角处的应力梯度

选取主轴颈和连杆轴颈过渡圆角应力峰值点处沿轴颈周向、过渡圆角周向和过渡圆角深度方向的应力曲线，使用式(3)求其沿各自方向的梯度，如图6所示。

Kφ和Kθ为主轴颈和连杆轴颈周向的应力梯度。其中|Kφ|的最大值为15.034MPa/mm，|Kθ|最大值为15.788MPa/mm。Kβ和Kγ分别为主轴颈和连杆轴颈过渡圆角周向的应力梯度，其中Kβ为一条幅值在200.73～-231.18MPa/mm之间连续变化的曲线;Kγ是一条单调递减的曲线，其最大值为165.09MPa/mm，最小值为 -155.13MPa/mm，两条曲线的应力梯度峰值相差不大，但是由于受力状态不同，其应力梯度分布形式不同。Kρ2和Kρ3为两条单调递增曲线，其中Kρ2最小值为-526.75MPa/mm，Kρ3最小值为-349.26MPa/mm，两条曲线快速增加至-100MPa/mm之后缓慢上升并趋向于0。

由于连杆轴颈沿各方向的应力梯度与主轴颈的应力梯度水平相差不大，因此得到的各方向网格数与收敛性的关系也适用于连杆轴颈。

进一步对应力梯度的研究可以发现，沿路径方向，Kρ2和 Kρ3逐渐趋近于零，而 Kβ和 Kγ在路径两端的幅值较大，其中Kγ在路径的两端分别取最大值和最小值，说明图2中所示的网格区域并未完全包括该结构的大应力梯度区域，因此须扩大网格细化区域。由于正六面体网格的收敛性最好，因此选取图1(c)中与圆角区域相接的正方形区域进行网格细化，保证各方向网格数相同，使网格为正方形。经过分析发现，该区域在曲轴内部的边界上应力梯度很小，因此可以认为，本文中选取的网格细化区域是合理有效的。

4.3 曲轴过渡圆角各方向应力分布表达式

由图5(e)可知，沿主轴颈表面周向，φ=0截面上的应力水平最高，且此处沿轴颈周向的应力梯度最小，因此对该截面的应力分布进行研究。在极坐标系 O3下，10°≤β≤160°，3mm≤ρ2≤6mm 范围内，假设法向力和切向力的分布可表示为如下的傅里叶级数:

使用MATLAB对以上各式进行数据拟合，通过多次试算，确定此处n=1时，以上各式能够较好地表现过渡圆角区域内的法向力和切向力的分布。因此该模型过渡圆角处的法向力和切向力分布为

式中:A0，A1，B1，C0，C1，D1，E0，E1，F1为 r/ρ2和 σm的函数，ωβ，ωρ2，ωβρ2为 r/ρ2的函数;σm为假设连杆=轴颈承受均布载荷时的等效外载荷，即σm通过计算可得该型曲轴的σm=70.4887MPa/mm2;r=3mm为主轴颈过渡圆角半径。

当 ρ2分别取3，3.5，4，4.5，5，5.5，6mm 时，取过渡圆角周向均匀分布的12个节点上的应力值，对式(7)～式(9)进行数值拟合，得到ρ2不同时各式的参数取值。数据点与拟合公式的相关程度使用相关系数平方δ2表示，如表4所示。由表4可以看出，拟合的应力函数与数据点具有很好的相关性。因此，可以认为采用傅里叶级数展开的形式表示曲轴过渡圆角法向力和切向力的分布是合理的。对式(7)～式(9)中的各参数以r/ρ2

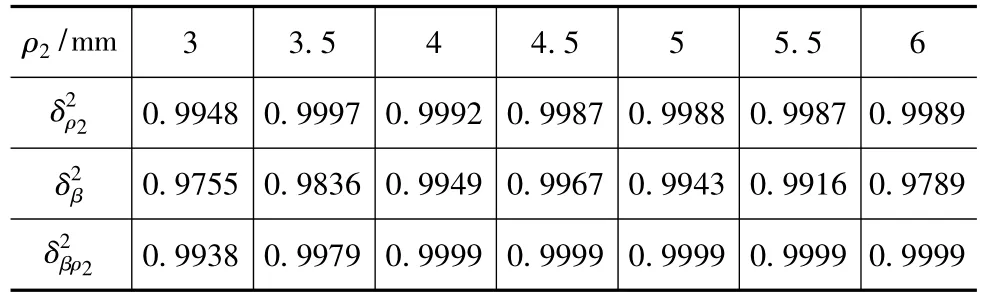
表4 主轴颈应力分布的相关性系数平方

为变量采用多项式形式进行拟合，得到各参数的多项式形式的表达式为

拟合所得表达式与数据点之间的关系通过相关系数平方δ2表示，如表5所示。由表5可知，拟合的参数表达式与数据点具有很好的相关性，表达式与数据点间的偏差较小。同样的方法可以表示连杆轴颈过渡圆角的应力分布。

表5 主轴颈应力分布各参数拟合的相关性系数平方

由于曲柄臂厚度、轴颈重合度等几何参数的影响，不同曲轴的连杆轴颈过渡圆角和主轴颈过渡圆角的相互影响程度各不相同。本文中虽然仅针对某一特定曲轴进行了讨论，但所得到的规律具有一定的参考价值，针对不同几何特征尺寸的曲轴均可以采用上述方法进行具体的研究，从而获得准确的应力分布表达式。

5 结论

(1)对于曲轴过渡圆角区域应力值的有限元计算，网格模型应采用以下收敛性准则:过渡圆角及其周围一定区域必须进行网格细化;过渡圆角周向网格数取值应该大于等于6，过渡圆角深度方向网格数应大于或等于过渡圆角周向网格数，周向与深度方向网格数均划分为10时即可满足工程上误差为5%以内的高精度要求;曲轴轴颈周向网格数对过渡圆角区域的应力逼近特性不产生显著影响，在保证单元质量的前提下，可使用较少的网格数。

(2)对于本文中使用的高强化柴油机曲轴模型，主轴颈和连杆轴颈过渡圆角区域应力峰值所在截面的各方向应力分布可使用以过渡圆角角度为变量的一次傅里叶级数的形式表示，其表达式和数据点的相关性较好。

(3)该研究方法能够运用于其他结构应力集中位置的收敛性分析，通过拟合得到的危险截面过渡圆角区域各方向应力的表达式的方法可广泛应用于曲轴过渡圆角区域强化工艺方面的研究。

［1］Osman A.Failure Analysis of a Crankshaft Made from Ductile Cast Iron［J］.Engineering Failure Analysis，2006，13:1260-1267.

［2］Pandey R K.Failure of Diesel Engine Crankshafts［J］.Eng Fail Anal，2003，10:165-175.

［3］Yu Z，Xu X.Failure Analysis of a Diesel Engine Crankshaft［J］.Eng Fail Anal，2005，12:487-495.

［4］Choi K S，Pan J.Simulations of Stress Distributions in Crankshaft Sections Under Fillet Rolling and Bending Fatigue Tests［J］.Int J Fatigue，2009，31:544-557.

［5］Ren W，Li K，Lee Y.Optical Measurement of Residual Stress at the Deep-rolled Crankshaft Fillet［C］.SAE Paper 2004-01-1500.

［6］Guo Y B，Barkey M E.FE-Simulation of the Effects of Machininginduced Residual Stress Profile on Rolling Contact of Hard Machined Components［J］.Int J Mech Sci，2004，46:371-388.

［7］Lee Y L，Morrissey W.Uncertainties of Experimental Crankshaft Fatigue Strength Assessment［J］.Int J Mater.Prod.Tech，2001，16:379-392.

［8］尹建民，王德海，袁银南.X6135柴油机曲轴强度的三维有限元研究［J］.内燃机工程，1997(2):71-77.

［9］冯国胜，张幽彤，张玉申.柴油机曲轴静动特性的三维有限元分析［J］.内燃机工程，2003，24(2):73-77.

［10］沈海涛，郑水英，李志海.基于弹簧支承的柴油机曲轴强度有限元分析［J］.机械强度，2007，29(1):161-164.

［11］Zissimos P M.A Crankshaft System Model for Structure Dynamic Analysis of Internal Combustion Engines［J］.Computers and Structures，2001，79:2009-2027.

［12］何芝仙，桂长林，李震，等.计入轴瓦变形的曲轴动应力和疲劳强度计算［J］.机械工程学报，2009，45(11):91-97.

［13］Kelly D W，De J P，Gago S R.A Posteriori Error Analysis and Adaptive Processes in the Finite Element Method:Part I-Error A-nalysis［J］.Int J Num Meth Eng，1983，19:1621-1656.