悬架下摆臂的疲劳寿命分析*

史建鹏，管 欣

(1.东风汽车公司技术中心，武汉 430058 2.吉林大学，汽车动态模拟国家重点实验室，长春 130025)

前言

关于下摆臂疲劳寿命的研究主要包括:应用结构有限元方法提升部件疲劳寿命和以台架试验为基础的多轴向疲劳寿命加载模式的分析方法。在应用结构有限元方法提升部件疲劳寿命的分析［1-2］中，通常未考虑下摆臂在车辆实际行驶工况中所受的载荷［3］，难以准确预测和设计其疲劳寿命［4］;在以台架试验为基础的多轴向疲劳寿命加载模式的分析［5］中缺少理论支持［6］，不能较好地指导下摆臂的设计。

本文中根据极限静载工况下结构应力、道路载荷作用下的下摆臂疲劳损伤和常用行驶工况下的疲劳寿命等的分析，应用CAE与台架试验分析技术和疲劳理论，采用一体化疲劳寿命分析方法，从多体动力学得到载荷值，应用“惯性释放法”获得不同工况下的下摆臂应力分布特征;据此确定易出现疲劳受损的部位，进行疲劳寿命分析，使产品达到产品的疲劳寿命要求。

1 随机载荷激励的疲劳分析机理

汽车行驶时所受载荷主要源于路面的不平度。悬架系统的下摆臂主要承受由汽车加速、减速、转弯和跳动引起的x、y、z向的力和力矩(x:汽车行驶方向;y:汽车的侧向;z:汽车的垂向)，即传递作用在车轮和车身之间的力和力矩［7］，因而承受着动应力的作用，属于疲劳寿命问题。对于下摆臂的疲劳强度，可根据应力的功率谱密度计算出疲劳损伤值［8］。

如果用铅垂平面与路面相交而得到的交线可以代表路面的不平度随路程的变化曲线，则通常是一个平稳的随机过程，该过程的统计特征可用路面激励谱密度直接表示为

式中:Dq为不平度方值;α为与Sq(ω)相应的相关函数的衰减系数;v为车速;ω为汽车在随机路面上行驶的频域值。

由于汽车悬架系统在路面不平激励下，下摆臂所受载荷在许多情况下可看成是线性系统的输入和输出问题。下摆臂传递函数可定义为初始条件为零时系统输出与输入的拉式变换之比，即

式中:H(p)为传递函数;Z(p)为输出拉氏变换;Q(p)为输入拉氏变换。用jω代替式(2)中的算子p即可得到线性系统传递特性的频率响应函数，即

当汽车行驶在良好的铺装路面上时，可近似地认为下摆臂的输入是均值为零的平稳各态历经随机过程，当其功率谱密度为Sq(ω)时，输出的随机过程的功率谱密度Sz(ω)可表示为

因而只要得到输入功率谱密度和系统的频率响应函数，就能方便地求出输出过程的功率谱密度。应用这些特征可进行下摆臂的疲劳寿命分析，文献［8］中研究表明:零件疲劳强度取决于应力的波动、顺序和频次。对于随机变动应力波形，这3个因素是随机变化的，故为了定量地研究三者对疲劳强度的影响程度，须对疲劳损伤值进行分析，具体疲劳损伤值 Dsa为

式中A为下摆臂的结构参数。

2 一体化疲劳寿命分析

随着CAE分析技术的进步和疲劳理论［9-11］的发展，零部件的强度设计由原来的主要依据静强度指标和无限寿命设计，发展到产品有限寿命设计，大大提高了产品的使用可靠性，降低了产品的开发成本。本文中采用一体化疲劳寿命分析方法，根据极限静载工况下的结构应力、道路载荷作用下的下摆臂疲劳损伤和常用行驶工况下的疲劳寿命等分析得到了试验与仿真相结合的下摆臂疲劳寿命的预测方法。

2.1 结构应力分析

在汽车行驶的常用工况下，往往会遇到一些极限行驶的环境。具体的极限静载工况主要有:车辆满载静态时，受到的垂向力;驶过凹坑或凸坎时，车轮受到冲击后，作用在下摆臂上的垂向力;在制动工况下，车辆受到的最大纵向制动力;当车辆转向时，由于离心力的影响，作用在下摆臂上的侧向力。在保证车辆与实际行驶工况一致的条件下，确定极限工况下的下摆臂所受的疲劳载荷和约束，具体载荷状况见表1。

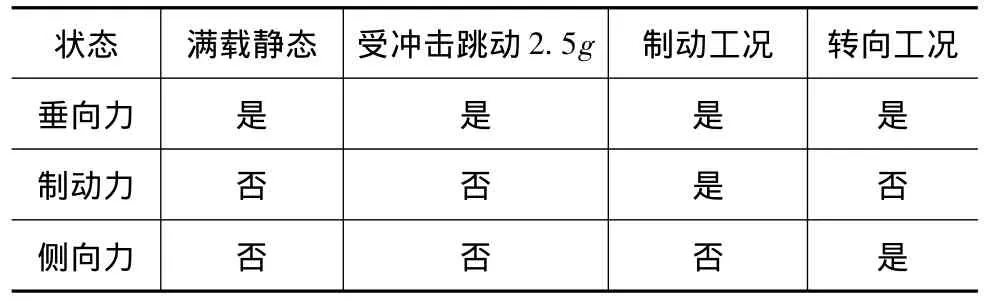
表1 极限静载工况

根据下摆臂受到的极限静载工况，结构应力分以下4种工况进行分析，分析模型如图1所示。

(1)静(稳)态工况 汽车处于满载静止状态时，下摆臂的应力分析主要是核查计算所用的模型和约束与载荷的施加是否能得到具有工程意义的结果。

(2)车轮上、下受冲击跳动2.5g工况 汽车簧上质量有2.5g加速度的状况下，下摆臂应处于上极限位置。

(3)制动工况 整车以最大减速度制动时，由于惯性力的作用，汽车的轴荷发生变化，在下摆臂的应力分析中，制动减速度引起的轴荷转移使前驱动轴的轴荷增大了25.6%。

(4)转向工况 整车急转向时，侧向加速度0.7g工况下，前(后)轴荷大部分转移到一侧的车轮上，同时整个悬架系统承受侧向力。

根据载荷情况，应用“惯性释放法”，对下摆臂进行结构应力分析。由于下摆臂结构复杂，小特征较多，故建模中采用四面体网格进行划分。在几何清理中，缝合未封闭的面、压制短线、合并小面，避免局部小特征造成不能进行网格划分的困难。为提高建模精度［12］，在经过多次试划分的基础上，选取较小的单元尺寸(2～6mm)［13-14］，并对倒角和曲率变化的地方进行细化，提高有限元模型与几何模型的一致性。

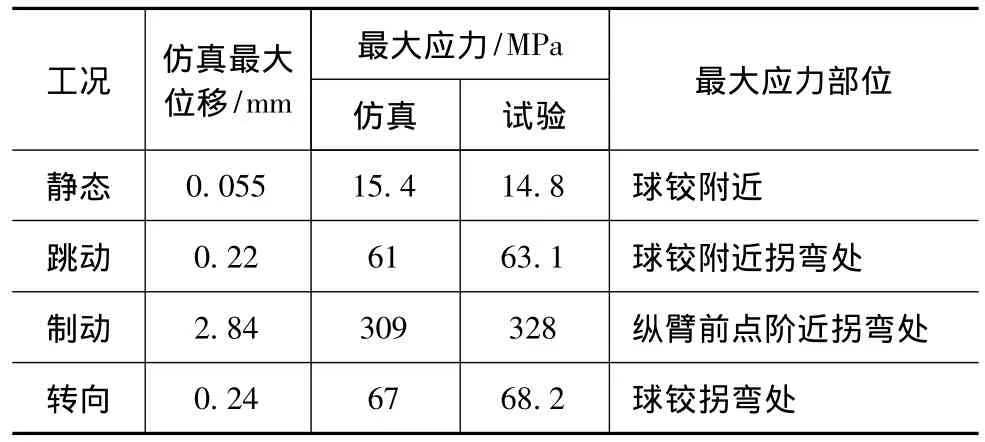
表2 结构应力仿真和试验的对比

根据确定的4种载荷工况对下摆臂进行具体的分析，结果如图2～图5所示。仿真和试验的对比结果如表2所示。由表2可以得出:只有在制动工况时，下摆臂的应力接近屈服极限，最大值为309MPa，且发生了较大变形，达到2.84mm;而其它3种工况下大多数部位的应力都远小于屈服极限。因此，下摆臂的结构强度符合设计要求，该结果为其疲劳寿命分析提供了输入应力的依据。

2.2 道路载荷作用下的下摆臂疲劳损伤分析

通过对结构在极限静载工况下的应力分析，可得到结构件的几何属性、载荷敏感部位和安全系数。但由于在静载分析时边界条件考虑不全，以致实际结构件易出现疲劳破坏的部位并非应力最大处。因此，结构件还须进行疲劳寿命分析。计算疲劳寿命的方法有很多种，其中名义应力有限寿命设计法考虑了各种系数与基本材料对零件寿命影响的疲劳特性，是一种应用较为广泛的分析方法。有限寿命设计的应力一般都高于疲劳极限，这时就不能只考虑最高应力，而须按照一定的累积损伤理论估算总的疲劳损伤［9-10］。

下摆臂在整个使用寿命里程的疲劳载荷的l级单参数雨流矩阵为

相应的疲劳损伤矩阵为

该零件在疲劳载荷作用下的总损伤为

式中:Fi为第i级载荷;Ni为第i级载荷的循环次数;c为疲劳强度系数;m为疲劳强度指数。

2.3 常用行驶工况下的疲劳寿命分析

根据结构应力分析可知，各种极限静载工况下，下摆臂的应力在材料的线弹性范围内，故汽车在行驶过程中，引起结构件断裂的是常用行驶工况下产生的重复应力，属于结构件疲劳范畴。

由于疲劳寿命主要是反映材料疲劳抗力的指标，取决于材料的强度。疲劳破坏起源的部位，经常出现在结构件的应力集中处和构件表面。下摆臂在循环载荷作用下会产生疲劳破坏［10-12］。

下摆臂所用材料的 S-N特性曲线［15］如图6所示。

分析外载荷对下摆臂疲劳寿命的影响因素，当下摆臂受到4.2(单轮离地工况)、4.0和3.8kN等大小不同的冲击载荷时，所产生的平均疲劳应力分别为273.5、260.6和247.5MPa;对应的疲劳循环次数分别为5.87×105、8.87×105和1.4×106。图7为不同载荷下的疲劳寿命分析区域。

由图7可见:下摆臂疲劳寿命最弱(应力最大)的部位为A区，此处定义为高危险区，从寿命最薄弱之处到疲劳寿命满足设计要求的C区，过渡区定义为B区;为更好地比较该结构件的寿命，可分析出A、B、C区的平均寿命和应力之间的关系，见图8。

由图8可见:下摆臂受到的载荷越大，产生的应力越大，相应的疲劳寿命也越低;同时通过分析高危险A区的曲线变化趋势，可以得到下摆臂的高危险区的应力与疲劳寿命之间的关系式为

合格C区的应力与疲劳寿命之间的关系式为

通过分析A、B、C区的平均寿命和应力，得出平均应力分别增加12.9和13.1MPa，疲劳循环次数提高122%，即得出以下结论:下摆臂受到的应力下降10MPa时，疲劳寿命约能提高1倍。

3 仿真和试验对比分析

参考行业和国家相关的试验标准［16-17］，对下摆臂的试验制定了下摆臂总成台架疲劳试验方法。

为能较真实地验证下摆臂所承受的载荷，参考仿真分析的结论，展开相应的台架试验验证。对试验样件的要求是下摆臂外观质量良好，没有损坏;将样件放置在下摆臂疲劳耐久性台架试验的夹具中，如图9所示，其中A处与15kN液压伺服系统相连接，为动力驱动部位;B处为夹具与样件通过紧固件连接，其连接拧紧力矩39N·m;C处为样件通过橡胶衬套与夹具铰接，其转动阻力矩为28N·m;当目视样件能看到裂纹时，则定义为出现了疲劳损坏。分析结果如图9和图10所示。

对于下摆臂在整车道路试验的分析中，具体有:根据整车在各种路面上的载荷，应用六分力测试系统，测试得到作用在汽车车轮中心的6个作用力和力矩，如图11所示。再由多体动力学分析出传递到下摆臂上的作用力和力矩，按照时域载荷，采用疲劳寿命分析程序，可得到其高周疲劳寿命结果。试验时要对整车进行磨合、轮胎气压和四轮定位等状态检测;确定信号的幅值特征和通道间相位关系判断信号是否正确;实际的车轮六分力传感器在数据采集时，应当增加转向角信号，通过后处理对纵向力和横向力进行修正;对于每个雨流循环计算其疲劳损伤，疲劳损伤值根据时间历程来分析;按照选定的损伤累积时间周期，计算每一累积分段的累积损伤值。然后按照损伤要求对各个周期进行取舍。

根据下摆臂的特征，路试选取比利时路、综合路、2号综合路、2号环岛路和S性能路等路面。

由仿真与试验应力和疲劳寿命问的对比表明:疲劳寿命的仿真循环次数为1.4×106，试验循环次数为1×106。仿真对下摆臂的疲劳寿命有所高估。

4 结论

(1)基于多体动力学载荷值、“惯性释放法”结构仿真和疲劳仿真与试验方法，探索出可较好地分析下摆臂疲劳寿命的一体化疲劳寿命分析方法。

(2)研究出应力和疲劳寿命的关系:下摆臂受到的应力下降约10MPa，疲劳寿命约能提高1倍。

(3)在下摆臂的分析和设计过程中，仅应用单一的强度和刚度分析，不能反映该部件在实际行驶过程中承受的载荷，因而不能较好地预测其疲劳寿命;只有进行各种载荷工况下的疲劳寿命分析，才能较全面地满足下摆臂的全寿命设计要求。

［1］Adel Mahmoud Bash，et al.Design Lower Arm Using Optimum Approach［J］.Modern Applied Science，2011，5(1):56.

［2］Bijan Shahidi，et al.System Level Durability Engineering in CAE［C］.SAE Paper 2006-01-1981.

［3］Abdullah S，Kadhim N A，Ariffin A K，et al.Dynamic Analysis of an Automobile Lower Suspension Arm Using Experiment and Numerical Technique，New Trends and Developments in AutomotiveSystem Engineering［M］.Prof.Marcello Chiaberge，ISBN:978-953-307-517-4，InTech，2011.

［4］Abdullah S，et al.A Review on Finite Element Analysis Approaches in Durability Assessment of Automotive Components［J］.Journal of Applied Sciences，2008，8(12):2192-2201.

［5］Al-Asady Nawar A，et al.Comparison Between Experimental Road Data and Finite Element Analysis Data for the Automotive Lower Suspension Arm［J］.European Journal of Scientific Research，2009，29(4):557-571.

［6］成永刚.轿车悬架耐久性试验载荷谱的优化研究［J］.汽车工程，2009，31(5).

［7］Shi Jianpeng.Vehicle Ride Comfort Based on Matching Suspension System［J］.Chinese Journal of Mechanical Engineering，2011，24(2):271-276.

［8］日本汽车技术协会.汽车强度［M］.付嵩元，译.北京:机械工业出版社，1987.

［9］富克斯H O，斯蒂芬斯R I.工程中的金属疲劳［M］.漆平生，徐桂琴，译.北京:中国农业机械出版社，1983.

［10］布洛克B.工程断裂力学基础［M］.王克仁，等译.北京:科学出版社.1980.

［11］Hertzberg Richard W.工程材料的变形与断裂力学［M］.王克仁，等译.北京:机械工业出版社，1982.

［12］Zilincik S，DeFrank J，et al.A New Approach to Evaluating Spot Welds for Automotive Durability［C］.International Body Engineering Conference ＆ Exposition， Detroit，Michigan，United States，1998.9.

［13］Topa M M，et al.Fatigue Failure Prediction of a Rear Axle Housing Prototype by Using Finite Element Analysis［J］.Engineering Failure Analysis，2009(16):1474-1482.

［14］管欣，史建鹏，等.单纵臂式与扭力梁式悬架特征分析［J］.华中科技大学学报(自然科学版)，2011，39(1):86-89.

［15］王弘，等.40Cr钢超高周疲劳性能及疲劳断口分析［J］.中国铁道科学，2003，24(16):93.

［16］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.QCT 513—1999汽车前轴台架疲劳寿命试验方法［S］.北京:中国标准出版社，1999.

［17］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB/T 12443—2007金属材料扭应力疲劳试验方法［S］.北京:中国标准出版社，2007.