完整系统Tzénoff方程的守恒规律

郑世旺

（商丘师范学院 物理与电气信息学院，河南 商丘 476000）

1953年保加利亚科学院院士Tzénoff构造了经典力学系统的一种新型动力学函数称为Tzénoff函数，他建立了一类新型运动微分方程被称为Tzénoff方程。我国学者梅凤翔、程丁龙等把Tzénoff方程推广到了可控力学系统[1]、变质量系统[2]、变质量高阶非完整系统[3]，在专著[4]中又推出了广义Tzénoff函数和广义Tzénoff方程.对称性原理是物理学中更高层次的法则，动力学系统中的守恒量更能揭示深刻的物理规律，动力学系统的对称性与守恒量之间具有一定的内在关系[5]。近年来，对称性与守恒量的研究已经成为力学、物理学、数学等领域的一个非常活跃的课题，且已经取得重要研究成果[6-21]，这些成果大都是借助于动力学系统的Lagrange函数、Hamilton函数和Appell函数来求系统的守恒量，其实在分析力学中有多种运动微分方程，其中最为简捷的是Tzénoff方程，只要给出系统的Tzénoff函数，研究系统的运动规律是比较方便的.目前，Tzénoff方程的对称性与守恒量的研究也有了一些初步成果[22-29]，得到了Tzénoff方程Mei对称性和Mei对称性间接导致的守恒量。研究了完整系统Tzénoff方程的对称性及其守恒规律，给出了导出守恒量的必要条件和守恒量的函数表达式，最后举例说明了研究结果的应用.

1 完整系统的Tzénoff方程

设力学系统的位形由 n个广义坐标 qs（s＝1，…，n）来确定，系统的 Tzénoff函数为[17]：

通过（2）式可求出所有广义加速度：

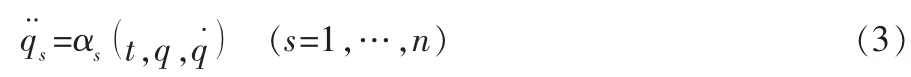
2 Tzénoff方程的Noether对称性及其守恒规律

取时间和坐标的群的无限小变换

Noether对称性是Hamilton作用量在无限小变换下的一种不变性,所以研究Noether对称性必须知道系统的Lagrange函数,而 Tzénoff方程中只给出 Tzénoff函数,所以寻找 Tzénoff方程的Noether对称性及其守恒量，必须将Tzénoff方程变换成Lagrange方程，以找出系统的Lagrange函数。对给定的Tz-énoff函数 K 有：

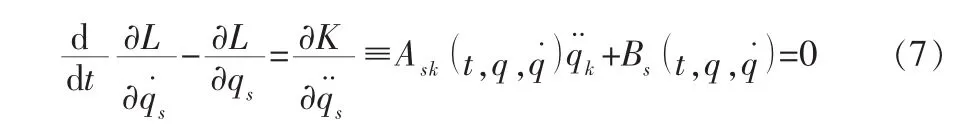
采用文献[6]的方法可求出Tzénoff方程所对应的Lagrange函数

于是有：

定理1：对于Tzénoff方程所对应的Lagrange函数,如果存在规范函数G=G(t,q)使无限小生成元ξ0，ξs，满足恒等式

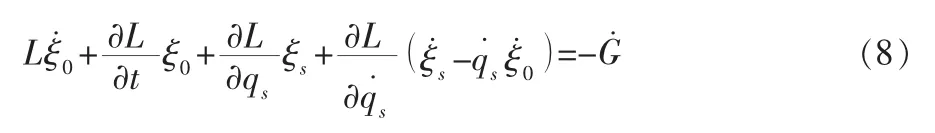
那么Tzénoff方程具有Noether对称性,同时直接导致守恒量：

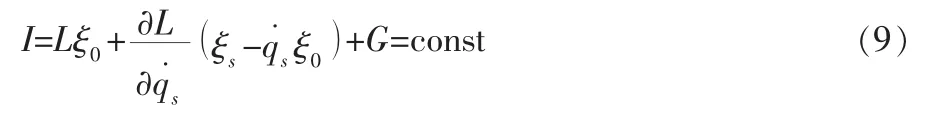
3 Tzénoff方程的Mei对称性及其守恒规律

用变换后的动力学函数代替变换前的动力学函数,若系统运动方程的形式保持不变,则称系统具有Mei对称性。于是有

定义：如果用变换后的Tzénoff函数K*代替变换前的函数K时，方程（2）的形式保持不变，那么这种不变性称为Tzénoff方程的Mei对称性。

根据定义Tzénoff方程的Mei对称性可以写成下列形式：

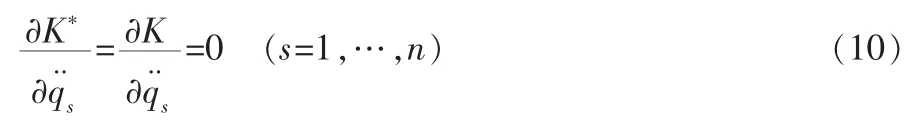
把（6）式代入方程（10）并注意方程（2）有

判据：对于完整力学系统的Tzénoff函数K，若无限小生成元 ξ0，ξs满足方程

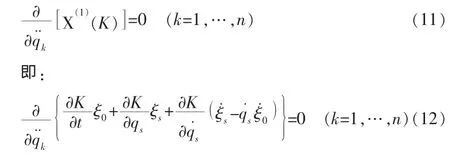
则Tzénoff方程具有Mei对称性。

我国学者对Mei对称性进行了大量研究,一般是借助于动力学系统的Lagrange函数或Hamilton函数来求系统的守恒量。我们企图利用Tzénoff方程和Tzénoff函数通过Mei对称性来寻找一种新的守恒量.

定理2：对于完整力学系统Tzénoff方程Mei对称性的生成元ξ0，ξs，如果能找到规范函数G满足如下结构方程

证明：对（14）式求导并考虑到在Mei对称性情况下判据方程（11）成立，有:

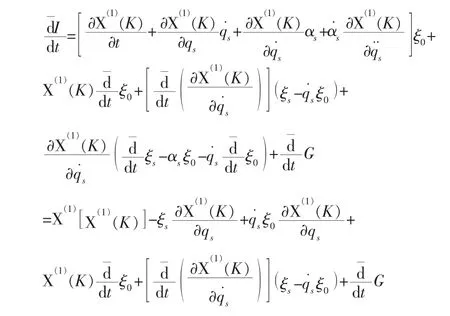
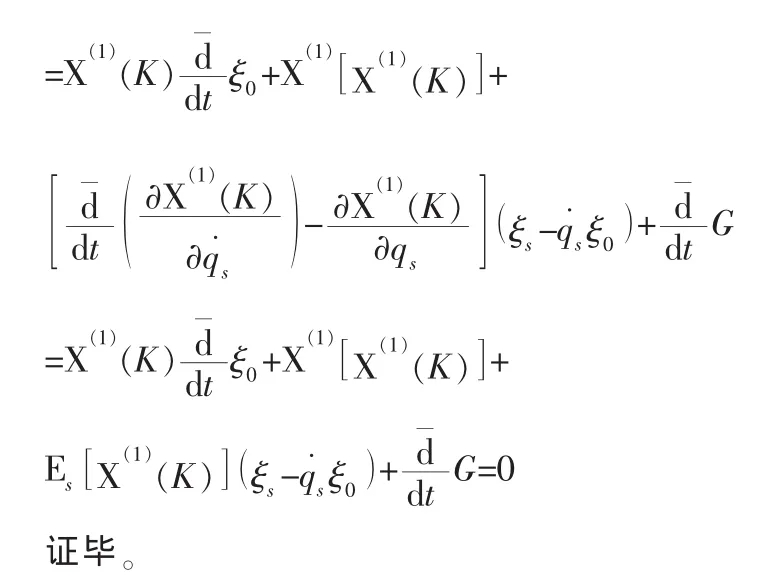
4 应用例子

例：已知完整力学系统的Tzénoff函数为：

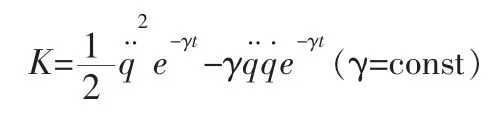
试研究该力学系统的Mei对称性及其所对应的新守恒量。

解：把 Tzénoff函数代入完整力学系统的 Tzénoff方程（2）得：

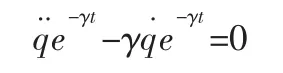
所以该力学系统有关系式：

把 Tzénoff函数代入完整力学系统的 Tzénoff方程Mei对称性的判据方程（12）得：

可找到Mei对称性的生成元

由生成元（17），有 X（1）（K）=0，只能得到平凡守恒量 I=0。由生成元（18）并考虑到（15）式，有：

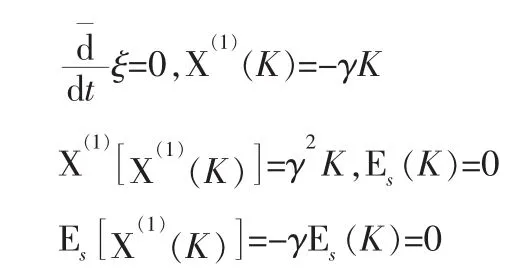
把上面的各关系式代入结构方程（13），又由于该系统有关系式（15），可得到规范函数：

把式（18）和式（19）代入式（14），并注意式（15）可得到系统Tzénoff方程的新守恒量：

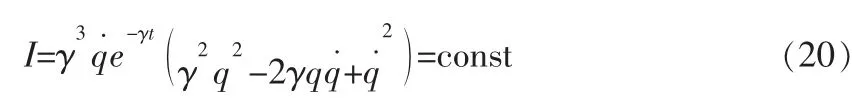
[1]程丁龙.ЦЕНОВ方程对变质量非完整系统的推广[J].北京理工大学学报，1987,3:76-85.

[2]梅凤翔.非完整系统力学基础[M].北京：北京工业学院出版社，1985.

[3]梅风翔.非完整动力学研究[M].北京：北京工业学院出版社，1987.

[4]梅凤翔，刘端，罗勇.高等分析力学[M].北京：北京理工大学出版社，1991.

[5]Noether A E.Invariance Variations problem s[J].Kgl Ges Wiss Nachr G?ttingen Math Phys.1918,Kl,II:235-257.

[6]Mei Fengxiang.Form invariance of Lagrange system[J].Journal of Beijing Institute of Technology,2000,9(2):120-124.

[7]Chen Xiangwei,Liu Cuimei,Li Yanmin.Lie symmetries,perturbation to symmetriesand adiabatic invariants of Poincare equatons[J].Chinese Physics,2006,15(3):470-474.

[8]罗绍凯.Hamilton系统的Mei对称性、Noether对称性和Lie对称性[J].物理学报，2003,52(12):2941-1944.

[9]Chen Xiangwei,Zhao Yonghong and LiYanmin.Conformal invariance and conserved quantities of dynamical system of relative motion[J].Chinese physics B,2009,18(8):3139-3144.

[10]Zhang Yi,MeiFengxiang.Form invariance forsystemsof generalized classical mechanics[J].Chinese Physics,2003,12(10):1058-1062.

[11]梅凤翔.约束力学系统的对称性与守恒量[M].北京：北京理工大学出版社，2004.

[12]楼智美.哈密顿 Ermakov系统的形式不变性[J].2005,54(5):1969-1971.

[13]方建会，丁宁，王鹏.非完整力学系统的Noether-Lie对称性[J].物理学报，2006,55(8):3817-3820.

[14]葛伟宽.一类动力学方程的Mei对称性[J].物理学报，2007,56(1):1-4.

[15]李彦敏.变质量非完整力学系统的共形不变性[J].云南大学学报：自然科学版，2010，32(1):52－57.

[16]贾利群，解银丽，罗绍凯.相对运动动力学系统Appell方程Mei对称性导致的Mei守恒量[J].物理学报，2011,60(4):040201-1-040201-4.

[17]楼智美，梅凤翔.二维各向异性谐振子的第三个独立守恒量及其对称性[J].物理学报，2012,61(11):110201-1～110201-5.

[18]方建会.Lagrange系统Mei对称性直接导致的一种守恒量[J].物理学报，2009,58(6):3617-3619.

[19]孙现亭，韩月林，王肖肖，张美玲，贾利群.完整系统Appell方程Mei对称性的一种新的守恒量[J].物理学报，2012,61(20):200204-1～200204-4.

[20]刘洪伟，李玲飞，杨士通.Kepler方程的共形不变性、Mei对称性与守恒量[J].物理学报，2012，61(20):200202-1～200202-5.

[21]Jiang Wenan,Zhuang Jun,Luo Shaokai.Mei symmetries and Mei conserved quantities for higher-order nonholonomic constraint systems[J].Chinese Physics B,2011,20(3):030202-1～030202-7.

[22]Zheng Shiwang,JIA Liqun,Yu Hong-sheng.Mei Symmetry of Tzénoff Equations of Holonomic System[J].Chinese Physics,2006，15(7):1399-1402。

[23]Zheng Shiwang，Xie Jiafang.,Jia Liqun.Symmetry and conserved quantity of Tzénoff equations for holonomic systems with redundant coordinates[J].Chinese Physics Letters,2006,23(11):2924-2927。

[24]Zheng Shiwang，Xie Jiafang,Jia Liqun.Symmetry and Hojman conserved quantity of Tzénoff equations for unilateral holonomic system[J].Communications in Theoretical Physics,2007,48(1):43-47.

[25]Zheng Shiwang，Xie Jiafang,LiYanmin.Meisymmetryand conserved quantity of Tzénoff equations for nonholonomic systems of non-Chetaev,s type[J].Communications in Theoretical Physics,2008,49(4):851-854.

[26]Zheng Shiwang，Xie Jiafang,Zhang Qinghua.Mei symmetry and new conserved quantity of Tzénoff equations for holonomic systems[J].Chinese Physics Letters,2007,24(8):2164-2166.

[27]Zheng Shiwang，Xie Jiafang，Wang Jian B0，Chen Xiang Wei.Another conserved quantity by Mei symmetry of Tzénoff equation for the non-holonomic systems[J].Chinese Physics Letters,2010,27(3):030307-1-030307-4.

[28]Zheng Shiwang,Wang Jianbo,Chen Xiangwei,Xie Jiafang.Mei symmetry and new conserved quantities of Tzénoff equations for the variable mass higher-order nonholonomic system [J].Chinese Physics Letters,2012,29(2):020201-1～020201-4.

[29]郑世旺，王建波，陈向炜，李彦敏，解加芳.变质量非完整系统Tzénoff方程的Lie对称性与其导出的守恒量[J].物理学报，2012,61(11):111101-1～111101-5.