基于MATLAB和Pro／E的四杆机构多目标优化设计＊

吴义成，吴玉国

（1.马鞍山职业技术学院，安徽 马鞍山 243000；2.安徽工业大学机械工程学院，安徽 马鞍山 243000）

0 前言

机械优化是数学规划理论、机械结构分析理论以及计算机应用技术等多学科交叉形成的综合决策学科［1］。机械机构中，四杆机构使用广泛，无论是在日常生产生活还是军事领域当中都被大量应用，如起重机、汽车转向机构、飞机起落架机构及雷达天线俯仰机构等［2］。根据机械的用途和性能要求的不同，四杆机构的设计要求基本上可归纳为：满足预定的运动规律要求、满足预定的连杆位置要求以及满足预定的轨迹和性能要求。常用的设计方法有解析法、作图法和实验法。这些常规的设计方法在针对单个设计目标时，一般具有很好的效果。但在实际应用中，往往是多个设计目标同时出现，而且经常会出现各目标之间互相矛盾和制约的问题，此时，常规设计方法可能会失效。本文以四杆机构中的曲柄摇杆机构为例，针对一个实际应用过程中多个优化目标的实现，建立了相应的数学模型，使用MATLAB 优化工具箱，对具有多个目标函数的数学模型进行求解，讨论了在特定条件下，各组不同解的优劣性和满足设计要求的取舍问题；并使用Pro／E 机构运动仿真模块对该求解结果进行验证。此综合方法为四杆机构的多目标优化设计问题提供了一个很好的解决途径。

1 问题提出及数学模型的建立

曲柄摇杆机构是铰链四杆机构中的一种，在实际工程应用中，该型机构应用广泛，如缝纫机踏板机构、搅拌器机构等［3］。要求设计一曲柄摇杆机构，能同时实现以下几个要素［4］：

（1）为提高机构的急回性能，极位夹角θ尽可能大（0°＜θ≤17°）；

（2）为改善机构的传力性能，当该机构曲柄与连杆重叠共线时，最大压力角αmax尽可能小（0°＜αmax≤55°）；

（3）该摇杆摆角Δψ＝60°。

1.1 设计变量的确定

为更好地求解，现直观地表示出该曲柄摇杆机构的结构参数示意图，如下图1所示：

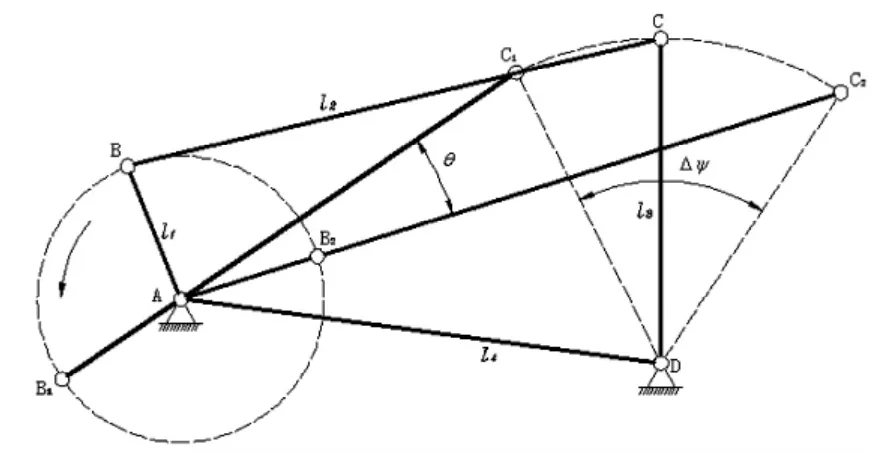
图1 曲柄摇杆机构示意图［3］

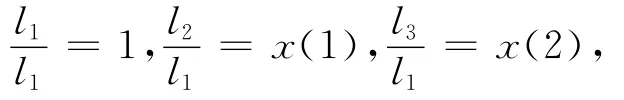
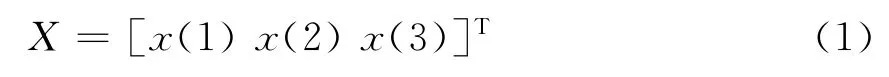
1.2 目标函数的建立

当曲柄摇杆机构的各杆长值确定后，该机构的摇杆摆角、最大压力角及极位夹角都会确定下来，即该机构的各项性能也能确定下来。这里，将摇杆摆角Δψ＝60°这个目标处理为无限接近60°这个目标值，定义为一目标函数，求之同60°之差的绝对值的最小值。由上图1及设计要求，可列出该设计的分目标函数分别为：

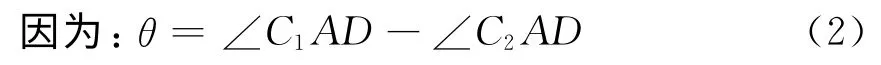
由余弦定理，所以有：

这里，根据设计要求，极位夹角θ尽可能大为好。为了能实现用MATLAB编程求解，做一下处理，定义f1（x）＝－｜θ｜。这样就实现了f1（x），f2（x），f3（x）→min，满足MATLAB 优化工具箱对目标函数的统一要求。对各目标函数的范围做进一步明确：

1）为保证极位夹角尽可能大，确定极位夹角不小于10°，即10°≤θ≤17°，于是转换成弧度，有：

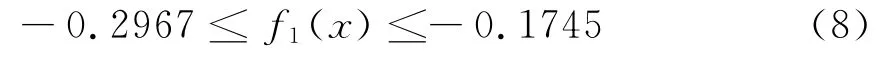
2）由设计要素的条件得：

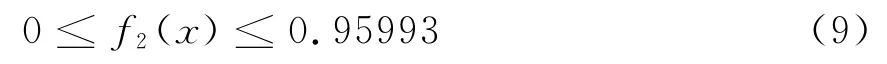
3）为保证摇杆的摆角Δψ尽可能接近60°，使－1°≤f3（x）≤1°，转换成弧度，有：

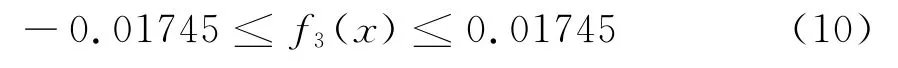
1.3 约束条件的确定

曲柄摇杆机构要满足曲柄存在的条件。其中最长杆与最短杆的长度之和≤其他两杆长度之和；四杆中要有一个为最短杆。取l1＝1，因此有：

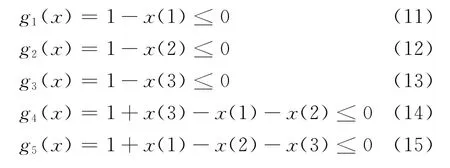
2 使用MATLAB 优化工具箱进行优化求解

MATLAB的优化工具箱选用最佳方法来求解，初始参数输入简单，语法特征符合数学表达式的书写，编程工作量大大减少，有着很大的优越性［5］。该优化工具箱提供了一般和大型的非线性优化函数，同时还提供了线性规划、二次规划、非线性方程求解的工具。本例属于一般非线性多目标规划问题，其标准型为：

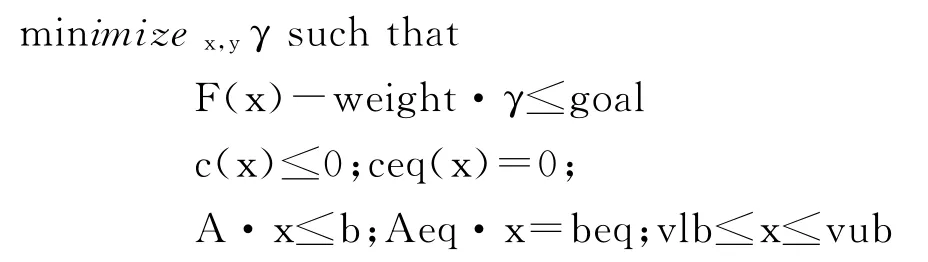
调用MATLAB优化工具箱中非线性规划求解函数fgoalattain［6］来求解。其命令的基本格式：［X，fval，attainfactor，exitflag］＝fgoalattain（＠ObjFun，x0，goal，weight，A，B，Aeq，Beq，vlb，vub）；其中各个参数的含义如下：ObjFun 为定义求解的多目标函数；x0为变量初值；A，B为约束函数中线性不等式约束的参数；Aeq，beq为约束函数中线性等式约束的参数；c（x），ceq（x）均为非线性函数组成的向量；vlb，vub分别是变量X 的下限和上限值；goal是目标函数边界组成的向量；Weight是目标函数的权重值［7］。对于判断求解是否有效可通过attainfactor和exitflag 两个参数来确定：当exitflag＞0时，表示所求的解收敛；当attainfactor＞0时，表示目标值没有溢出goal。对于本例中求解最优解，分两个步骤进行：

1）根据前文叙述的目标函数表示法，建立M文件ObjFun.m，定义各个目标函数：

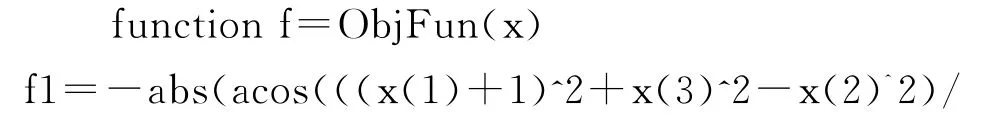
2）根据非线性多目标规划求解函数fgoalattain的形式，建立主程序qiujie.m 函数：

3 使用Pro／E软件仿真功能对多目标优化结果进行验证

针对多目标优化设计，由于含有多个目标值，各个目标之间往往存在互相制约和矛盾的情况，而且各个目标函数的权重值不好确定，因此非线性多目标优化结果往往很难准确给出最优结果。在使用MATLAB优化工具箱求解时，只有在明确了各个目标函数的权重值时，才有可能。此四杆机构的优化设计含有三个目标函数，在满足不同的目标函数权重值前提下，理论上满足条件的解应该是无穷多个。现在令各目标函数权重值weight＝0.3333，即在各目标函数同等重要的情况下，在不同杆长度段初始值运行程序进行搜索，得出满足该设计目标的优化值，现取杆长初值x0 ＝［2 2 2］～［6 6 6］时，各组解的情况，列表如下：

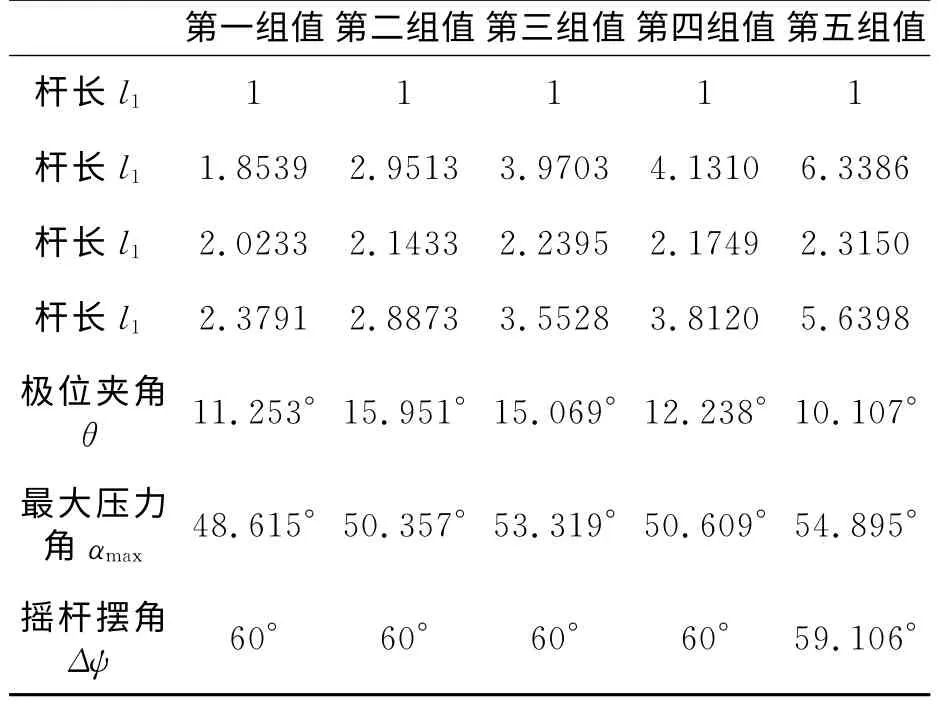
表1 相同目标函数比重值时的优化结果

由上表数据可以看出，满足该多目标优化解的结果很多，通过表中数据可以确定第二组解是相对最 优解，其 中：l1＝1，l2＝2.9513，l3＝2.1433，l4＝2.8873。

仿真的重要工具是计算机和仿真软件，Pro／E操作软件是美国参数技术公司（PTC）旗下CAD／CAM／CAE一体化的三维软件［8］。将以上所求的曲柄、连接杆、摇杆和固定杆长值都扩大100倍，在Pro／E软件中进行尺寸设计、装配并设置连接后，添加驱动器伺服电动机，进行运动仿真，当曲柄与连架杆运动到重叠共线时，仿真状态位置图如下图所示：

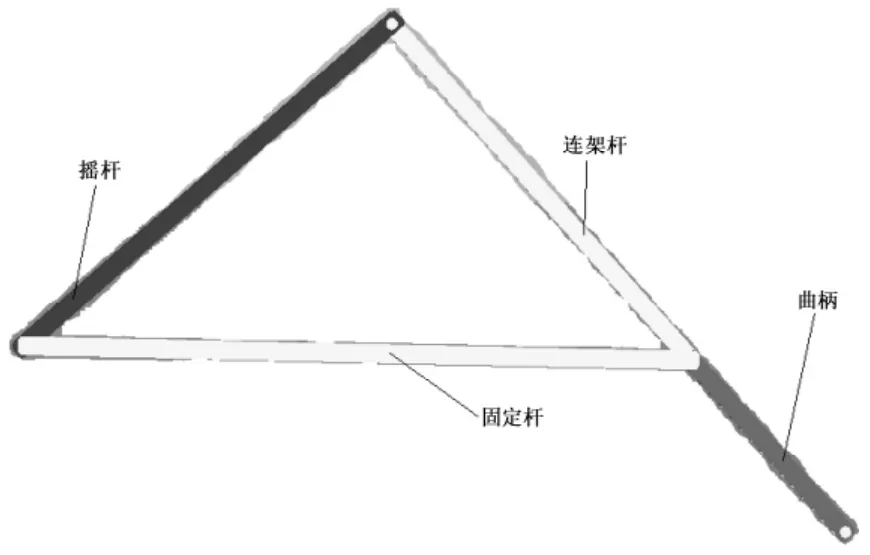
图2 四杆机构运动仿真位置图

经过Pro／E 软件运动仿真，该组结构参数完全满足此多目标优化设计的要求，摇杆摆角为60°，极位夹角相对最优，最大压力角也满足要求。

4 结语

在进行四杆机构及其他类型机构的多目标优化设计时，对于各个目标函数做统一边界处理，明确各目标函数在整个数学模型中的权重值和所要设计的机械性能特性，应用多目标优化设计的线性加权法［9］，使用MATLAB 优化工具箱，进行程序编制，找出满足条件的解，再进行性能相对比较分析，寻找到比较适合各设计目标的最优解，最终通过Pro／E软件进行运动仿真，将在MATLAB软件中求解的数据导入到Pro／E 软件中，对结果进行验证。该方法具有方便、快捷、高效和准确的特点，为较好地解决四杆机构多目标优化设计问题提供了一个途径。

［1］包家汉，裴令明，谢能刚，等.机构多目标优化与博弈决策设计［J］.安徽工业大学学报（自然科学版），2005，（4）：108－111.

［2］林宗良.机械设计基础［M］.北京：人民邮电出版社，2009，（4）：105－115.

［3］吴义成.曲柄摇杆机构再现已知运动规律的优化求解［J］.装备制造技术，2011，（10）：42－44.

［4］孙靖民，梁迎春.机械优化设计［M］.北京：机械工业出版社，2006.

［5］席平原.应用MATLAB工具箱实现机械优化设计［J］.机械设计与研究，2003，（6）：40－42.

［6］蔡旭晖，刘卫国，蔡立燕.MATLAB 基础与应用教程［M］.北京：人民邮电出版社，2009.

［7］覃金彩，史彬华，江全才.基于Matlab的V 带传动多目标优化设计［J］.三峡大学学报（自然科学版），2011，33（3）：101－102.

［8］周晓平，张云莉，朱双霞.基于Pro／E的搅拌器参数化运动仿真设计［J］.煤矿机械，2012，（3）：255－256.

［9］朱延飞，王刚，姚养无.平面组合连杆机构的多目标优化设计及仿真［J］.火炮发射与控制学报，2008，（12）：94－96.