基于ANSYS的曲柄摇杆机构的仿真分析及优化设计
赵浩东
(山东交通学院,济南 250300)
0 引言
近年来,我国经济技术快速发展,各种机械设备对传动结构的性能要求也越来越高。在机械设计及其制造行业内,曲柄摇杆机构的应用场景十分广泛,是一种较为经典的机械传动形式,能够实现多种复杂轨迹的运动目标,也可以使其具有和不具有急回特性。曲柄摇杆具体尺寸和参数的设计需要以特定的运动轨迹作为依据[1-3]。在实际的设计过程中,往往是根据数量有限的几个点作为运动轨迹的参考点,不能完全使曲柄摇杆机构和预期的轨迹相吻合,这就需要通过更为精准的参数作为设计依据,不断优化曲柄摇杆的结构形式[4]。曲柄摇杆机构的运动副具有较大的接触面积,可以承载较大的力,并且还具有润滑性能好、磨损现象较轻、稳定性强等优点。曲柄摇杆机构结构优化的最重要的目标就是在保证力学性能和使用功能的基础之上,还可以具有重量轻、结构紧凑、传动效率高等特点[5-7]。牛头刨床、设备输运机、石头破碎机、雷达调整结构中,都有曲柄摇杆机构的应用,本文主要选择曲柄摇杆机构在雷达调整机构中的应用为例,对其进行有限元仿真分析。
1 曲柄摇杆在雷达调整机构中的应用特点
一般情况下,曲柄摇杆机构能够使雷达实现升降和调平的功能,与雷达进行接触的为摇杆,动力杆为曲柄,当曲柄转动时,可以使摇杆发生0~90°的转动,从而调整雷达的角度[8-9]。车载式雷达一般安装在车厢上,天线必须充分裸露在外部环境内,为了能够及时接收信号的方位,必须能够自动精准控制雷达的角度和方向,而曲柄摇杆机构的结构特点正好能够满足这一要求。调整结构的材料,选择质量较轻的铝合金,在雷达自身的重量及风速较大时,结构的材料也会采用钢等力学性能较好的金属材料[10]。雷达调整机构的传统设计思路是采用刚性的机械结构,其自身结构支腿之间的位置关系是固定的。在实际使用过程中,大型雷达对其调整结构的刚度要求非常高,需要足够的板壳厚度和摇杆截面积,但是厚度和截面积的增加又与减轻重量、缩小结构的目标相矛盾,因此,要在保证雷达调整结构各方面性能都能满足使用需求的基础上,对其厚度和摇杆的截面积进行优化。
2 曲柄摇杆机构强度的计算
在低速重载的曲柄摇杆机构传动中,曲柄摇杆的静强度具有十分重要地位,因此对其强度进行计算是很有必要的。通常v<0.6 m/s的转动速度视为低速转动。假若低速曲柄摇杆的移动也按额定功率选择和计算,其经济性较差,不利于成本的节约。额定功率曲线上各点相对应的条件性安全系数n>8~20,较静强度安全系数会明显增大很多。除此之外,当对曲柄摇杆机构进行有限寿命计算时,若其机械设备本身要求的使用寿命相对较短的情况下,并且其使用功率过高,则曲柄摇杆机构的的静强度验算也是必不可少的。曲柄摇杆机构的强度验算公式如式(1)。
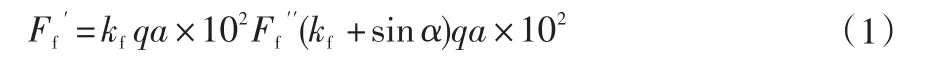
式中:a为曲柄长度,单位为mm;q为重力载荷,单位为kgf/m;分别为重力在摇杆上的作用力和反作用力,单位为N。
曲柄摇杆机构的的静强度计算公式如式(2)。

式中:n为静强度安全系数;Q为摇杆极限拉身载荷,单位为N;KA为工况系数;F为有效拉力,即有效圆周力,单位为N;Fc为离心力引起的拉力,单位为N,其计算式为Fc=qv2;q为曲柄摇杆机构的质量为kg/m;v为转动速度,单位为m/s;当v<4 m/s时,Fc可忽略不计;Ff为悬垂拉力,单位为N,在中选择大者;[n]为许用安全系数,一般为4~8;如果按最大尖载荷峰Fmax来代替KAF进行计算,则可为3~6;对于速度较低,从动系统惯性较小,不太重要的传动或作用力的确定比较准确时,[n]可取较小值。
由以上公式并结合《机械设计手册》的相关数值可以得到Q=30.1×103,KA=1.4,由前面算得F=10 kN,q=5.6 kg/m,由前面计算知 v=0.248 m/s<4 m/s,故Fc可忽略不计;取 α=90°,则 F′=F″=0,故 n2.22,则[n] 在2~8之间。
故曲柄摇杆机构的强度安全。
3 曲柄摇杆机构中摇杆的有限元仿真分析及优化
3.1 三维模型的建立及网格的划分
雷达接受信号的强度和质量会受到其自身角度的影响,因此必须保证雷达可以较为精准地进行角度的调整,同时也会要求曲柄摇杆机构的运行必须具有较强的可靠性和精密性。摇杆和雷达直接接触,会受到雷达重力和风力的影响而发生应力集中和变形的影响,因此,在对曲柄摇杆设计的过程中,必须要注意各组成部分的应力集中和变形的影响[11]。由于摇杆件和雷达直接接触,其发生应力集中和变形的可能性更高,因此本文主要以曲柄摇杆机构中的摇杆件为例,对其进行有限元仿真分析,采用Solid⁃Works软件绘制了摇杆的三维模型,忽略了对仿真分析没有影响的倒角等特征,其三维模型图如图1所示。
由于雷达调整机构使用的摇杆结构相对较为规则,因此本文利用ANSYS模块中的Mesh网格划分工具,采用结构化网格进行划分。网格划分完成后得到网格数为76 826,网格划分图如图2所示。
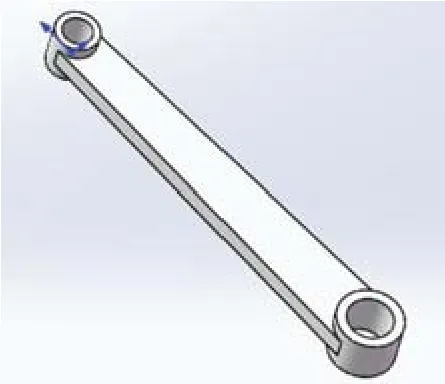
图1 摇杆的三维模型图

图2 网格划分图
3.2 边界条件设置及仿真求解
本文将SolidWorks中建立的摇杆的三维模型,导入到在有限元仿真软件ANSYS中进行求解计算,摇杆的材料为钢,考虑到雷达信号结构设备的最大重量和最大风力作为极限工况进行分析,最大载荷为2 000 N,受力面为摇杆与雷达的接触面,即摇杆的上表面,固定约束为2个接触孔,摇杆的转动方向为自由约束[12]。摇杆的应力分布云图如图3所示,摇杆的变形分布云图如图4所示。

图3 摇杆应力分布云图
由图3可知,摇杆的最大应力为168.71 MPa,最大应力分布在上接触孔与雷达接触的位置,最小应力分布在下接触孔与支腿接触的位置。最大应力小于屈服极限,尽管能够满足力学的性能要求,但是应力集中现象仍较为明显,应对超大载荷的能力相对较弱。
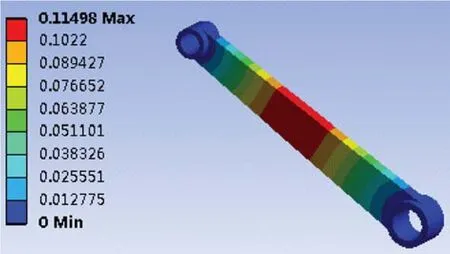
图4 摇杆的变形分布云图
由图4可知,摇杆的最大变形发生在摇杆的中间部位,最大变形量为0.11 mm;最小变形发生在摇杆的两端,变形量相对较小,但是仍然存在一定的变形,不利于雷达角度的精确控制[13]。
3.3 摇杆结构优化后的求解结果
根据图3和图4的仿真结果,对摇杆应力集中较为明显的上接触孔与雷达接触区域进行加厚,整体的摇杆的厚度也增加了2 mm,应力集中较小的下接触孔进行了减厚,去除了部分材料,结构优化后摇杆的应力分布云图如图5所示,摇杆的变形分布云图如图6所示。
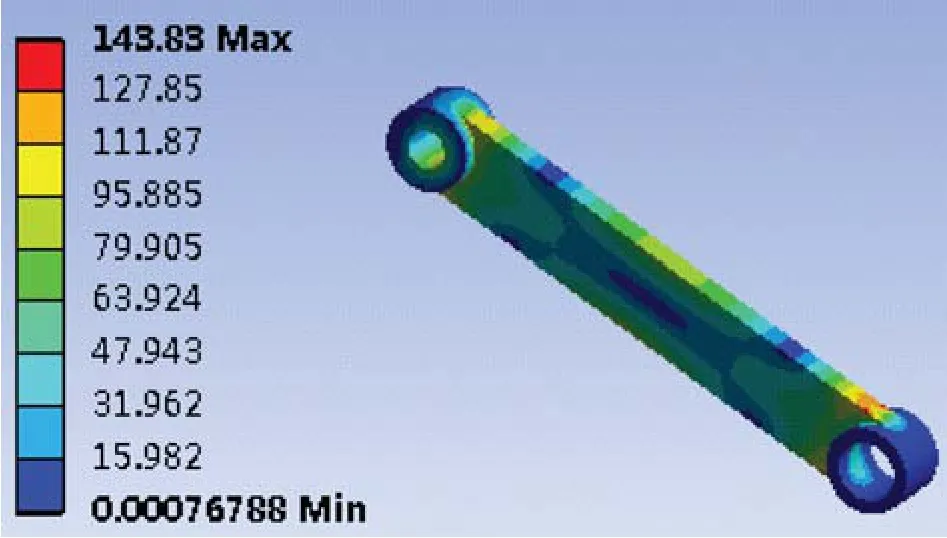
图5 优化后摇杆的应力分布云图
由图5可知,结构优化后摇杆的最大应力为143.83 MPa,最大应力分布在两端上表面,最小应力分布在下接触孔与支腿接触的位置。最大应力与优化前相比明显降低,应对超大载荷的能力增强。

图6 优化后摇杆的变形分布云图
由图6可知,优化后摇杆的最大变形仍然发生在摇杆的中间部位,最大变形量为0.05 mm;最小变形发生在摇杆的两端,变形量与优化前相比明显降低,有利于雷达角度的精确控制。
4 结束语
综上所述,曲柄摇杆是机械设备中较为常见的传动机构,在雷达调整结构等领域有着重要的应用。在进行曲柄摇杆设计的过程中,要选择合适的材料,并对其结构进行不断地优化和改善,尽量避免应力集中和变形较大的现象出现,保障机械设备能够持续可靠运转。

