基于功率谱估计的伺服系统机械谐振分析

朱琰虹，文光武

（1广州数控设备有限公司，广州 510530；2广州数控信息科技有限公司，广州 510603）

0 引言

机械谐振是伺服系统中十分常见的一种现象。伺服系统的机械传动部分经常使用传动轴、变速器、联轴器等传动装置连接电机和负载，而实际传动装置并不是理想刚体，存在一定的弹性，通常会在系统中引发机械谐振[1]。当控制系统输入的激励力的强迫振荡频率接近机械系统的自然谐振频率时，会导致机械系统在共振频率附近产生剧烈震荡。实际机械系统中柔性耦合因素的改变会改变系统的稳定裕度、增加系统的控制难度，甚至会使系统不再稳定，造成装置剧烈震动，导致机械结构受到冲击和变形，极易发生破坏性事故[2]。现代伺服技术中通常对电机转速或转子电流进行高速采样，再利用傅里叶变换求得信号的幅度谱和相位谱来分析机械谐振[3]。本文考虑到机械谐振产生的随机性，所采样信号是确定性信号和随机信号的叠加，而随机信号是无始无终的并具有无限能量，不满足绝对可积的条件[4]，因此可以通过研究其功率在频域上的分布，即功率谱密度或功率谱，从而实现对伺服系统机械谐振的分析。

1 随机信号

随机信号可分为平稳随机信号和非平稳随机信号。各态历经信号是指无限个样本在某时刻所历经的状态，等同于某个样本在无限时间里所经历的状态的广义平稳随机信号[5]。现实的随机信号为大部分可逼近各态历经的平稳随机信号，在各态历经情况下，离散随机信号下的集合平均等于时间平均。随机信号不能用确定性的时间函数来描述，只能用统计的方法研究，其统计特性通常用均值、方差、相关函数与协相关函数来表征。

离散随机信号x(n)的自相关函数如式（1）。

两离散随机信号 x(n)和y(n)之间的互相关函数如式（2）。

除去均值后随机信号x(n)的相关性用自协方差函数如式（3）。

两离散随机信号x(n)和y(n)之间的协方差用互协方差函数来描述，如式（4）。

式（1）、式（2）、式（3）、式（4）中：n和m分别为随机信号的不同时刻；E(x)为随机信号的数学期望。

自相关函数或自协方差函数可用来检测混有随机噪声的信号，1个系统可以通过系统输入和输出信号序列间的互相关函数最大值出现的位置来确定延迟。

2 功率谱

2.1 功率谱密度

功率谱表示随机信号频域的统计特性，有明显的物理意义，1个信号的功率谱密度是其自相关函数的傅里叶变换[6]。

离散随机信号的功率谱密度表示如式（5）。

两离散随机信号互相关函数的傅里叶变换定义为互功率谱密度函数如式（6）。

式（5）、式（6）中：m为随机信号的时刻；ω为数字域频率。

2.2 功率谱估计

各态历经随机信号的集合平均等于时间平均，因此从任何一个样本即可得出随机信号的全部信息。根据时间序列的一个有限观察x(n)，(n=0，1，…，n-1)来估计功率谱密度，称为功率谱估计。功率谱估计通常采用直接法和间接法2种方法[7]，直接法又称周期图法，它是把随机序列x(n)的N个观测数据视为1个能量有限的序列，直接计算x(n)的离散傅里叶变换x(k)，然和再取其幅值的平方，并除以N。

用直接法的功率谱估计，当数据长度太大时，谱曲线起伏加剧，若N太小，谱的分辨率不好，Bartlett法和Welch法是2种改进的直接法。

Bartlett法是将N点有限长序列x(n)分段求周期图再平均。

Matlab代码：

clear；

Fs=1000；

n=0:1/Fs:1；

xn=cos（2*pi*40*n） +3*cos（2*pi*100*n） +randn（size（n））；

nfft=1024；

window=boxcar（length（n））；

noverlap=0；

p=0.9；

[Pxx，Pxxc]=psd （xn，nfft，Fs，window，noverlap，p）；

index=0:roud（nfft/2-1）；

plot_Pxx=10*log10（Pxx（index+1））；

plot_Pxxc=10*log10（Pxx（index+1））；

Welch法对Bartlett法进行了2个方面的修正，一是选择适当的窗函数，二是在分段时使各段之间有重叠。

Matlab代码：

clear；

Fs=1000；

n=0:1/Fs:1；

xn=cos（2*pi*40*n） +3*cos（2*pi*100*n） +randn（size（n））；

nfft=1024；

window=boxcar（100）；

window1=hamming（100）；

window2=blackman（100）；

noverlap=20；

range='half'；

[Pxx，f]=pwelch （xn， window， noverlap，nfft，Fs，range）；

[Pxx1，f]=pwelch （xn，window1，noverlap，nfft，Fs，range）；

[Pxx2，f]=pwelch （xn，window2，noverlap，nfft，Fs，range）；

plot_Pxx=10*log10（Pxx）；

plot_Pxx1=10*log10（Pxx1）；

plot_Pxx2=10*log10（Pxx2）；

随机信号通过离散时间线性非时变系统

当广义平稳随机序列x(n)输入到离散时间线性非时变系统时，系统输出y(n)与系统的单位取样响应h(n)存在关系如式（7）。

线性非时变系统输入和输出的互相关如式（8）。

式（7）、式（8）中，n和k分别为随机信号的不同时刻。由此可知，输入和输出间的互相关函数是单位取样响应的共轭序列和输入自相关序列的卷积，两边取傅里叶变换如式（9）。

显而易见，由自功率谱和互功率谱的测量可确定系统的频率特性如式（10）。

式（9）、式（10）中，ω为数字域频率。

3 功率谱估计在机械谐振分析算法中的应用实现

目前，功率谱估计已经应用在广州数控设备有限公司某伺服驱动的机械谐振分析算法中。数控机床进给传动系统的单轴驱动控制示意如图1所示。

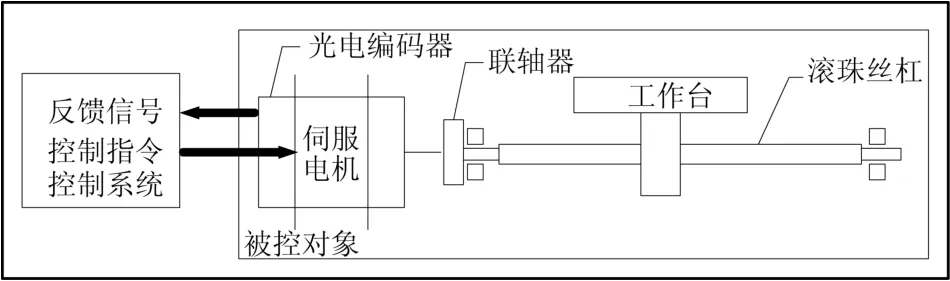
图1 单轴控制示意图

图中，输入信号是控制系统产生的转矩指令（电压或电流模拟量信号），激励力由永磁同步电机产生。由联轴器、工作平台、滚珠丝杠副组成的机械传动环节等效为1个双惯量旋转系统，该系统的输入为电机扭矩与负载扭矩，输出为电机角速度与负载角速度。电机和负载端的转动惯量以及轴的刚度使双惯量旋转系统产生谐振频率点（torsional natural frequency，TNF）和反谐振频率点（anti-resonance frequency，ARF）[8]，当系统激励力的频率接近特定频率时就引起机械谐振。因为系统的频率特性可以通过自功率谱和互功率谱来确定，本文采用对系统进行持续地激励来获取系统在激励过程中的输入和输出数据，并对输入和输出数据做功率谱估计，从而得到系统的频率响应。

图2所示为双惯量旋转系统典型的伯德图（Bode diagram）。

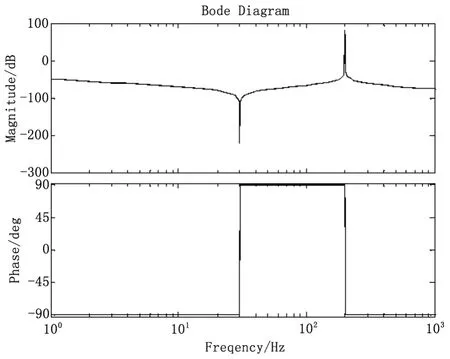
图2 双惯量旋转系统的伯德图

3.1 激励信号

本文提出的系统频率特性测试采用扫频法进行激励。扫频法是以频率在待测频率范围内连续平稳变化的等幅值的正弦信号作为激励源的测试方式，常用的扫频信号有白噪声信号和Chirp信号。在实际应用中，一般采用伪随机二进制序列（Pseudo-Random Binary Sequence，PRBS）代替白噪声信号，PRBS是1种伪随机的二位式周期序列，它的输出结果只有2种电平，同时，在单个周期内数值可以看作是随机变化的。常用的PRBS有M序列（最长线性反馈移位寄存器序列）、L序列（逆重复M序列）等[9]，M序列信号如图3所示。

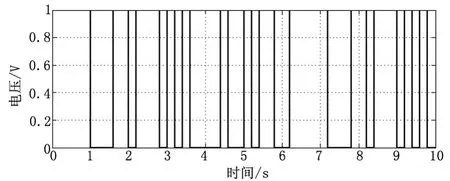
图3 M序列信号波形

Chirp信号是调频脉冲扫频信号是雷达和通信领域经常使用的信号[10]，在频率特性测试中，用到的是Chirp信号的实部，如式（11）。

式中：A为扫频幅值； β为频率变化速率； f0为起始频率。Chirp信号基于余弦函数的变化规律，且瞬时频率随时间发生线性变化。通常，扫频测试关注的频率段是0～1 000 Hz，以驱动单元的伺服周期为61.25μs为例，在实际采样中采样频率取8 kHz绝对满足香农定理。

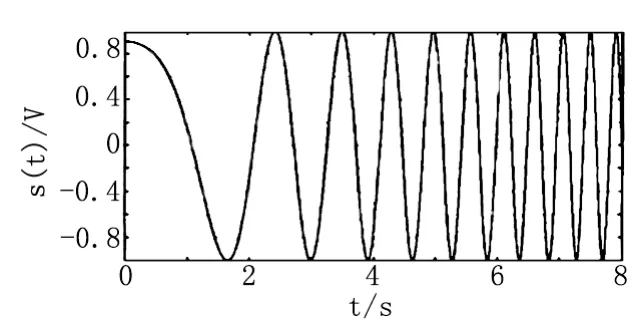
图4 Chirp信号波形

扫频信号在驱动单元的嵌入式芯片中实现，TMS320F28377是一款TI高性能TMS320C28x系列32位浮点单/双核DSP处理器，它可以轻松通过多级移位寄存器的线性反馈产生M序列，也可以快速处理余弦和平方运算产生Chirp信号。

3.2 采样数据分析

在分析扫频信号时，输入数据取转矩指令信号，输出数据取速度反馈信号。由式（10）可知，线性非时变系统的频率特性可以通过自功率谱、互功率谱来确定，式（10）中的Sxx(ejω)是输入转矩信号的自功率谱密度函数，Syx(ejω)是速度反馈信号和输入转矩信号的互功率谱密度函数。

用C语言实现功率谱密度的计算：

intnfft；

if（winlength%2==1） winlength-=-1；

nfft=winlength；

intistart=0，step，iter，i，j；

double scale=0；

CComplexX_tmp；

CComplexY_tmp；

double*window= （double*）malloc（sizeof（dou⁃ble）*winlength）；

double*X_re= （double*） malloc（sizeof（dou⁃ble）*winlength）；

double*X_im= （double*） malloc（sizeof（dou⁃ble）*winlength）；

double*Y_re= （double*） malloc（sizeof（dou⁃ble）*winlength）；

double*Y_im= （double*） malloc（sizeof（dou⁃ble）*winlength）；

CComplex*cpsd= （CComplex*） malloc（sizeof（structCComplex_t） * （nfft/2+1））；

step=winlength-noverlap；

iter=1+（datalength-winlength）/step；

for （i=0；i＜winlength；i++）

{

window[i]=0.54-0.46*cos（2*PI*i/（win⁃length-1））；

scale+=window[i]*window[i]；

}

scale=scale*iter*fs；

for （i=0；i＜=nfft/2；i++）

{

cpsd[i].re=0.0；

cpsd[i].im=0.0；

}

for （i=0；i＜iter；i++）

{

f

or （j=0；j＜winlength；j++）

{

X_re[j]=x[j+istart]*window[j]；

Y_re[j]=y[j+istart]*window[j]；

X_im[j]=0.0；//虚部为0

Y_im[j]=0.0；//虚部为0

}

if （!Fft_transform （X_re， X_im， win⁃length）） exit（1）；

if （!Fft_transform （Y_re， Y_im， win⁃length）） exit（1）；

for （j=0；j＜=nfft/2；j++）

{

X_tmp.re=X_re[j]；

X_tmp.im=X_im[j]；

Y_tmp.re=Y_re[j]；

Y_tmp.im=Y_im[j]；

cpsd[j] =add （cpsd[j]， multiply（X_tmp，myconj（Y_tmp）））；

}

istart=istart+step；

}

for （i=0；i＜=nfft/2；i++）

{

cpsd[i]=multiplybynum（cpsd[i]，2.0/scale）；

}

cpsd[0]=multiplybynum（cpsd[0]，0.5）；

cpsd[nfft/2]=multiplybynum （cpsd[nfft/2]， 0.5）；

free（window）；

free（X_re）；

free（X_im）；

free（Y_re）；

free（Y_im）；

在C程序中实现计算转矩指令信号的自功率谱密度以及速度反馈信号和转矩指令信号之间的互功率谱密度，再通过式（10）计算出H(ejω)，并进一步计算出系统伯德图的幅值和相位，如式（12）。

式中：H为系统的频率特性函数，由此可以确定系统的反谐振频率点和谐振频率点。

3.3 扫频测试结果

系统激励采用Chirp信号，扫频时间设置为10 s，初始频率为1 Hz，终止频率为1 kHz，采样频率为8 kHz。转速由反馈的电机转角位置计算而得，负载惯量盘的数量依次为：0、1、2、3、4、5。激励信号的幅值依次为：500、712、935、1 024（该数值是模数转化器电流输入的数字量，其中1 024对应的电流值为电机额定转矩6 A）。对每一种工况均重复4次扫频测试，分析不同的负载惯量和扫频幅值下系统的频率特性差异。表1是分析每次的测试数据得到的谐振点位置信息，表2是分析每次的测试数据得到的反谐振点位置信息，每种工况重复测试4次。

观察表1和表2的数据可以看出：系统谐振频率随负载的增加而变小，并且在相同工况下重复4次测试得到的系统谐振频率点的一致性很好。

4 结束语

本文提出把数字信号处理中的功率谱估计运用在伺服系统的机械谐振分析中，依据各态历经情况下离散随机信号的集合平均等于时间平均的特性，通过功率谱估计算法分析系统的频率响应更具有实验价值。实验结果表明：计算出来的反谐振频率和谐振频率反映了系统的频率特性，为伺服单元速度环和位置环闭环带宽的配置提供了依据，具有较好的工程应用价值和可行性。

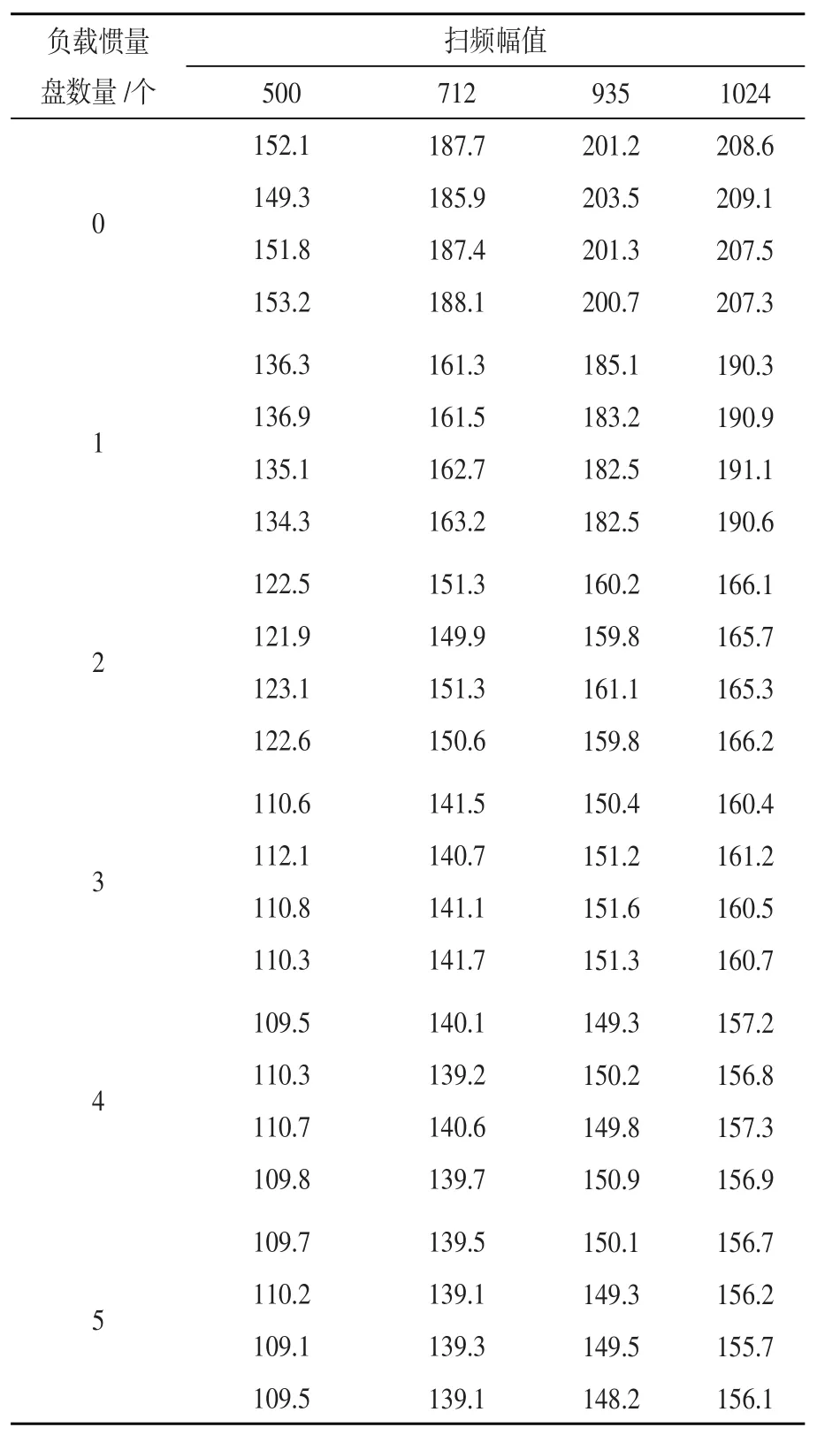
表1 系统谐振频率点

表2 系统反谐振频率点