基于程序分析和0-1整数规划模型的1号车间生产线平衡改善设计*
郭继东,张开彬,江俊豪,梁钰艳,冯彩萍,周大为
(北京理工大学珠海学院工业自动化学院,广东珠海 519088)
0 引言
随着市场经济体制改革的不断深入,中国实木家具产业得到了快速发展,已从传统的手工业发展成为具备相当规模的现代工业化产业。而家具加工制造企业现代工业化产业的重点在于生产线问题的研究。在针对于国内外家具加工制造企业的所有生产线问题的研究中,主要问题有生产线的平衡率、生产线节拍、瓶颈工序、生产线的生产布局等。这些问题严重地影响着生产线的平衡,阻碍了企业生产线效率的提高和生产成本的降低,而最终使企业在竞争中处于劣势[1]。
为了让企业能够获得更大的利润,并且在市场竞争中取得一席之地,生产线优化改善是每个企业的兵家必争之地。但是目前国内家具企业多以“人海战术”的生产模式,甚至并无生产线的概念,所以引入一套简明易懂的产线平衡理论很有必要。
本文以实木A厂中的B产品作为研究对象,以Flexsim仿真建模与产线平衡率作为方法与参数对生产过程进行分析,将基础IE改善手法与0-1整数规划数学模型结合起来,对产线进行渐进性的改善,并最终达到企业的改善指标。
1 车间生产线现状分析
在当下竞争愈加激烈、追求低成本高利率的市场背景下,如何提升自身竞争力、成为家具行业的龙头企业,是A公司急需解决的问题。该厂是典型的传统制造型企业,且其产品类型为少批量多品种型,同时存在生产环境暗沉、加工设备老旧、工序之间出现频繁往返流、产品工艺路线不合理等问题,以上问题导致产能大幅度被减、人员与设备利用率低,严重影响生产效率。该厂主要生产办公用具如班台、文件柜等产品。在进行优化改善的过程中,本文选择了具有代表性的B型产品作为研究对象,该产品在市场上的需求大,代表性高,了解其生产流程,作出总工艺流程图,如图1所示。
A公司家具1号车间生产线是机群式生产,采用运输车进行部件运输,共有6道工序,分别是开料、加厚冷压、精裁、封边、排钻、锣铣磨。A公司家具生产线工位与工序时间相关信息如表1所示。

图1 B产品工艺流程图

表1 工序相关信息表
本文主要研究实木木工科生产线中的开料——试装的工艺流程,根据B型产品的生产工艺,经现场实地调研后作出该厂1号车间的位置布局图[2],如图2所示。
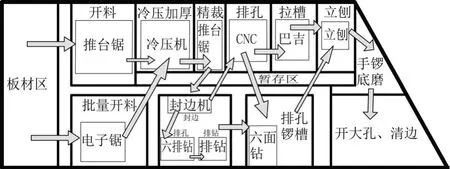
图2 1号车间现状布局图
通过现状布局图,可以发现以下问题:
(1)在整条生产线的布局中,木材板件的存放区域没有经过合理设计规划(只是简单的划分出区域),导致在生产过程中容易造成木材板件摆放混乱,增加操作者寻找时间,造成不必要的时间浪费。
(2)生产线缺乏统一、标准的现场管理。基本上都是由作业人员自行调配生产,操作动作、物料摆放等都是按照个人的习惯。生产时,很多操作动作都不符合动作经济原则,容易造成增加作业负荷、生产效率低下等问题。
(3)生产线中存在工序分配不均衡的问题,容易导致作业时间分配不均衡,造成部分操作者高负荷作业、部分操作者处于空闲状态。
2 生产线流程问题分析
2.1 建立Flexsim仿真模型
以A公司家具厂1号车间生产流程为依据,对应生产B型产品生产线中的12道工位,建立仿真模型,再将各个工位的生产时间输入Flexsim仿真模型,得到现状仿真图[3],如图3所示。按照1天8 h的标准工作时间运行软件,开料工序处理率为16.7%,而加厚冷压工序空闲率只有2.2%,可见生产线平衡率较差,瓶颈工序是加厚冷压,由上述仿真模型输出仿真数据分析表,如表2所示。
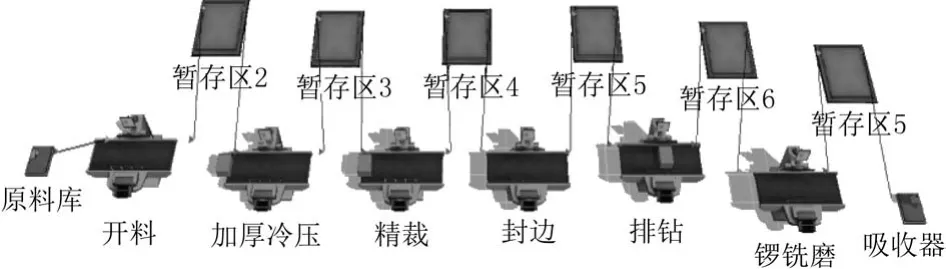
图3 现状仿真图

表2 仿真数据分析表
2.2 生产线平衡率分析
针对生产线平衡问题分析研究,常用生产线平衡率以及生产线平衡损失率来进行评价与比较。生产线平衡率P计算公式如下[4]:

式中:为所有工作站时间总和,根据上文收集数据计算工作站总时间和;C.Tmax为所有工序中最大工序作业时间;N为生产线工作站总和,则:

由上文计算的生产线平衡率为53.2%,远低于生产目标平衡率86%以上,造成生产线不平衡的原因是各工序的生产的速率不平衡,而各工序间的生产能力的不平衡,会导致各工序间的在制品的堆积等问题,造成等待浪费。
3 改善方案
3.1 方法步骤
第一步,基于ECRS的相关理论基础,先针对现状的瓶颈工序中的瓶颈工位结合动作分析进行改善,计算生产线的平衡率与目标平衡率对比;第二步,利用运筹学0-1整数规划建模分析的方法对工位进行重排,得出产线的平衡率再次与目标对比;第三步,若达到目标平衡率值,根据Lingo软件确定的工序进行Flexsim仿真建模评估,并对产线布局进行优化,若未达标,循环步骤一、二[5]。
3.2 基于ECRS原则的优化改善
由表1可知瓶颈工序为加厚冷压,其中时间最长的工位为钉框加厚,结合标准动作分析,利用ECRS原则对该工位进行改善,作出改善前后流程程序分析图,如表3、4所示。通过对动作进行重排、取消、合并,钉框加厚工位的搬运次数减少了两次,总时间由386.5 s缩短至308.5 s[6]。作出第一次瓶颈改善后数据分析表,如表5所示,经过第一次改善,总时间从1 728 s下降到1 650.3 s,缩短了77.7 s,生产平衡率从53.2%上升至59.41%,提高了6.21%。

表3 钉框加厚加工流程程序分析图(改善前)
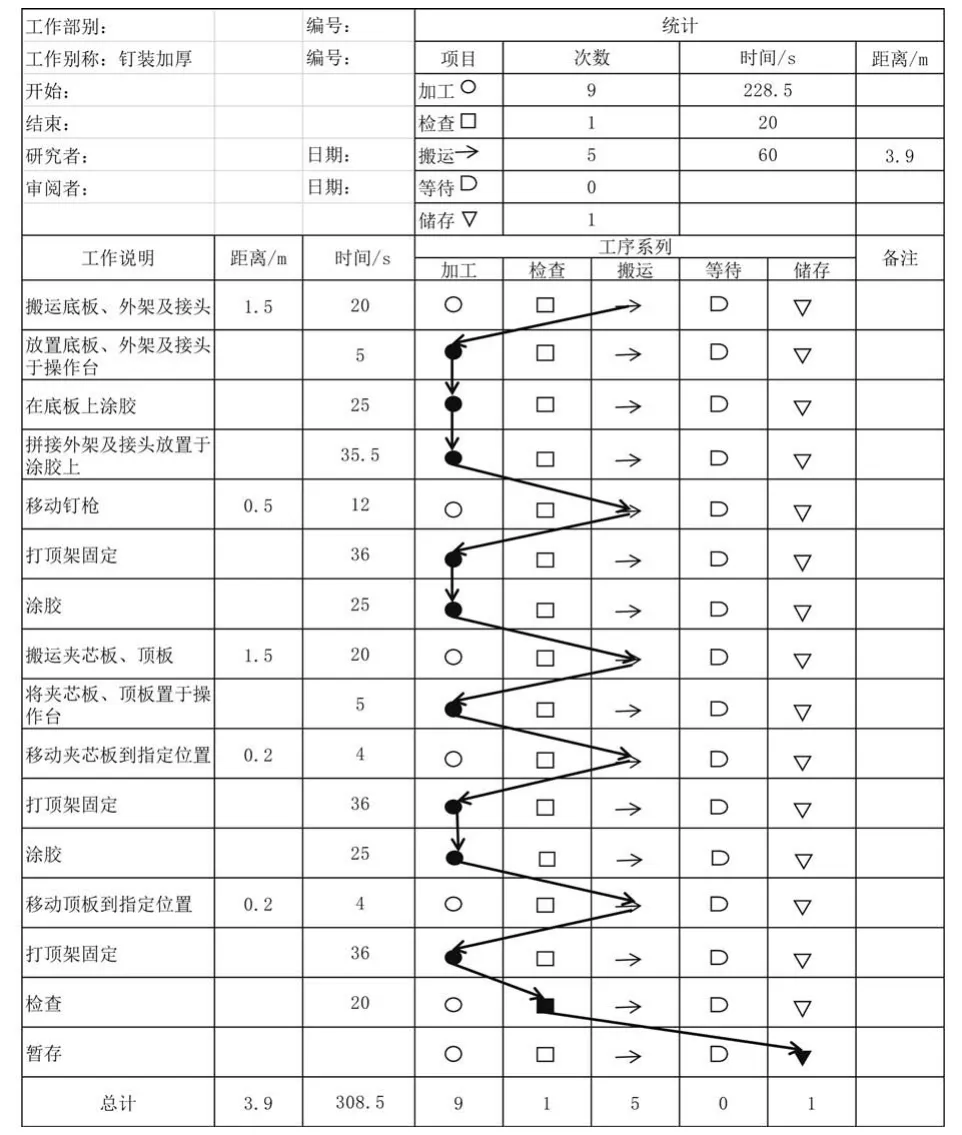
表4 钉框加厚加工流程程序分析图(改善后)

表5 第一次改善后数据分析表
3.3 基于0-1整数规划的优化改善
由于生产平衡率没有达到理想效果,因此进行第二次改善。第一步运用0-1整数规划的思想建立第二类生产线平衡问题的数学模型,第二步利用Lingo软件对其求解[7]。第一步,根据A厂现状情况,定义模型中所用到的变量与符号:
(1)符号定义如下:
CT为生产节拍;K为工序数目;k为工序序号,k=1,2,3,4…K;m为工位数目;i、j为工位的序号;Ti为第i个工位的作业时间,i=1,2,3,4…m;Pred为工位的优先关系的集合,Pred=({ i ,j)|工位i是j的上一道工位 } ;Tasks={1 ,2,3…m} ,表示工位集合。
(2)决策变量定义如下。
Xik:0-1变量;

Ak:工序k的指示变量。

其中,第二类问题中生产线工序数目(m)是固定的,在满足所有约束条件的前提下,使整个生产线的生产节拍CT最小化,Ti为工位的作业时间,其数学模型如下:
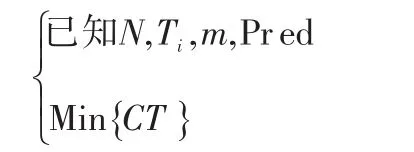
并设定约束条件如下。
(1)实木产品生产线中每个工位都必须分配到对应的工序上,其数学表达式为:
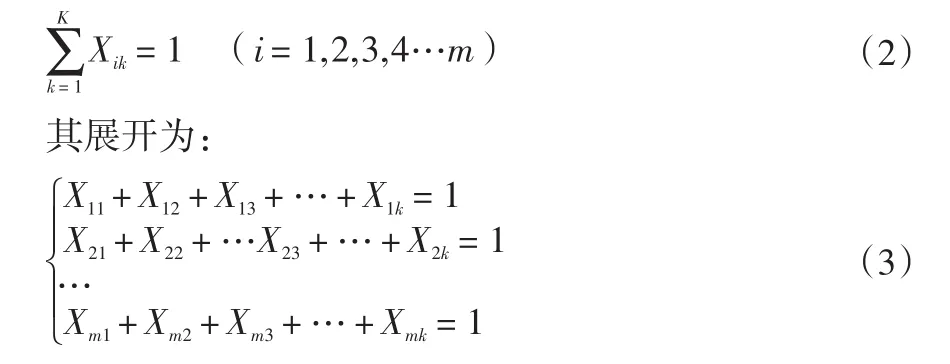
(2)实木产品生产线中,工位i为j的紧前作业,工位i一定是在工位j之前进行作业,即工位i只能分配到1~K工序中作业,而不能分配到其他工序中,其数字表达式为

(3)实木产品生产线中各个工序的作业时间总和必须小于生产节拍,其数字表达式为:
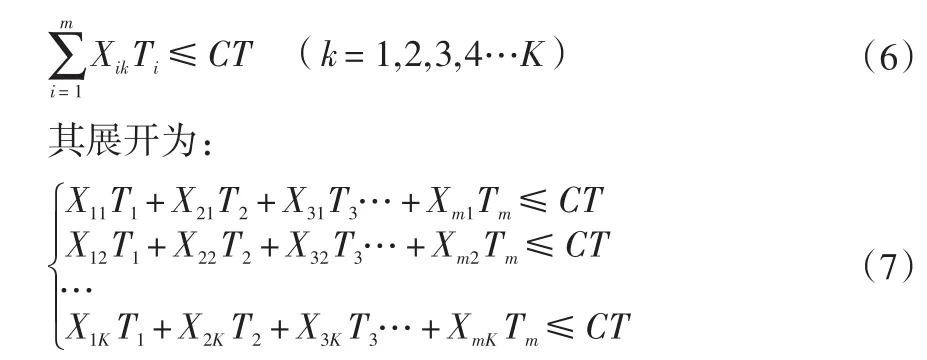
最后建立第二类实木生产线平衡问题的0-1整数规划模型如下[8]:

第二步,根据上述分析建立的第二类实木生产线平衡问题的0-1整数规划模型,将其转换为在LINGO软件中运行的目标函数[9],其中工位数目为:Task/1…12/:t;工位之间的关系以相应集合的表现形式为:Pred(Task,Task)/1,22,33,44,55,66,76,86,97,108,109,1010,1111,12/;工位的作业时间:DATA:T=91 154.5 386.5 79.3 180 165 92 87 68 48 168 209。
再按上述工艺流程图中工位时间和优先关系,根据LINGO软件的编程要求,编写第二类实木生产线平衡问题的0-1整数规划模型的LINGO程序,如图4所示。
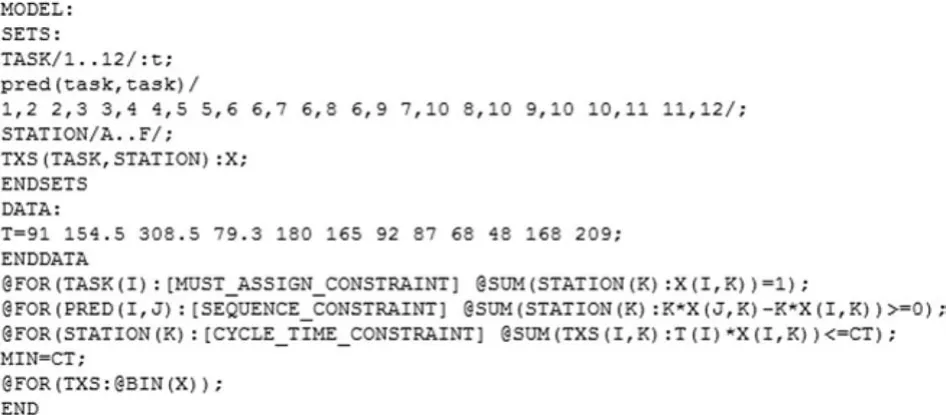
图4 求解模型代码
运行软件之后,以下分别得到模型LINGO求解的求解状态和求解报告[10],如图5、6所示。
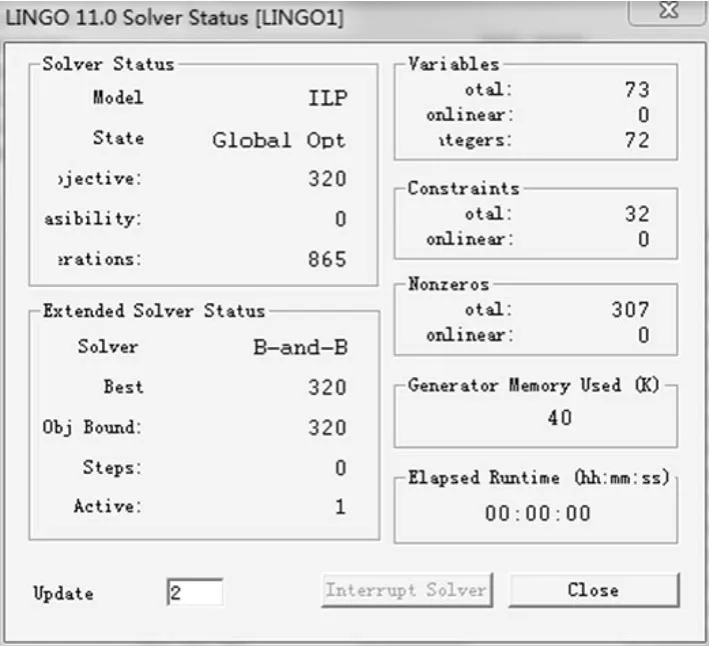
图5 求解状态

图6 求解报告
通过优化重排分配后结果如表6所示,当工序数M=6时,实木产线最小的生产节拍CT=320 s,其中生产平衡率提高至85%,但是仍然没有达到目标平衡率86%。
3.4 基于人机作业表的优化改善
对上述重排后产线的工序进行分析,绘制了工序时间直方图,如图7所示。又由直方图,可知瓶颈工序是四号工序,而四号工序中封边工位时间最长,为165 s,由此绘制人机作业表对其进行作业分析再次进行优化改善,如表7所示。
由人机作业分析表,并运用ECRS原则,对操作者与机器之间的关系进行优化改善[6],工位时间由原来的165 s降到156 s。结合改善结果和重排之后的工位顺序,绘制了第二次瓶颈改善数据分析表,如表8所示。经过第二次改善,最终生产平衡率达到87.9%,超过目标的生产平衡率达到了预期目标。
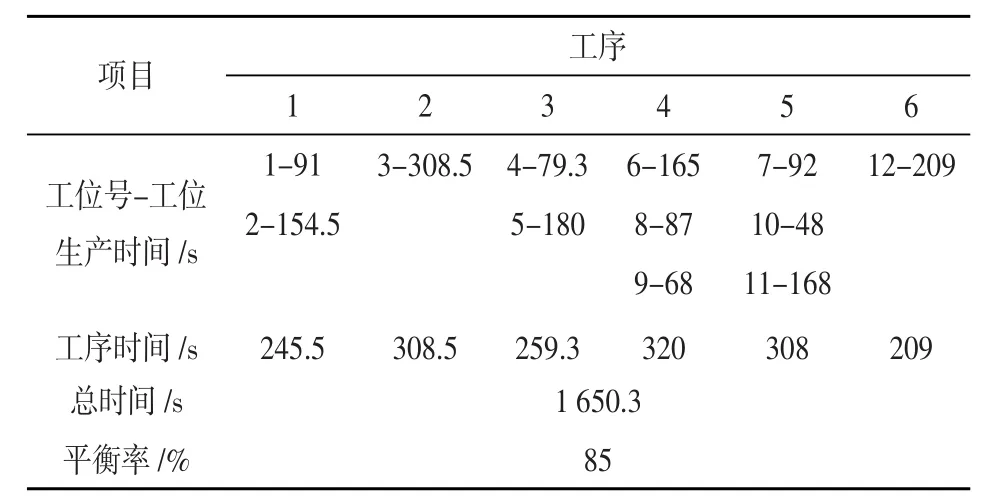
表6 0-1整数规划改善后数据分析表
3.5 改善后Flexsim建模分析
为了验证生产线的改善效果,所以需要建立新的仿真模型,并且输出了新的仿真数据,如图8、表9所示。从表9可见,每道工序处理率相对于原来的现状有了极大的提升,空闲率得到有效的降低,并且每个工序的生产处理率更平衡了。

图7 工序时间直方图
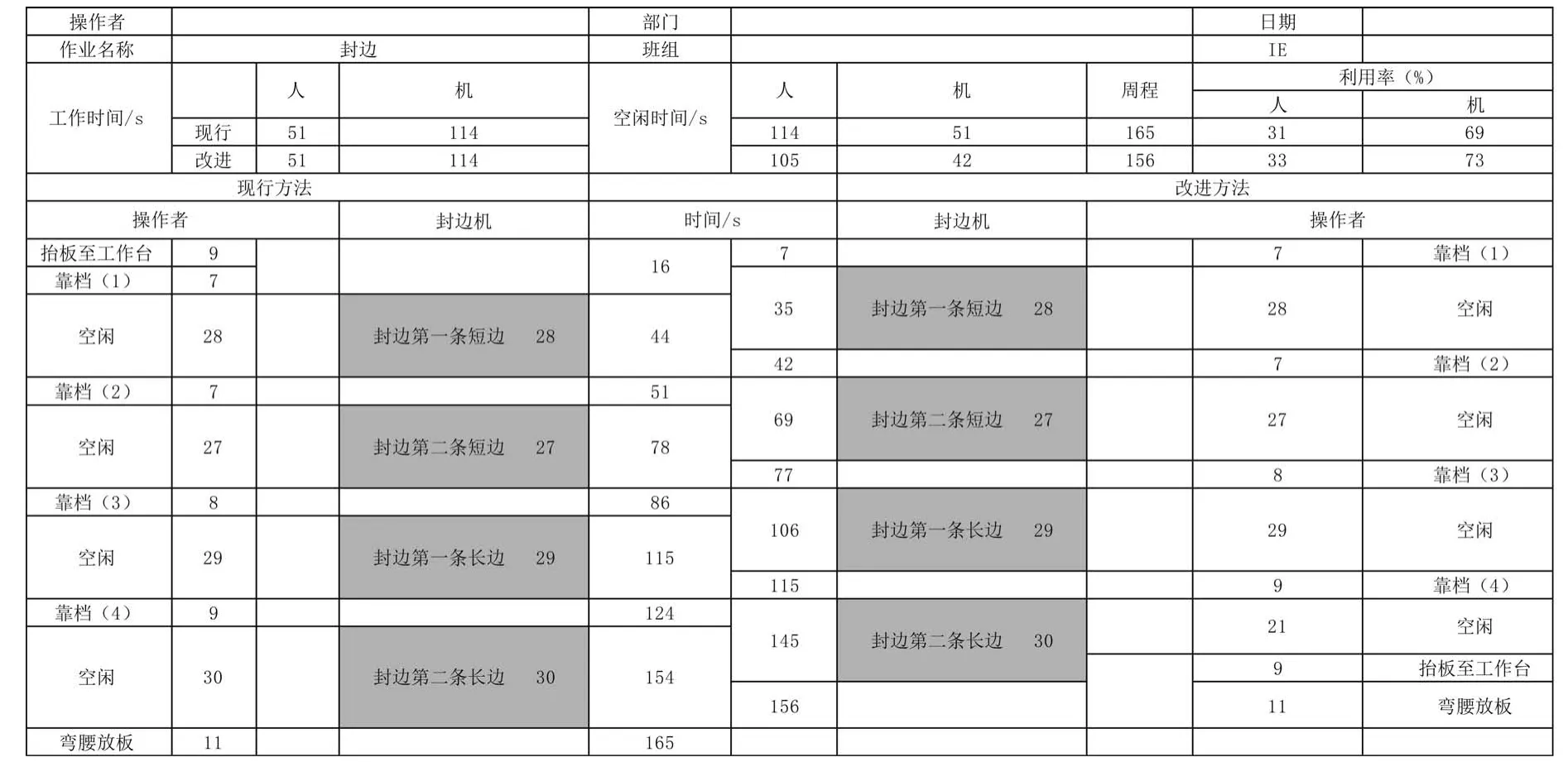
表7 封边工序人机作业表

表8 第二次瓶颈改善数据分析表
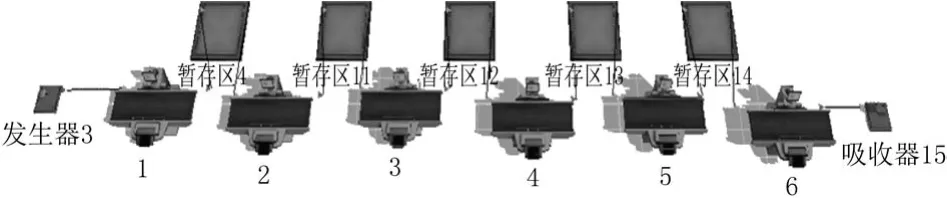
图8 改善后的仿真模型分析

表9 仿真数据分析表

图9 改善后实木A厂1号车间布局设计
3.6 改善后布局优化
根据0-1整数规划模型和Lingo软件算出的工序排序,得到最优的生产节拍和平衡率,并重新规划了实木A厂1号车间的布局,如图9所示。重新规划布局后的1号车间,将大批量生产的产品与多品种小批量的产品流过涉及设备与手工作业的工位分开两条线布置,减少了生产时在制品的回流现象,布局上更合理化[11]。
4 结束语
本文研究结果说明了传统IE结合运筹学,并运用Lin⁃go进行运算,能够很好地解决机群式的家具生产问题。传统IE手段用于解决瓶颈工序问题,使1号车间生产线总时间减少了87 s,运筹学结合Lingo解决了生产线平衡问题,使生产线平衡率达到86%以上,为解决家具生产问题提供了理论参考依据。

