一种改进的基于Gabor小波的人脸识别方法

罗 敏 ，刘 嵩 ，刘利平 ，李时东，张国平

（1.华中师范大学 物理科学与技术学院，武汉 430079；2.湖北民族学院 理学院，湖北 恩施 445000；3.湖北民族学院 信息工程学院，湖北 恩施 445000）

人脸识别是模式识别和计算机视觉领域的热点，有着重大的理论研究价值和广泛的实践应用前景.目前受人脸姿态、光照等不利因素的影响，人脸识别性能还尚待提高，而Gabor特征对光照、表情和姿态造成的局部变化具有良好的鲁棒性，引起了研究人员的关注，并取得了一定的成果［1－2］.Lades和Vorbruggen等人作出了开创性的工作，首次将Gabor小波变换用于人脸识别［3］.

Wiskott等人利用人脸的基准特征点构造拓扑图，提出了弹性约束图匹配算法［4］.Liu 和Wechsler利用Fisher线性判别模型对Gabor特征进行进一步的提取和分类［5］.

Gabor小波应用于人脸识别优点在于：

1）Gabor小波准确逼近简单细胞的感受野，在很大程度上反应了人脸的不变信息；2）Gabor小波是唯一能够达到时域测不准下界的函数，它能够最好地兼顾信号在时域和频域中的分辨能力，可以捕获人脸图像在不同频率和不同方向下的局部特征，很好表达了人脸特征［6］.而Gabor小波提取特征在本质上是通过一系列多尺度、多方向的滤波器组，分别和人脸图像作卷积.例如对于一张大小为112×92 的人脸图像，使用Gabor 小波提取特征，当使用的尺度和方向个数分别为5和8时，Gabor小波得到的特征就是通过40个滤波器与图像卷积得到，特征维数为112×92×5×8＝412160.可以看出，Gabor小波获取的特征维数都很高，并且一定存在大量不利于分类识别的冗余信息，相应的也增加了算法的时间复杂度和空间复杂度.因此改善Gabor小波变换算法的性能是亟待解决的问题.

代数特征体现了图像的本质属性，奇异值分解（Singular Value Decomposition∶SVD）为提取图像代数特征提供了新的方法.研究表明SVD 用于人脸识别不仅可以降低识别的存储开销，还可以通过快速算法减少识别时间开销［7－8］.Hong还证明了SVD 具有旋转不变性、平移不变性、镜像不变性和稳定性［9］.受以上启发，提出了一种改进的基于Gabor小波的人脸识别算法，该算法将SVD 融合于Gabor的方法中，实验证明了该算法的有效性.

1 算法原理

1.1 Gabor小波变换

二维Gabor小波是经高斯函数调制的正弦栅格，在频域上表现为一种带通滤波器，且主频和方向可调.二维Gabor小波的定义为［10］［11］：

人脸图像的Gabor小波变换就是人脸图像矩阵与Gabor小波的卷积：

1.2 奇异值分解SVD

定理1 奇异值分解［13］设Αm×n是实矩阵（不失一般性，设m≥n），且rank（）Α＝k，则存在两个正交矩阵Um×m和Vn×n及对角阵Dm×n使下式成立：

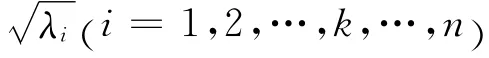
设A表示一图像矩阵，根据定理1，A可按下式分解

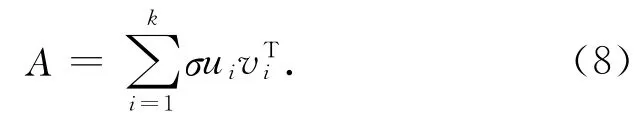
图1 图像重构Fig.1 The reconstructed image

2 本文算法

本文提出的改进的Gabor小波算法流程图如图2所示，具体描述如下.

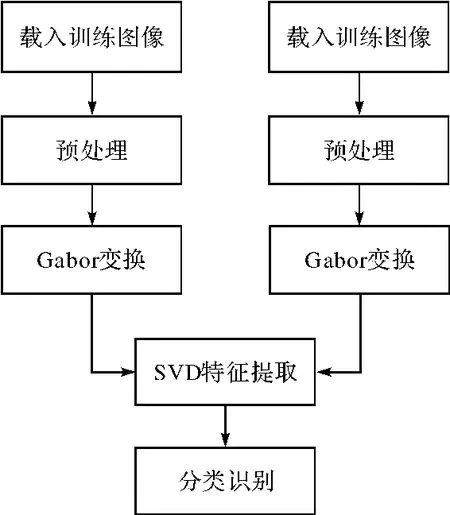
图2 算法流程图Fig.2 Flow diagram of arithmetic

1）对训练图像和测试图像进行预处理.预处理可以改善图像质量，消除不利于分类的因素.本文算法的预处理过程包括图像平滑和灰度归一化.图像平滑采用邻域平均法实现，也即用像素邻域内各像素的灰度平均值代替该像素原来的灰度值.灰度归一化通过灰度变换将图像的灰度分布的均值和均方差统一调整到预定的数值，采用的灰度变换如下：

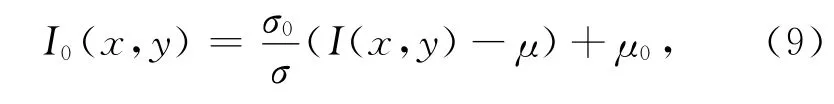
其中，I0（x，y），μ0，σ0分别为变换后的灰度值、均方差、均值，I（x，y），μ，σ分别为变换前的灰度值、均方差、均值.

3）SVD 提取特征.首先将测试集的Gabor特征图像按公式（3）进行奇异值分解，获取测试样本的奇异值特征和基空间.然后将训练集的Gabor特征图像投影到基空间，获取在同一基空间的奇异值.最后将提取的两个样本集的奇异值特征按尺度和方向由小到大的顺序排列成列向量构成融合特征.

4）分类识别.采用最近邻分类器对提取的特征进行分类，特征间的距离度量采用欧氏距离，距离最近者判决为同一类.

3 实验结果及分析

为了验证本文方法的有效性，在ORL人脸数据库上进行了相关实验.ORL数据库的每幅图像大小为92×112，由40个人，每人10幅、共400幅.这些人脸图像分别是在不同光照、不同姿态和不同表情条件下摄制而得，是目前使用最广泛的标准图像.实验的平台环境：MATLAB 7.6，处理器E2210，内存3G.为了提高识别结果的精确性，每一个实验都重复20次，最后取20次实验结果的平均.

实验中首先比较了Gabor小波方法和本文改进的Gabor小波方法的性能.在实验中随机抽取ORL库中的每人5 幅图像作为训练样本，余下5幅图像作为测试样本，这样训练样本集和测试样本集总数均为200，奇异值分解的基空间维数为5.图3给出了不同的尺度和方向条件下两种方法的识别率对比.从图3可以看出，本文方法的识别率明显高于单一的Gabor方法，说明本文方法能够提取更有鉴别力的特征.

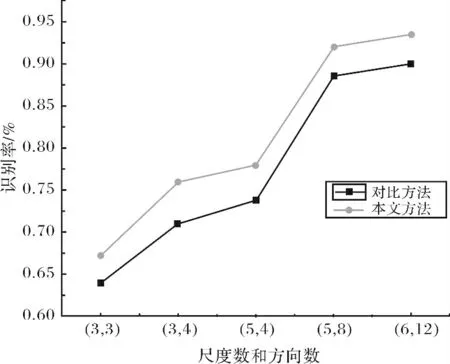
图3 不同的尺度和方向条件下两种方法的识别率Fig.3 Comparison in terms of recognition rate

图4给出了不同的尺度和方向条件下两种方法的训练时间和识别时间对比.从图4可以看出，增加Gabor变换尺度、方向的数量可以提高人脸识别率，但数量的增加也导致了算法时间开销和存储开销的增加.从算法实用性的角度考虑，算法复杂度是考量一个算法好坏与否的重要标准.本文方法相当于采用了奇异值分解对鉴别特征进行压缩，因此节约了大量内存单元，空间复杂度改善很明显.人脸识别时间包括训练时间和测试时间，而在实际应用中，训练一般采用离线训练的方法，训练时间对算法的实时性并无影响，因而算法的时间复杂度主要取决于分类时间.由于本文方法在训练阶段增加了奇异值分解的过程，所以与传统方法比训练时间都增加了.但是在测试阶段，由于本文方法采用SVD 的方法对特征图像降维，减小了算法的分类时间，改善了算法的时间复杂度，特别是在尺度和方向较多的条件下，这种改善更为明显.结合实验情况，综合考虑选择5个尺度8 个方向共40个小波参入特征提取，能够使本文算法的综合性能达到最优，此时识别率可以达到92%，而分类时间为18.5s，缩短了5.5s.

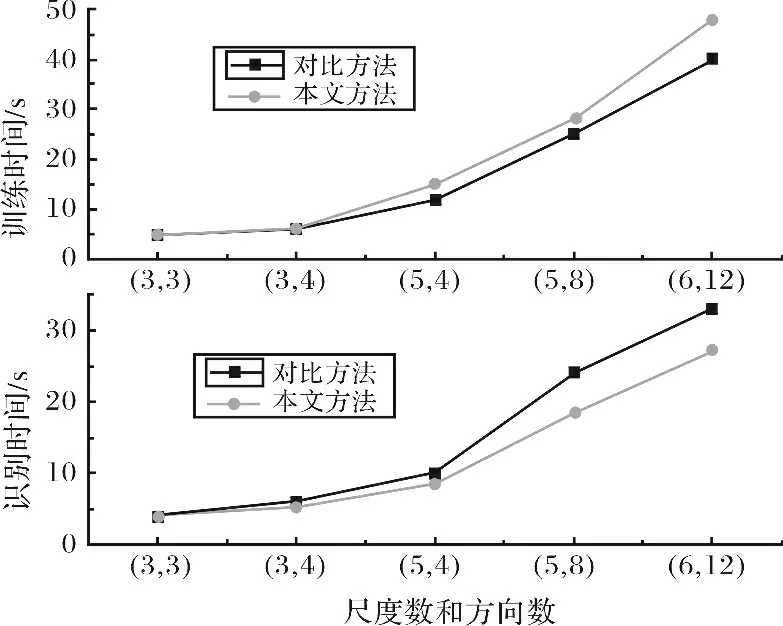
图4 不同的尺度和方向条件下两种方法的训练时间和识别时间对比Fig.4 Comparison in terms of recognition time

实验中还研究了样本数目和基空间维数对本文算法的影响.Gabor小波的尺度和方向按前述最优值分别为5、8.首先设置基空间维数为5，测试样本数目对算识别率的影响，实验结果如表1所示.然后交换前述实验的训练集和测试集，改变基空间维数，测试算法性能，实验结果如表2所示.

表1 样本数目对识别率的影响Tab.1 Influence of samples number in terms of recognition rate

表2 基空间维数对算法的影响Tab.2 Influence of base－space dimensions in terms of recognition performance

从表1可以看出，样本数目越多，算法的识别率越高，与理论结果完全一致.从表2可以看出，随着基空间维数增加，算法的识别率也是增加的，当增加到一定程度后，人脸识别率趋于稳定，说明已经提取了绝大部分鉴别特征了，舍弃的部分作用不是特别大.但是基空间维数增加，特征维数和识别时间迅速增加，考虑综合性能，基空间的维数选择5比较合适.

4 结束语

本文提出了一种改进的Gabor小波变换的人脸识别方法，该方法充分利用了Gabor 小波和SVD 各自的优势，实验结果证明本文方法改善了Gabor小波变换方法的性能.然而Gabor小波变换用于人脸识别的实时性还没有根本解决，这将是进一步研究的重点.

［1］张文超，张洪明.基于局部Gabor变化直方图序列的人脸描述与识别［J］.软件学报，2006，17（12）：2508－2517.

［2］Zhao San－qiang，Gao Yong－sheng，Zhang Bao－chang.Gabor feature constrained statistical model for efficient and mark localization and face recognition［J］.Pattern Recognition Letters，2009，30（10）：922－930.

［3］Lades M，Vorbruggent J C，et al.Distortion invariant object recognition in the dynamic Link architecture［J］.IEEE Trans On Computers，1993，42（3）：300－311.

［4］Wiskott L，Fellous J M，Krugen N，et al.Face recognition by elastic bunch graph matching［J］.IEEE Trans on PAMI，1997，19（7）：775－779

［5］Liu C，Wechsler H.Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition［J］.IEEE Transactions on Image Processing，2002，11（4）：467－476.

［6］陈 洋，王润生.结合Gabor滤波器和ICA 技术的纹理分类方法［J］.电子学报，2007，35（2）：299－302.

［7］王宏勇，廖海斌，段新华.基于奇异值与特征融合矩阵的自适应人脸识别［J］.计算机工程与应用，2010，46（7）：162－174.

［8］张新征.基于多小波子带加权判别熵的SAR 目标ICA 特征提取及识别［J］.计算机应用，2011，31（9）：2468－2471.

［9］Hong Z Q.Algebraic feature extraction of image for recognition［J］.Pattern Recognition，1991，24（3）：211－219.

［10］顼改燕，徐 华，翟忠武.基于Gabor滤波器和BP神经网络的人脸皮肤皱纹区域自动识别［J］.计算机应用，2010，30（2）：430－432.

［11］时书剑，马 燕.基于Gabor滤波和KPCA 的人脸识别方法［J］.计算机技术与发展，2010，20（4）：51－57.

［12］鲍丽山，何光辉.Gabor变换仿生人脸识别［J］.计算机应用，2010，30（1）：166－168.

［13］高全学，梁 彦，潘 泉.SVD 用于人脸识别存在的问题及解决方法［J］.中国图象图形学报，2006，12（11）：1785－1791.